In which of the following cases the heavier of the two particles has a smaller de-Broglie wavelength ? The two particles
move with the same speed
move with the same linear momentum
move with the same kinetic energy
have fallen through the same height
The correct Answer is:A, C, D
To determine in which case the heavier of the two particles has a smaller de-Broglie wavelength, we will analyze each of the given scenarios step by step.
Given Options:
1. Particles move with the same speed.
2. Particles move with the same linear momentum.
3. Particles move with the same kinetic energy.
4. Particles have fallen to the same height.
Step 1: De-Broglie Wavelength Formula
The de-Broglie wavelength (λ) is given by the formula:
λ=hmv
where h is Planck's constant, m is the mass of the particle, and v is its velocity.
Step 2: Analyze Each Case
Case 1: Particles move with the same speed
- Let the mass of particle X (heavier) be mx and the mass of particle Y (lighter) be my.
- Since both particles move with the same speed v:
λx=hmxvandλy=hmyv
- Since mx>my, it follows that:
λx<λy
Thus, the heavier particle (X) has a smaller de-Broglie wavelength. (This case is correct)
Case 2: Particles move with the same linear momentum
- Linear momentum p is given by p=mv.
- If both particles have the same momentum:
mxvx=myvy
- Rearranging gives:
vx=mymxvy
- Substituting vx and vy into the de-Broglie wavelength equations:
λx=hmxvxandλy=hmyvy
- Since mxvx=myvy, we find:
λx=λy
Thus, the heavier particle does not have a smaller wavelength in this case. (This case is incorrect)
Case 3: Particles move with the same kinetic energy
- Kinetic energy K is given by:
K=12mv2
- If both particles have the same kinetic energy:
12mxv2x=12myv2y
- Rearranging gives:
mxv2x=myv2y
- Using the de-Broglie wavelength formula:
λx=hmvandλy=hmv
- We can derive that the heavier particle will have a smaller wavelength:
λx<λy
Thus, the heavier particle (X) has a smaller de-Broglie wavelength. (This case is correct)
Case 4: Particles have fallen to the same height
- When falling from the same height h, both particles gain the same potential energy which converts to kinetic energy:
mgh=12mv2
- Since both particles fall the same height, they will have the same velocity:
vx=vy
- Therefore, using the de-Broglie wavelength formula:
λx=hmxvandλy=hmyv
- Since mx>my:
λx<λy
Thus, the heavier particle (X) has a smaller de-Broglie wavelength. (This case is correct)
Conclusion:
The correct options where the heavier particle has a smaller de-Broglie wavelength are:
- Case 1: Particles move with the same speed.
- Case 3: Particles move with the same kinetic energy.
- Case 4: Particles have fallen to the same height.
Final Answer:
The heavier of the two particles has a smaller de-Broglie wavelength in cases 1, 3, and 4.
---
1. Particles move with the same speed.
2. Particles move with the same linear momentum.
3. Particles move with the same kinetic energy.
4. Particles have fallen to the same height.
The de-Broglie wavelength (λ) is given by the formula:
λ=hmv
where h is Planck's constant, m is the mass of the particle, and v is its velocity.
- Let the mass of particle X (heavier) be mx and the mass of particle Y (lighter) be my.
- Since both particles move with the same speed v:
λx=hmxvandλy=hmyv
- Since mx>my, it follows that:
λx<λy
Thus, the heavier particle (X) has a smaller de-Broglie wavelength. (This case is correct)
- Linear momentum p is given by p=mv.
- If both particles have the same momentum:
mxvx=myvy
- Rearranging gives:
vx=mymxvy
- Substituting vx and vy into the de-Broglie wavelength equations:
λx=hmxvxandλy=hmyvy
- Since mxvx=myvy, we find:
λx=λy
Thus, the heavier particle does not have a smaller wavelength in this case. (This case is incorrect)
- Kinetic energy K is given by:
K=12mv2
- If both particles have the same kinetic energy:
12mxv2x=12myv2y
- Rearranging gives:
mxv2x=myv2y
- Using the de-Broglie wavelength formula:
λx=hmvandλy=hmv
- We can derive that the heavier particle will have a smaller wavelength:
λx<λy
Thus, the heavier particle (X) has a smaller de-Broglie wavelength. (This case is correct)
- When falling from the same height h, both particles gain the same potential energy which converts to kinetic energy:
mgh=12mv2
- Since both particles fall the same height, they will have the same velocity:
vx=vy
- Therefore, using the de-Broglie wavelength formula:
λx=hmxvandλy=hmyv
- Since mx>my:
λx<λy
Thus, the heavier particle (X) has a smaller de-Broglie wavelength. (This case is correct)
The correct options where the heavier particle has a smaller de-Broglie wavelength are:
- Case 1: Particles move with the same speed.
- Case 3: Particles move with the same kinetic energy.
- Case 4: Particles have fallen to the same height.
The heavier of the two particles has a smaller de-Broglie wavelength in cases 1, 3, and 4.
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Exercise
35 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective I
14 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
Knowledge Check
Which of these particles having the same kinetic energy has the largest de Broglie wavelength ?
AElectronBAlpha particleCProtonDNeutronWhich of the following figure represents the variation of particle momentum and the associated de - Broglie wavelength ?
A B
B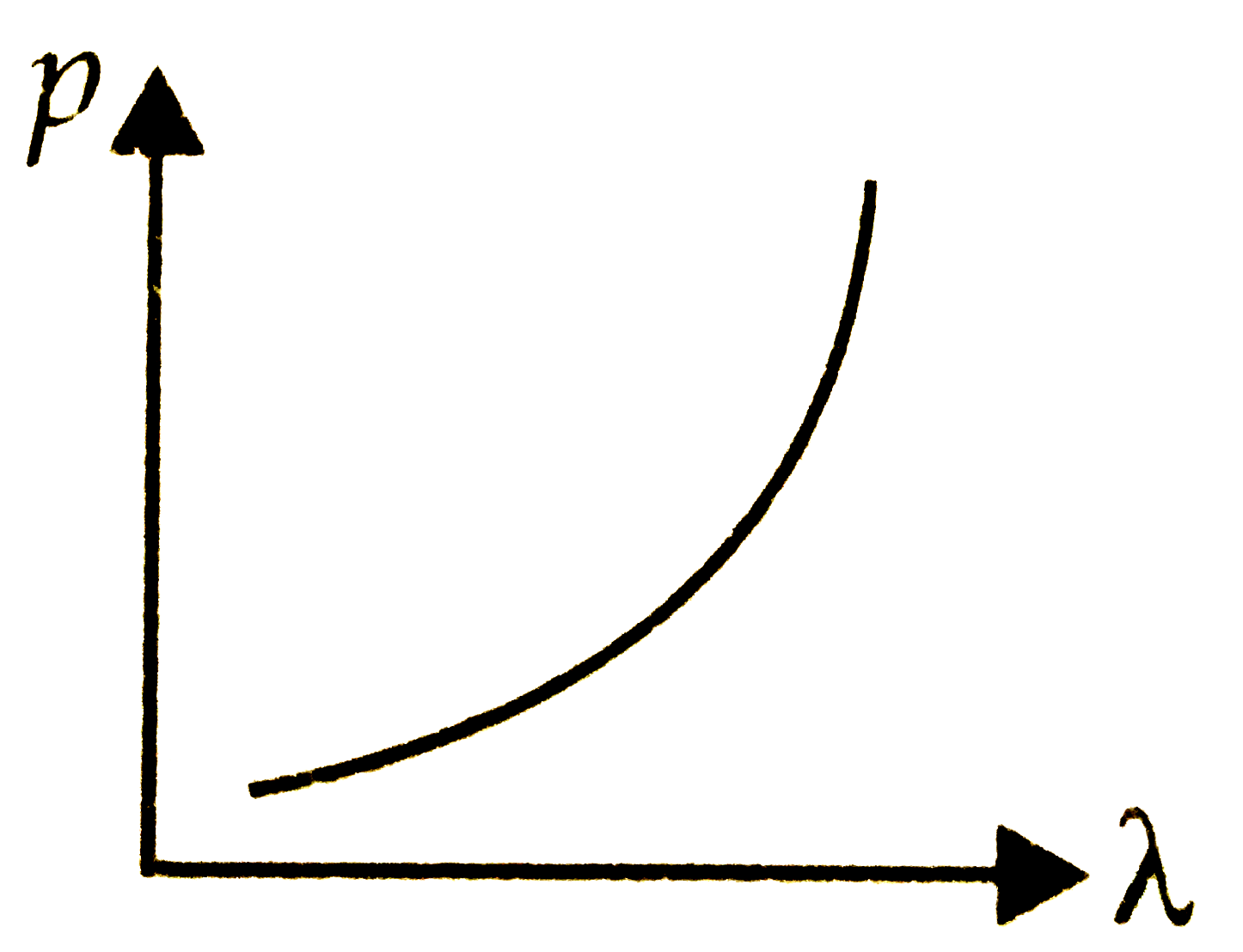 C
C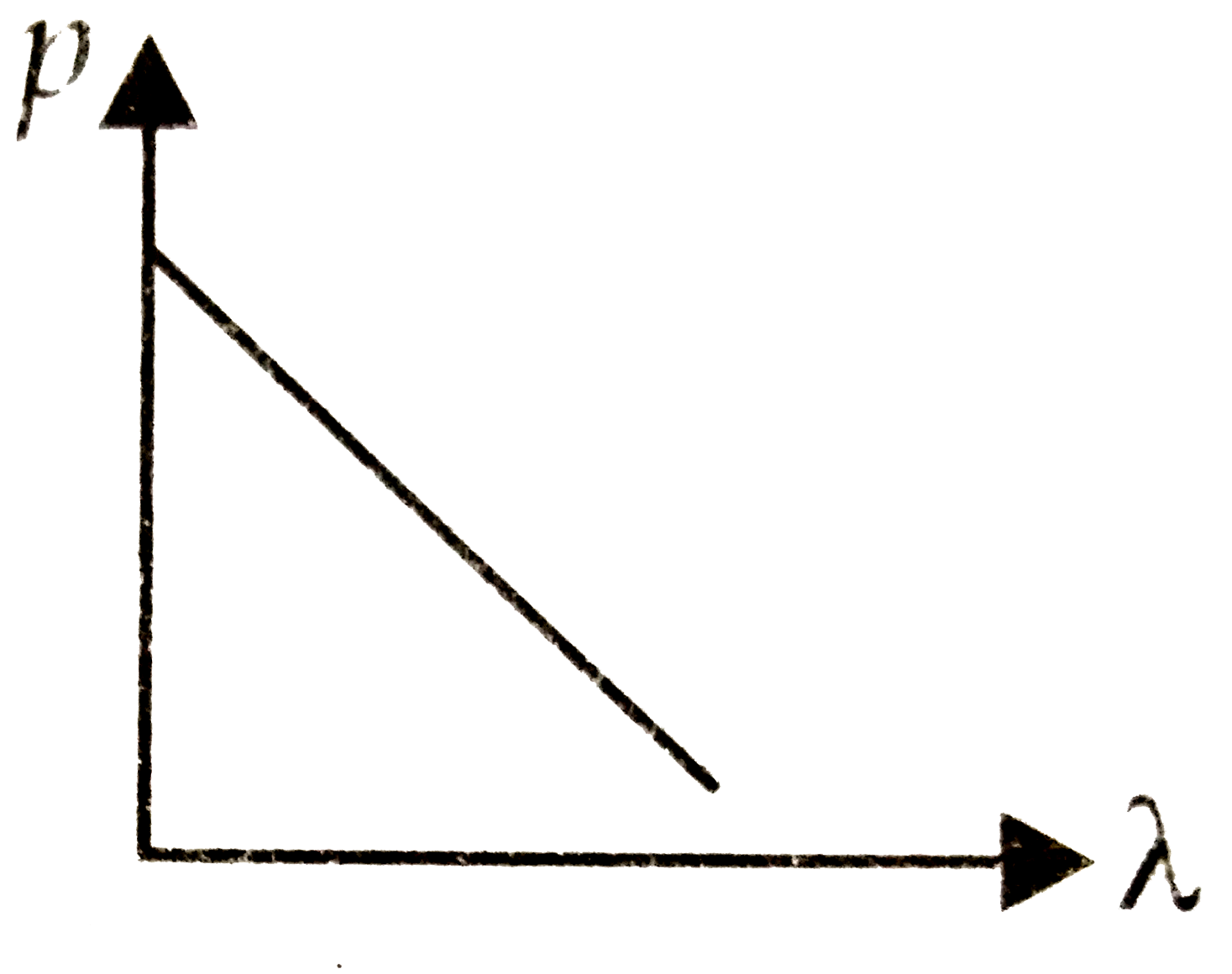 D
D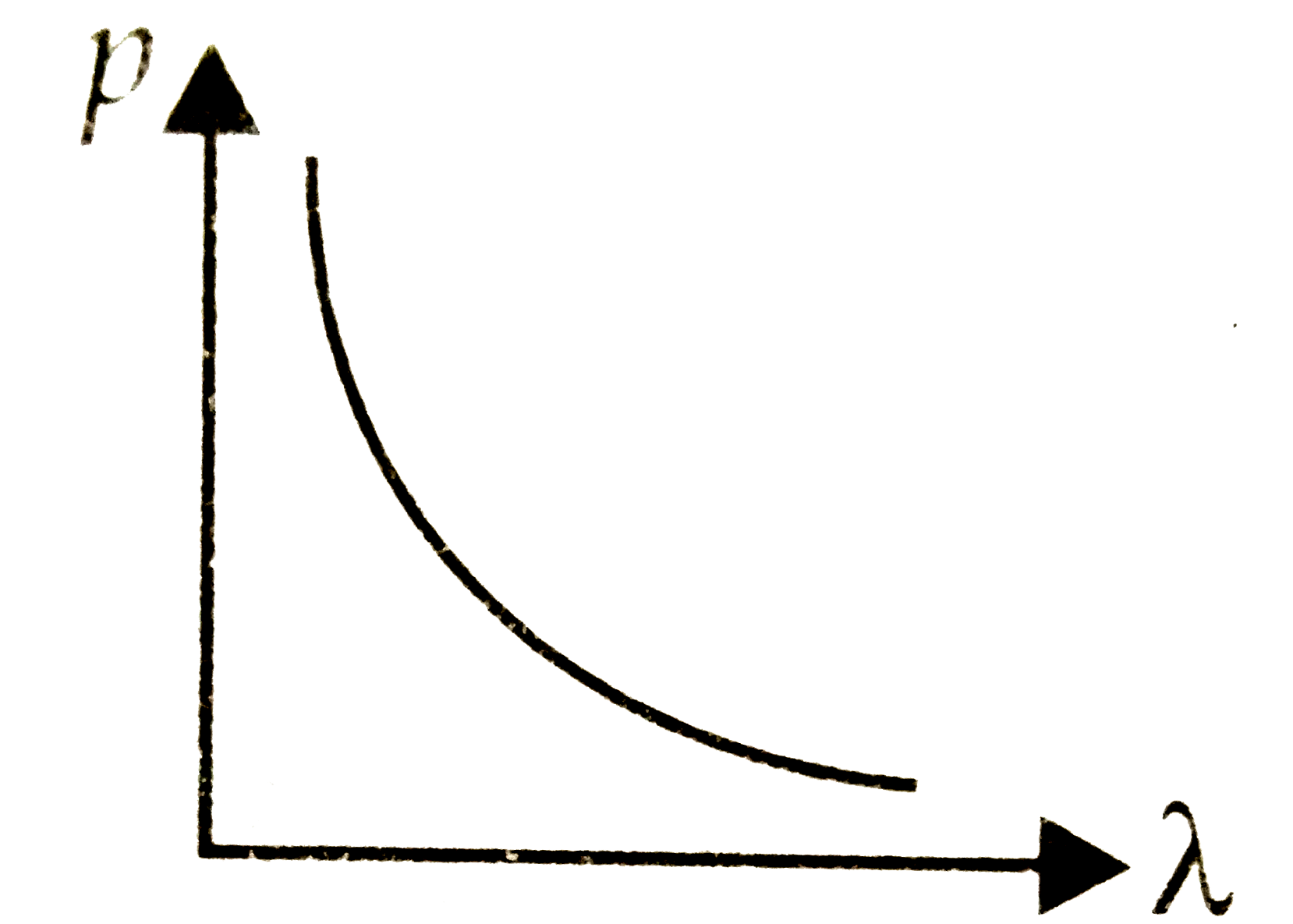
For particles having same K.E., the de-Broglie wavelength is
View SolutionThe momentum of a particle associated with de-Broglie's wavelength of 6Å is
View SolutionIf the kinetic energy of a moving particle is E , then the de-Broglie wavelength is
View SolutionFor a given kinetic energy, which of the following has the smallest de Broglie wavelength : electron, proton and α−partic≤?
View SolutionIn which of the following conditions the de Broglie wavelength of particle A will be less than that of particle B(mA>mB)?
View SolutionCalculate the momentum of a particle which has de Broglie wavelength of 0.1 nm.
View Solution
