A beam of light having wavelength distributed uniformly between 450nm→550nm passes through a sample of hydrogen gas which wavelength will have the least intensity in the transition beam?
The correct Answer is:D
To solve the problem, we need to determine which wavelength of light will have the least intensity after passing through a sample of hydrogen gas. The light beam has a wavelength range of 450 nm to 550 nm, and we will analyze the energy transitions in hydrogen to find the wavelength that corresponds to the least intensity.
1. Identify the Wavelength Range:
The given wavelength range of the light beam is from 450 nm to 550 nm.
2. Calculate the Energy for Minimum Wavelength (450 nm):
The energy associated with a wavelength can be calculated using the formula:
E=hcλ
Where:
- h (Planck's constant) = 4.1357×10−15 eV·s
- c (speed of light) = 3×108 m/s
- λ = 450 nm = 450×10−9 m
Substituting the values:
E1=1242450≈2.76 eV
3. Calculate the Energy for Maximum Wavelength (550 nm):
Using the same formula for the maximum wavelength:
E2=1242550≈2.25 eV
4. Determine the Energy Range:
The energy range of the light beam is from E2 to E1:
ΔE=E1−E2=2.76 eV−2.25 eV=0.51 eV
5. Identify the Transitions in Hydrogen:
For hydrogen, the energy levels are given by:
En=−13.6n2 eV
The transitions that can occur are from higher energy levels (n = 3, 4, 5, ...) to n = 2 (the first excited state).
6. Calculate Energy Differences for Transitions:
- Transition from n=3 to n=2:
E3→2=E2−E3=13.6(122−132)=13.6(14−19)≈1.89 eV
- Transition from n=4 to n=2:
E4→2=E2−E4=13.6(122−142)=13.6(14−116)≈2.55 eV
- Transition from n=5 to n=2:
E5→2=E2−E5=13.6(122−152)=13.6(14−125)≈2.85 eV
7. Identify the Wavelength Corresponding to the Least Intensity:
The transition with the least intensity will correspond to the energy that falls within the range of 2.25 eV to 2.76 eV. The transition from n=4 to n=2 gives us:
E=2.55 eV
Now, we convert this energy back to wavelength:
λ=12422.55≈487 nm
8. Conclusion:
The wavelength that will have the least intensity in the transition beam is approximately 487 nm.
The given wavelength range of the light beam is from 450 nm to 550 nm.
The energy associated with a wavelength can be calculated using the formula:
E=hcλ
Where:
- h (Planck's constant) = 4.1357×10−15 eV·s
- c (speed of light) = 3×108 m/s
- λ = 450 nm = 450×10−9 m
E1=1242450≈2.76 eV
Using the same formula for the maximum wavelength:
E2=1242550≈2.25 eV
The energy range of the light beam is from E2 to E1:
ΔE=E1−E2=2.76 eV−2.25 eV=0.51 eV
For hydrogen, the energy levels are given by:
En=−13.6n2 eV
The transitions that can occur are from higher energy levels (n = 3, 4, 5, ...) to n = 2 (the first excited state).
- Transition from n=3 to n=2:
E3→2=E2−E3=13.6(122−132)=13.6(14−19)≈1.89 eV
- Transition from n=4 to n=2:
E4→2=E2−E4=13.6(122−142)=13.6(14−116)≈2.55 eV
- Transition from n=5 to n=2:
E5→2=E2−E5=13.6(122−152)=13.6(14−125)≈2.85 eV
The transition with the least intensity will correspond to the energy that falls within the range of 2.25 eV to 2.76 eV. The transition from n=4 to n=2 gives us:
E=2.55 eV
Now, we convert this energy back to wavelength:
λ=12422.55≈487 nm
The wavelength that will have the least intensity in the transition beam is approximately 487 nm.
Topper's Solved these Questions
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMA ENGLISHChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Short Answer
Explore 10 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMA ENGLISHChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Obejective - II
Explore 5 Videos
- ALTERNATING CURRENTBook:HC VERMA ENGLISHChapter:ALTERNATING CURRENTExercise:Short answer
Explore 14 Videos
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:short answer
Explore 7 Videos
Similar Questions
In this problem , which wavelength (s) will have a strong intensity if light have wavelength 400 nm-700 nm?

View SolutionA beem of ultraviolet radius hacking wavelength between 100nmand200nm is inclined on a sample of atomic hydrogen gos Assuming that the atoms are in ground state which wavelength will have low intensity in the transnilled been? If the energy of a photon is equal to the ground state it haslarge probobility of being observed by on atom in the ground state
View SolutionA beam of ultraviolet light of all wavelength passes through hydrogen gas at room temperature, in the x-direction. Assume that all photons emitted due to electron transitions inside the gas emerge in the y-direction. Let A and B denote the lights emerging from the gas in the x-and y-directions respectively.
(i) Some of the incident wavelengths will be absent in A
(ii) Only those wavelengths will be present in B which are absent in A
(iii) B will contain some visible light
(iv) B will contain some infrared light
View SolutionA monochromatic beam of light having photon energy 12.5eV is incident on a simple A of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample B of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The atoms of sample A after passing of light through it
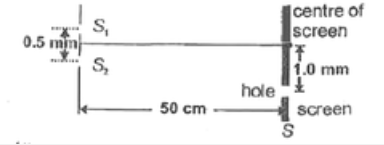
View SolutionIn young's double slit experiment shown in figure, S1andS2 are coherent sources and S in the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
View SolutionA monochromatic beam of light having photon energy 12.5eV is incident on a simple A of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample B of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The atoms of sample B
View SolutionA monochromatic beam of light having photon energy 12.5eV is incident on a simple A of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample B of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The emission spectra of sample A
View SolutionWhite light is a mixture of light of wavelengths between 400 nm and 700 nm. If this light goes through water (μ=1.33) what are the limits of the wavelength there ?
View SolutionA parallel beam of light of wavelength λ passes through a slit of width d. The transmitted light is collected on a screen D aways (D>>d). Find the distance between the two second order minima.
View SolutionA neutron beam, in which each neutron has same kinetic energy, is passed through a sample of hydrogen like gas (but not hydrogen) in ground state and at rest. Due to collision of neutrons with the ions of the gas, ions are excited and then they emit photons. Six spectral lines are obtained in which one of the lines is of wavelength (6200/51) nm.Which gas is this?
View Solution