Write the truth table for the logical function Z=(X and Y)or X.
To write the truth table for the logical function Z=(X∧Y)∨X, we will follow these steps:
Step 1: Identify the Variables
The variables involved in the function are X and Y. Each variable can take a value of either 0 (FALSE) or 1 (TRUE).
Step 2: List All Possible Combinations
We need to list all possible combinations of the values for X and Y. There are 2 variables, and each can take 2 values (0 or 1), resulting in 22=4 combinations:
- X=0,Y=0
- X=0,Y=1
- X=1,Y=0
- X=1,Y=1
Step 3: Calculate (X∧Y)
Next, we will calculate the result of the logical AND operation (X∧Y) for each combination:
- For (0∧0): Result is 0
- For (0∧1): Result is 0
- For (1∧0): Result is 0
- For (1∧1): Result is 1
Step 4: Calculate Z=(X∧Y)∨X
Now, we will calculate Z using the results from the AND operation and the value of X:
- For X=0,Y=0: Z=(0)∨0=0
- For X=0,Y=1: Z=(0)∨0=0
- For X=1,Y=0: Z=(0)∨1=1
- For X=1,Y=1: Z=(1)∨1=1
Step 5: Construct the Truth Table
Now we can compile the results into a truth table:
| X | Y | X∧Y | Z |
|---------|---------|------------------|---------|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Final Result
The truth table for the logical function Z=(X∧Y)∨X is complete.
---
The variables involved in the function are X and Y. Each variable can take a value of either 0 (FALSE) or 1 (TRUE).
We need to list all possible combinations of the values for X and Y. There are 2 variables, and each can take 2 values (0 or 1), resulting in 22=4 combinations:
- X=0,Y=1
- X=1,Y=0
- X=1,Y=1
Next, we will calculate the result of the logical AND operation (X∧Y) for each combination:
- For (0∧1): Result is 0
- For (1∧0): Result is 0
- For (1∧1): Result is 1
Now, we will calculate Z using the results from the AND operation and the value of X:
- For X=0,Y=1: Z=(0)∨0=0
- For X=1,Y=0: Z=(0)∨1=1
- For X=1,Y=1: Z=(1)∨1=1
Now we can compile the results into a truth table:
|---------|---------|------------------|---------|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
The truth table for the logical function Z=(X∧Y)∨X is complete.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - Worked out examples11videos
SEMICONDUCTOR AND SEMICONDUCTOR DEVICES
- BOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - objective I13videos
SEMICONDUCTOR AND SEMICONDUCTOR DEVICES
- BOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions38videos
PHOTOMETRY
- BOOK - HC VERMA ENGLISHCHAPTER - SPEED OF LIGHTEXERCISE - Question for short Answer5videos
SPEED OF LIGHT
Similar Questions
Knowledge Check
- Question 1 - Select One

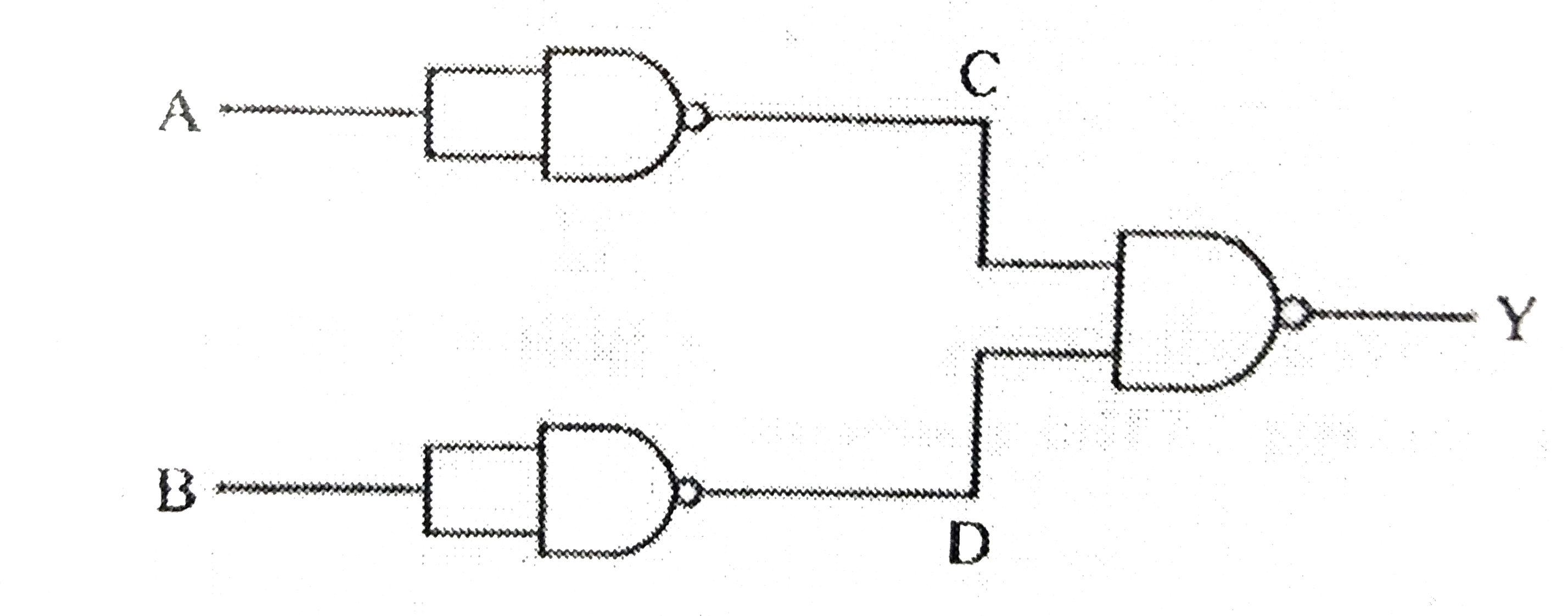
The truth table of the logic circuit shown-A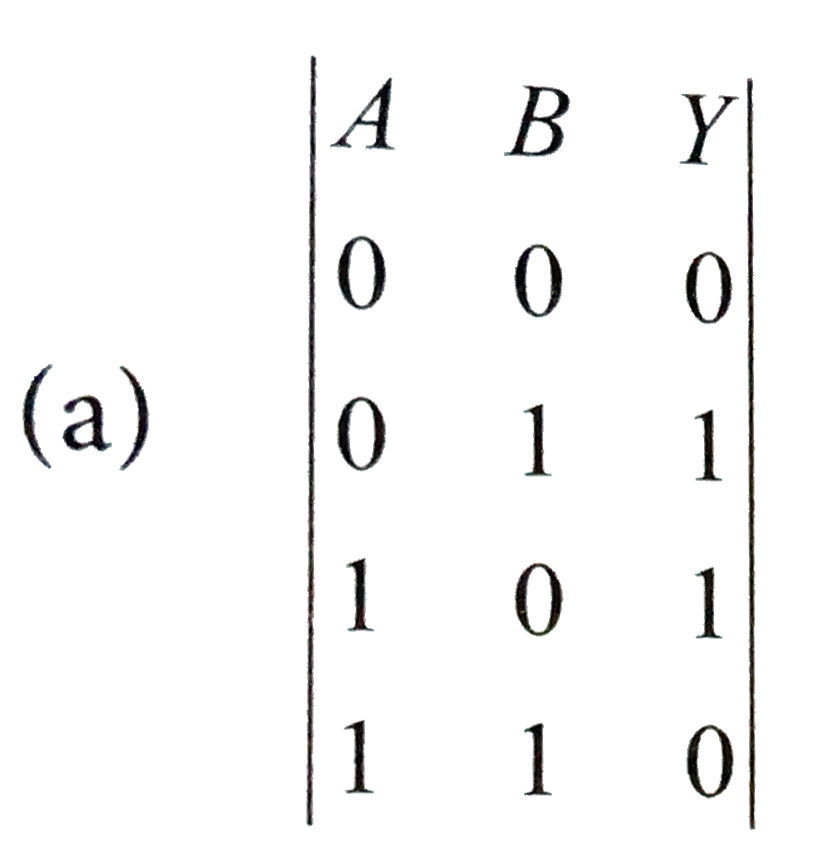 B
B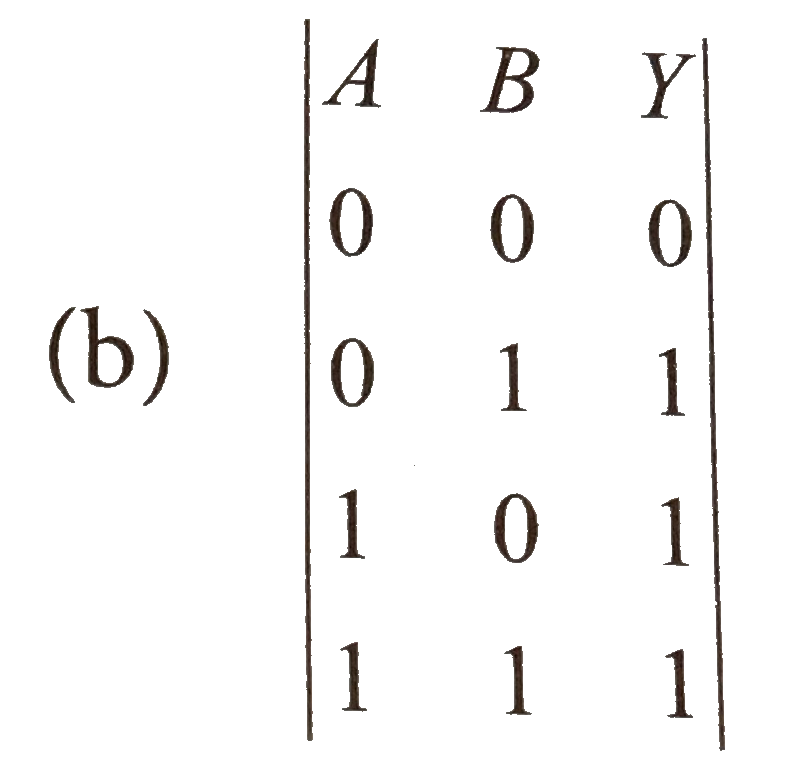 C
C D
D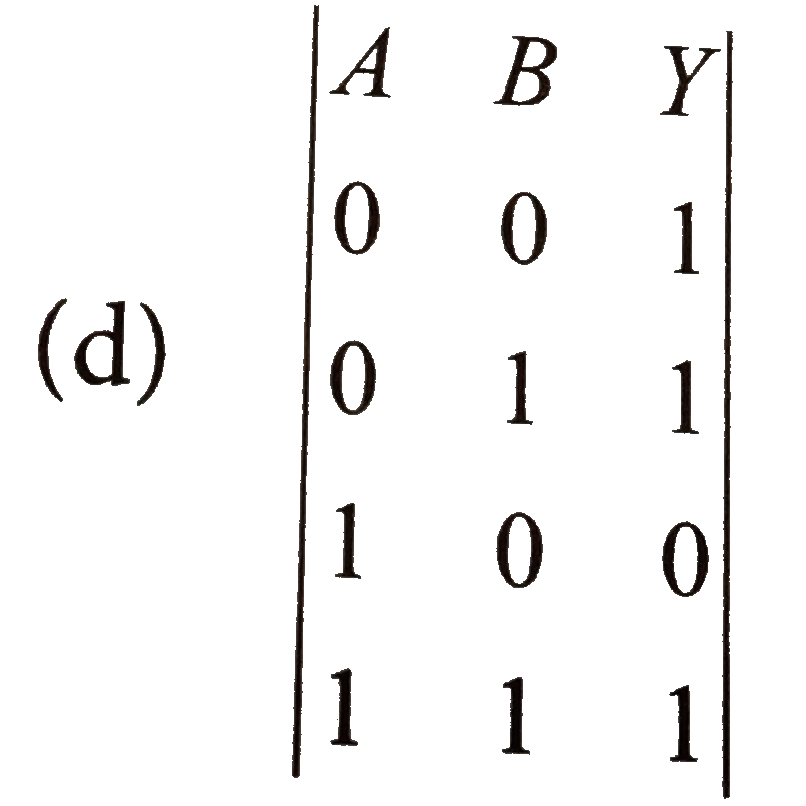
The Fig shown input waveforms A and B to a logic gate. Draw the output waveform for an OR gate. Write the truth table for this logic gate and draw its logic symbol.
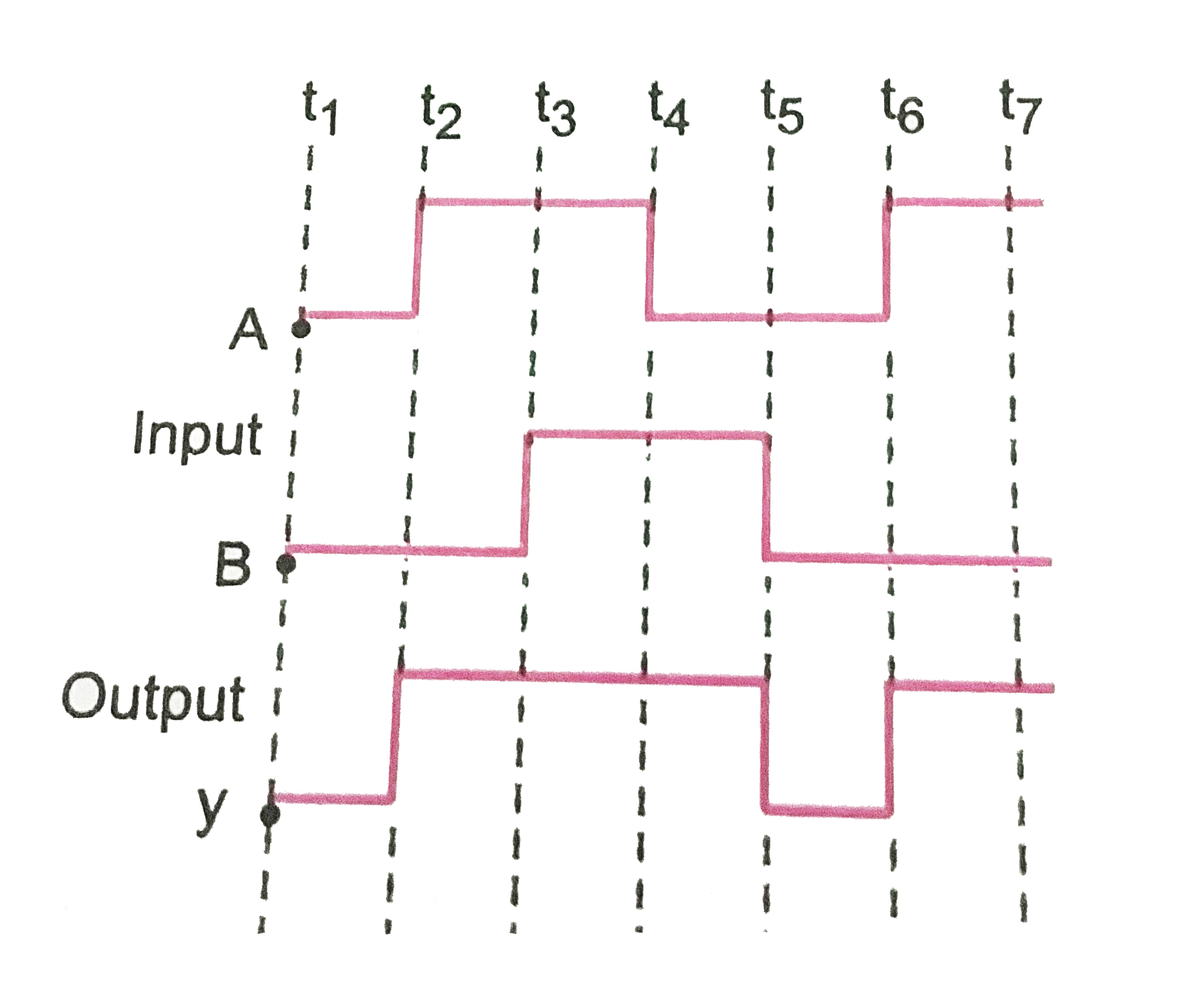 View Solution
View SolutionConstruct the truth table for the function X of A and B represented by figure.
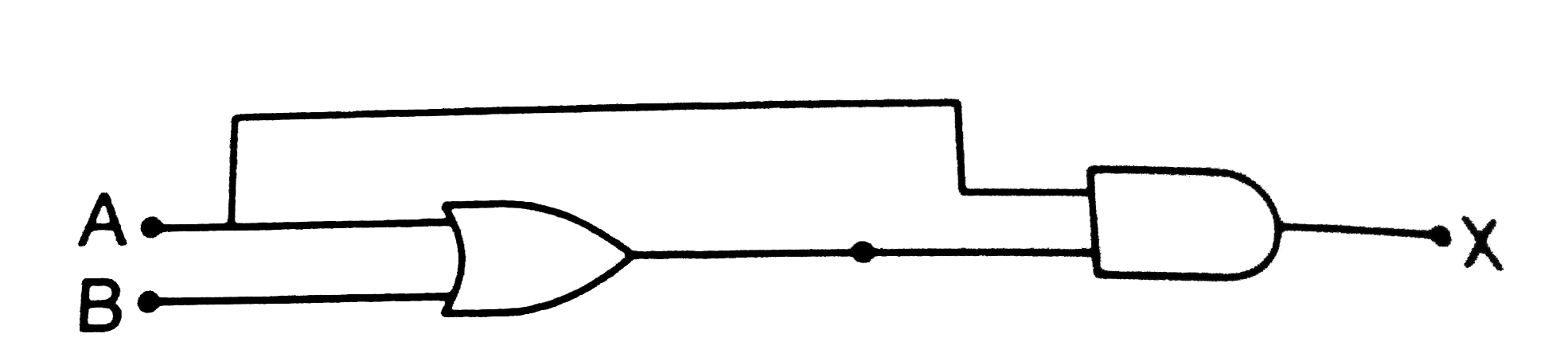 View Solution
View SolutionWrite the truth table for the combination of the gates shown in the figure.
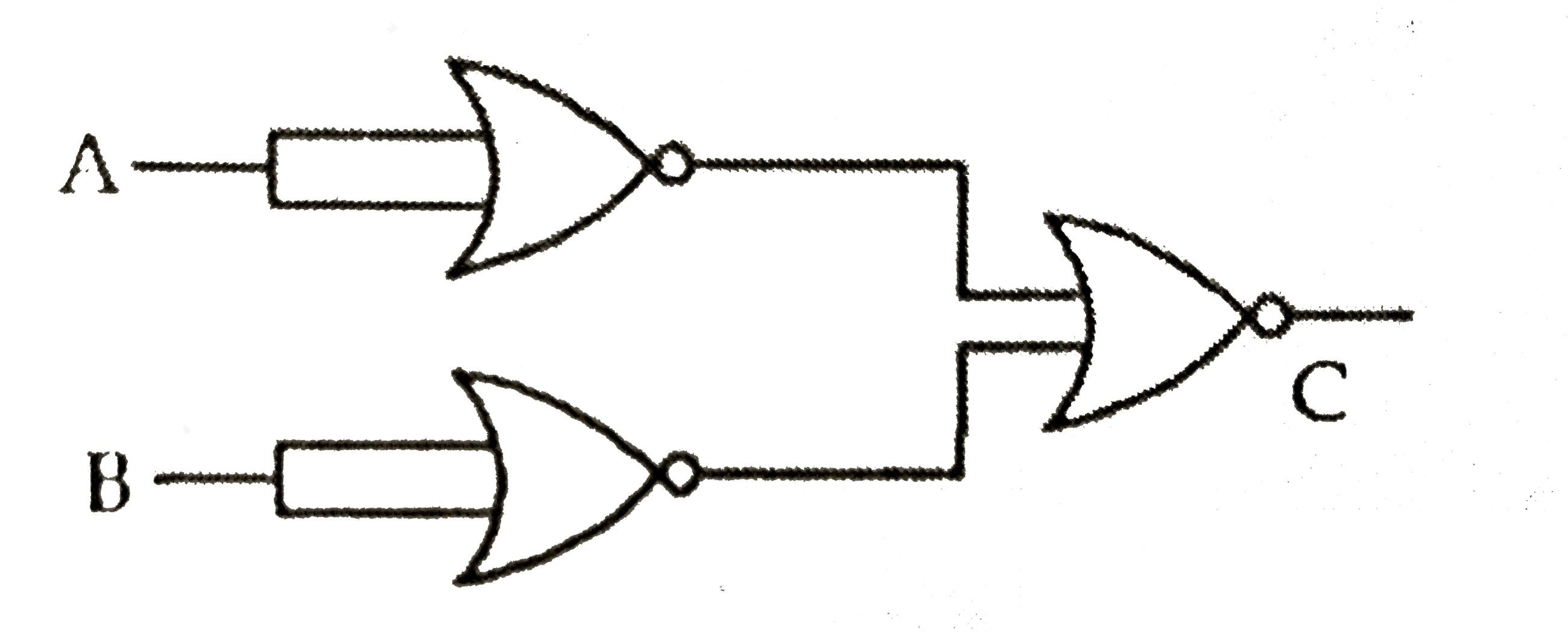 View Solution
View SolutionIdentify the gates P and Q shown in the figure. Write the truth table for the combination of the gates shown.

Name the equivalent gate representing this circuit and write its logic symbol.View SolutionWrite the truth table for the combination of the getes shown. Name the gates used.
View SolutionWrite the truth table for the circuit given in Fig., consisting of NOR gates only. Identify the logic operations (OR, AND, NOT) performed by two circuits.
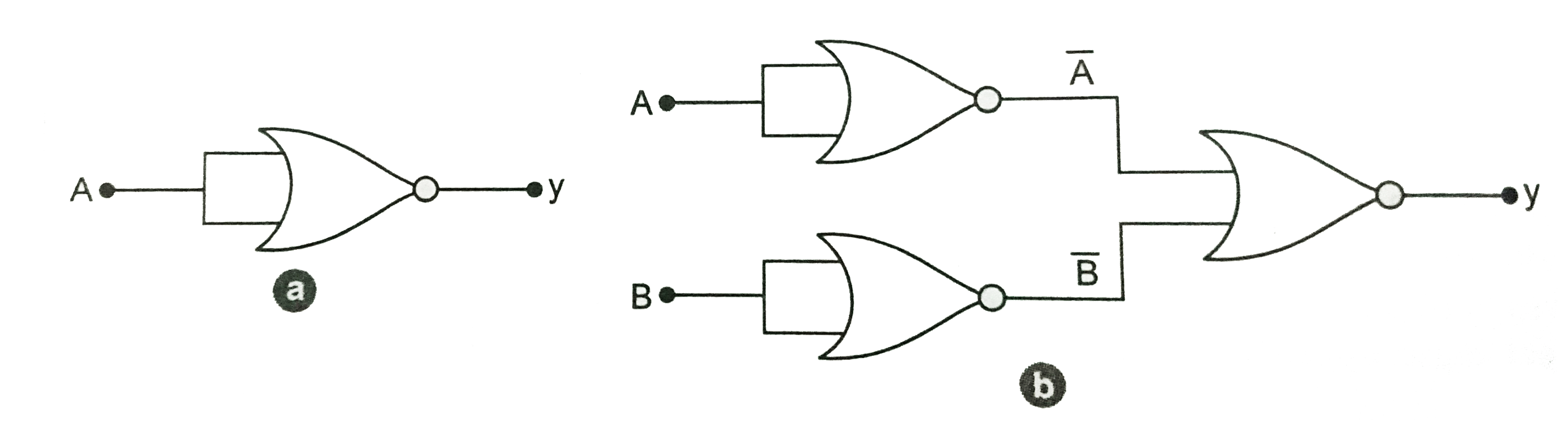 View Solution
View SolutionWrite the truth table for the circuit given in Fig., consisting of NOR gates only. Identify the logic operations (OR, AND, NOT) performed by two circuits.
 View Solution
View Solution