The band gap in germanium is (ΔE=0.68eV.).Assuming that the number of hole-electron pairs is proportional to e^(-Delta E//2kT),find the percentage increase in the number of charge carries in pure germanium as the temperature is increased form 300K to 320K.
To find the percentage increase in the number of charge carriers in pure germanium as the temperature increases from 300K to 320K, we can follow these steps:
Step 1: Understand the relationship between charge carriers and temperature
The number of hole-electron pairs (charge carriers) in germanium is given by the formula:
N∝e−ΔE2kT
where:
- ΔE is the band gap energy (0.68 eV for germanium),
- k is the Boltzmann constant (8.62×10−5 eV/K),
- T is the absolute temperature in Kelvin.
Step 2: Define the number of charge carriers at two temperatures
Let:
- N1 be the number of charge carriers at temperature T1=300K,
- N2 be the number of charge carriers at temperature T2=320K.
Using the relationship:
N1=N0e−ΔE2kT1
N2=N0e−ΔE2kT2
Step 3: Calculate the values of N1 and N2
Substituting the values into the equations:
- For N1:
N1=N0e−0.682×8.62×10−5×300
- For N2:
N2=N0e−0.682×8.62×10−5×320
Step 4: Simplify the expressions for N1 and N2
Calculating the exponent for N1:
0.682×8.62×10−5×300≈13.2
Thus,
N1=N0e−13.2
Calculating the exponent for N2:
0.682×8.62×10−5×320≈12.6
Thus,
N2=N0e−12.6
Step 5: Calculate the percentage increase in charge carriers
The percentage increase in the number of charge carriers is given by:
Percentage Increase=N2−N1N1×100
Substituting the expressions for N1 and N2:
Percentage Increase=N0e−12.6−N0e−13.2N0e−13.2×100
This simplifies to:
Percentage Increase=(e−12.6−e−13.2)×100e−13.2
Step 6: Calculate the final result
Calculating the values:
- e−12.6≈3.2×10−6
- e−13.2≈1.8×10−6
Thus:
Percentage Increase=(3.2×10−6−1.8×10−6)×1001.8×10−6
Percentage Increase=(1.4×10−6)×1001.8×10−6≈77.78%
Final Answer
The percentage increase in the number of charge carriers in pure germanium as the temperature is increased from 300K to 320K is approximately 77.78%.
---
The number of hole-electron pairs (charge carriers) in germanium is given by the formula:
N∝e−ΔE2kT
where:
- ΔE is the band gap energy (0.68 eV for germanium),
- k is the Boltzmann constant (8.62×10−5 eV/K),
- T is the absolute temperature in Kelvin.
Let:
- N1 be the number of charge carriers at temperature T1=300K,
- N2 be the number of charge carriers at temperature T2=320K.
N1=N0e−ΔE2kT1
N2=N0e−ΔE2kT2
Substituting the values into the equations:
- For N1:
N1=N0e−0.682×8.62×10−5×300
- For N2:
N2=N0e−0.682×8.62×10−5×320
Calculating the exponent for N1:
0.682×8.62×10−5×300≈13.2
Thus,
N1=N0e−13.2
0.682×8.62×10−5×320≈12.6
Thus,
N2=N0e−12.6
The percentage increase in the number of charge carriers is given by:
Percentage Increase=N2−N1N1×100
Percentage Increase=N0e−12.6−N0e−13.2N0e−13.2×100
Percentage Increase=(e−12.6−e−13.2)×100e−13.2
Calculating the values:
- e−12.6≈3.2×10−6
- e−13.2≈1.8×10−6
Percentage Increase=(3.2×10−6−1.8×10−6)×1001.8×10−6
Percentage Increase=(1.4×10−6)×1001.8×10−6≈77.78%
The percentage increase in the number of charge carriers in pure germanium as the temperature is increased from 300K to 320K is approximately 77.78%.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - objective I13videos
SEMICONDUCTOR AND SEMICONDUCTOR DEVICES
- BOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - objective II8videos
SEMICONDUCTOR AND SEMICONDUCTOR DEVICES
- BOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - Question for short answer11videos
SEMICONDUCTOR AND SEMICONDUCTOR DEVICES
- BOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions38videos
PHOTOMETRY
- BOOK - HC VERMA ENGLISHCHAPTER - SPEED OF LIGHTEXERCISE - Question for short Answer5videos
SPEED OF LIGHT
Similar Questions
The conductivity of a pure semiconductor is roughly proportional to T32e−ΔE/2kT where (Δ)E is the band gap. The band gap for germanium is 0.74eV at 4K and 0.67eV at 300K.By what factor does the conductivity of pure germanium increase as the temperature is raised form 4K to 300K?
View SolutionLet (Δ)Edenote the energy gap between the valence band and the conduction band.The population of conduction electrons (and of the holes)is roughly proportional to e−ΔE/2kT.Find the ratio of the concentration of conduction electrons in diamond to that in silicon at room tempareture 300K.(ΔE)for silicon is 1.1 ev and for diamond is 6.0eV.How many conduction electrons are likely to be in one cubic meter of diamond ?
View SolutionTwo reaction : X→ Products and Y→ Products have rate constants k1 and k2 at temperature T and activation energies E1 and E2, respectively. If k1>k2 and E1<E2 (assuming that the Arrhenius factor is same for both the Products), then
(I) On increaisng the temperature, increase in k2 will be greater than increaisng in k1.
(II) On increaisng the temperature, increase in k1 will be greater than increase in k2.
(III) At higher temperature, k1 will be closer to k2.
(IV) At lower temperature, k1<k2View SolutionWhen a semiconducting meterial is doped with an impurity,new acceptor levels are created .In a particular thermal collision,a valence electrons recives an energy equal to 2kT and just reaches one of the acceptor levels. Assuming that the energy of the electron was at the top edge of hte valence band and that the temperature T is equal to 300K, find the energy of the acceptor levels above the valence band.
View SolutionThe rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given the number triples in 5 hrs., find how many bacteria will be present after 10 hours. Also find the time necessary for the number of bacteria to be 10 times the number of initial present. [Given loge3=1.0986, e2.1972=9 ]
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
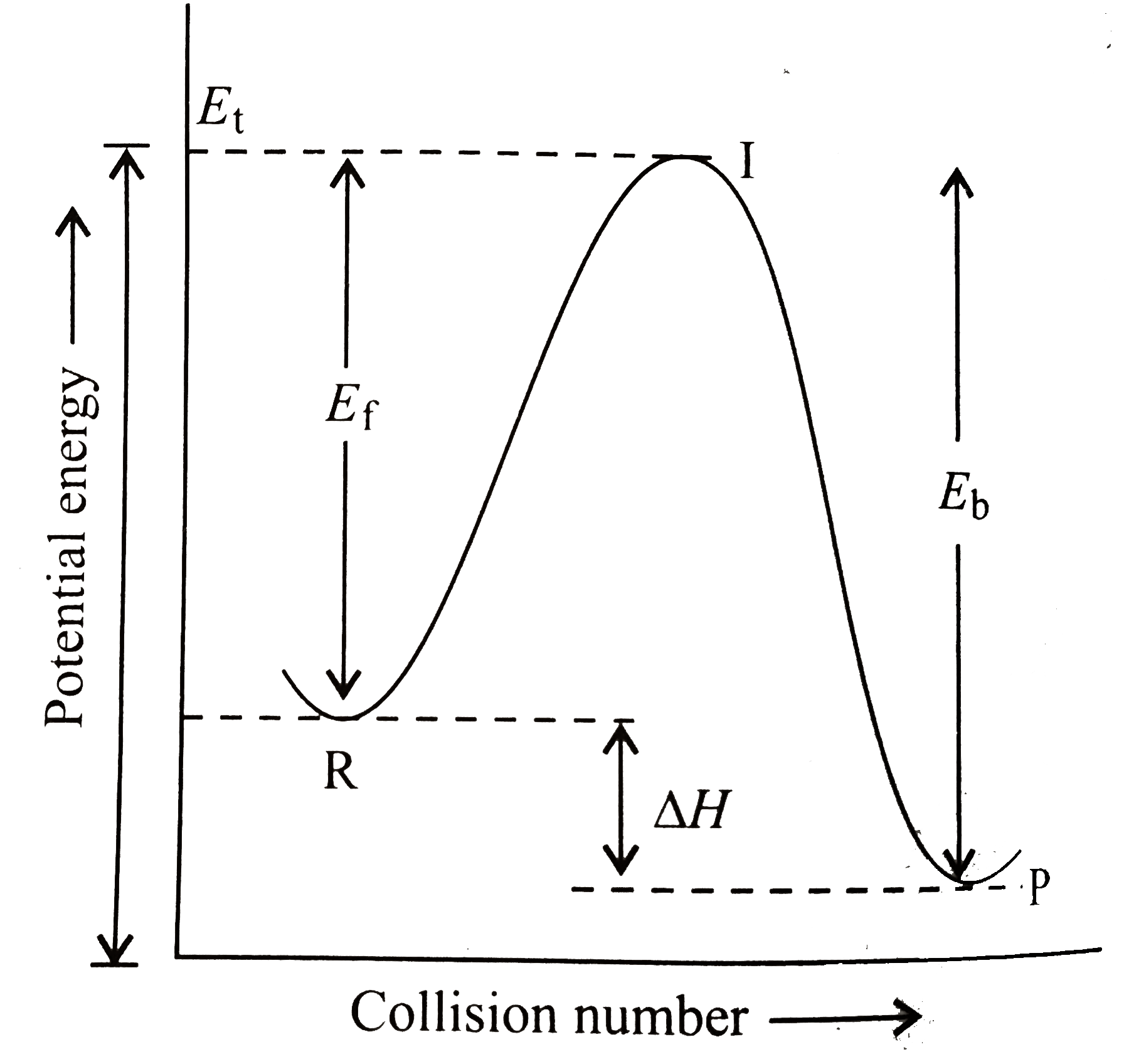
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The rate constant of a certain reaction is given by k=Ae−Ea/RT
(where A= Arrhenius constant). Which factor should be lowered so that the rate of reaction may increase?View SolutionAn ideal gas (γ=3/2) is compressed adiabatically form volume 400cm3 to 100cm3. The initial pressure and temperature are 100kPa and 400K. Find (a) the number of moles of the gas (b) the molar heat capacity at constant pressure, (c ) the final pressure and temperature, (d) the work done by the gas in the process and (e) the change in internal energy of the gas.(R=253J/mol−k)
View SolutionThermal decomposition of gaseous X2 to gaseous X at 298K takes place according to the following equation:
X(g)⇔2X(g)
The standard reaction Gibbs energy ΔrG∘, of this reaction is positive. At the start of the reaction, there is one mole of X2 and no X. As the reaction proceeds, the number of moles of X formed is given by β. Thus βequilibrium is the number of moles of X formed at equilibrium. The reaction is carried out at a constant total pressure of 2 bar. Consider the gases to behave ideally.
[Given, R=0.083L bar K−1mol−1)
The equilibrium constant Kp for this reaction at 298K, in terms of βequilibrium isView SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A uniform wire of length 2.0 m and cross-sectional area 10−7m2 carries a current of 1.6 A. If there are 1028 free electrons per m in copper, the drift speed of electrons in copper is
View SolutionWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
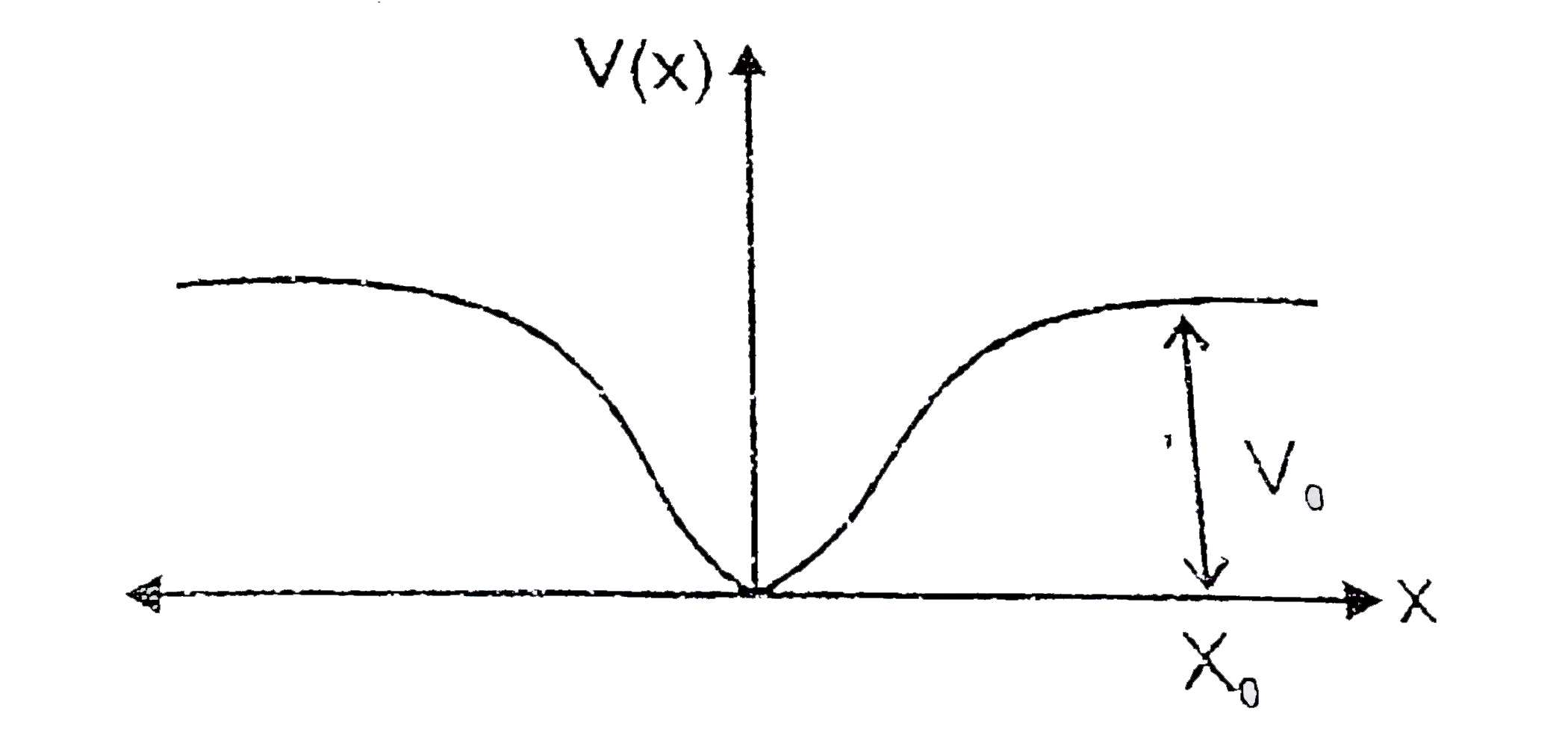
If the total energy of the particle is E, it will perform is periodic motion why if :View Solution

