Suppose two elements X and Y combine to form two compound XY2andX2Y3weighs 85g. The atomic masses of X and Y are respectively :
To solve the problem, we need to find the atomic masses of elements X and Y based on the information given about the two compounds they form, XY2 and X2Y3, both weighing 85g.
Step 1: Set up the equations based on the compounds
1. For the compound XY2:
- The molar mass of XY2 is given by the formula:
MXY2=X+2Y
- Since the total mass is 85g, we can write the equation:
X+2Y=85(Equation 1)
2. For the compound X2Y3:
- The molar mass of X2Y3 is given by the formula:
MX2Y3=2X+3Y
- Again, since the total mass is 85g, we can write the equation:
2X+3Y=85(Equation 2)
Step 2: Manipulate the equations
1. Multiply Equation 1 by 2:
2(X+2Y)=2×85⟹2X+4Y=170(Equation 3)
Step 3: Subtract Equation 2 from Equation 3
1. Now, subtract Equation 2 from Equation 3:
(2X+4Y)−(2X+3Y)=170−85
This simplifies to:
4Y−3Y=85⟹Y=85
Step 4: Substitute the value of Y back into Equation 1
1. Substitute Y=85 into Equation 1:
X+2(85)=85
This simplifies to:
X+170=85
Rearranging gives:
X=85−170⟹X=−85
Conclusion
The atomic masses calculated are:
- X=−85
- Y=85
Since atomic masses cannot be negative, this indicates that there is an inconsistency in the data provided. Therefore, we need to re-evaluate the problem or check for errors in the given data.
1. For the compound XY2:
- The molar mass of XY2 is given by the formula:
MXY2=X+2Y
- Since the total mass is 85g, we can write the equation:
X+2Y=85(Equation 1)
- The molar mass of X2Y3 is given by the formula:
MX2Y3=2X+3Y
- Again, since the total mass is 85g, we can write the equation:
2X+3Y=85(Equation 2)
1. Multiply Equation 1 by 2:
2(X+2Y)=2×85⟹2X+4Y=170(Equation 3)
1. Now, subtract Equation 2 from Equation 3:
(2X+4Y)−(2X+3Y)=170−85
This simplifies to:
4Y−3Y=85⟹Y=85
1. Substitute Y=85 into Equation 1:
X+2(85)=85
This simplifies to:
X+170=85
Rearranging gives:
X=85−170⟹X=−85
The atomic masses calculated are:
- X=−85
- Y=85
Similar Questions
Suppose two elements X and Y combine to form two compounds XY2 and X2Y3 when 0.05 mole of XY2 weight 5g while 3.011×1023 molecules of X2Y3 weight 85g. The atomic masses of X and Y are respectively.
View SolutionSuppose elements X and Y combine to form two compounds XY2 and X3Y2 when 0.1 mole of former weigh 10g while 0.05 mole of the latter weigh 9g. What are the atomc weights of X and Y.
View Solution
Knowledge Check
- Question 1 - Select One
Two elements X and Y combine to form a compound XY. Under what conditions the bond formed between them will be ionic ?
AIf the difference in electronegativities of X and Y is 1.7.BIf the difference in electronegativities of X and Y is more than 1.7.CIf the difference in electronegativities of X and Y is less than 1.7.DIf both X and Y are highly electronegative. - Question 2 - Select One
Two alkenes, X(91% yield) and Y(9% yield) are formed when the following compound is heated.
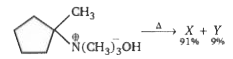
The structures of X and Y, respectively are :A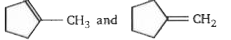 B
B C
C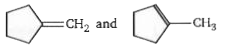 D
D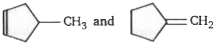
- Question 3 - Select One
If the two lines of regression are 2x−y−4=0 and 9x−2y−38=0, then the means of x and y variates respectively are
A8, 6B6, 8C7 , 10D5, 6
Two elements X (at.mass 16) and Y (at.mass 14) combine to form compounds A,BandC. The ratio be different masses of Y which combine with a fixed mass of X in A,BandC is 1:3:5. If 32 parts by mass of X combines with 84 parts by mass of Y in B then in C,16 parts by mass of X will combine with ...... parts by mass of Y :
View SolutionTwo elements P and Q combine to form two different compounds in stoichimetric ratios of 1:2 and 1:3.If 0.25 mole of 1st compound weighs 16 g and 0.05 mole of 2nd compound weighs 4 g, then the atomic weighs of P and Q respectively are
View SolutionA compound contains elements X and Y in 1 : 4 mass ratio. If the atomic masses of X and Y are in ratio 1 : 2, then empirical formula will be
View SolutionThe elements X and Y form compound having molecular formula XY2 and XY4 (both are non - electrolysis), when dissolved in 20 g benzene, 1 g XY2 lowers the freezing point by 2.3∘C whereas 1 g of XY4 lowers the freezing point by 1.3∘(C). Molal depression constant for benzene is 5.1. Thus atomic masses of X and Y respectively are
View SolutionX and Y are two elements which form X2Y3 and X3Y4. If 0.20 mol of X2Y3 weight 32.0g and 0.4mol of X3Y4 weigths 92.8g, the atomic weights of X and Y are respectively
View Solution

