For a reaction initial rate is given as : R0=k[A0]2[B0]. By what factor, the initial rate of reaction will increase if initial concentration is taken 1.5 times and B is tripled?
4.5
2.25
6.75
None of these
The correct Answer is:C
To solve the problem, we need to analyze how the initial rate of reaction changes when the concentrations of reactants are altered. The initial rate of the reaction is given by the equation:
R0=k(A0)2(B0)
Where:
- R0 is the initial rate of reaction.
- k is the rate constant.
- (A0) is the initial concentration of reactant A.
- (B0) is the initial concentration of reactant B.
Step 1: Define the new concentrations
According to the problem:
- The initial concentration of A is increased to 1.5 times, so:
(A)=1.5(A0)=32(A0)
- The initial concentration of B is tripled, so:
(B)=3(B0)
Step 2: Substitute the new concentrations into the rate equation
Now, we can substitute these new concentrations into the rate equation:
R′=k(32(A0))2(3(B0))
Step 3: Simplify the equation
Calculating (32(A0))2:
(32(A0))2=94(A0)2
Now substituting this back into the rate equation:
R′=k(94(A0)2)(3(B0))
Step 4: Combine the terms
Now we can combine the terms:
R′=k⋅94⋅3⋅(A0)2⋅(B0)
R′=k⋅274(A0)2(B0)
Step 5: Relate the new rate to the original rate
Now we can relate R′ to R0:
R′=274R0
Step 6: Calculate the factor of increase
To find the factor by which the initial rate of reaction increases, we can write:
Factor of increase=R′R0=274
Final Answer
Thus, the initial rate of reaction will increase by a factor of 274 or 6.75.
---
- R0 is the initial rate of reaction.
- k is the rate constant.
- (A0) is the initial concentration of reactant A.
- (B0) is the initial concentration of reactant B.
According to the problem:
- The initial concentration of A is increased to 1.5 times, so:
(A)=1.5(A0)=32(A0)
- The initial concentration of B is tripled, so:
(B)=3(B0)
Now, we can substitute these new concentrations into the rate equation:
Calculating (32(A0))2:
(32(A0))2=94(A0)2
R′=k(94(A0)2)(3(B0))
Now we can combine the terms:
R′=k⋅94⋅3⋅(A0)2⋅(B0)
R′=k⋅274(A0)2(B0)
Now we can relate R′ to R0:
R′=274R0
To find the factor by which the initial rate of reaction increases, we can write:
Factor of increase=R′R0=274
Thus, the initial rate of reaction will increase by a factor of 274 or 6.75.
Similar Questions
For a zero order reaction '[R]0 is the initial concentration
View SolutionFor a hypothetical reaction A→B, it is found that the rate constant =xs−1. By what factor the rate is increased if the initial concentration of A is tripled?
View SolutionFor zero order reaction , t1/2 will be (A0 is the initial concentration , K is rate constant)
View SolutionFor a first order reaction with rate constant 'k' and initial concentration 'a', the half-life period is given by
View SolutionFor a first order reaction with rate constant 'k' and initial concentration 'a', the half-life period is given by
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentrations of A and B as given below:
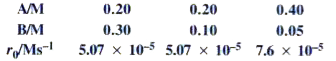
What is the order of reaction with respect to A and B ?
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentrations of A and B as given below:
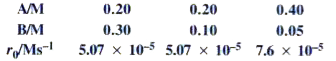
What is the order of reaction with respect to A and B ?
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentrations of A and B as given below:
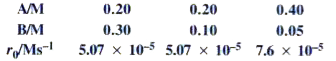
What is the order of reaction with respect to A and B ?
View SolutionIn a reaction A + B → Products
(i) If the initial concentration of A is doubled and B is kept constant, the rate of the reaction is doubled
(ii) If the initial concentration both A and B are doubled the rate of reaction becomes eight times
The rate law of the reaction is :
View SolutionFor the chemical reaction A+2B→C, the rate of reaction is increased by 2.82 times when the concentration of A is doubled and increased by 9 times when the concentration of B was tripled. What is the order with respect to B and A and total order ?
View Solution
