In a hexagonal crystal:
The correct Answer is:D
To determine the cell parameters of a hexagonal crystal system, we need to understand the relationships between the edge lengths and the angles. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Edge Lengths
In a hexagonal crystal system, the edge lengths are defined as:
- a = length of one edge
- b = length of the adjacent edge
- c = length of the vertical edge
For a hexagonal crystal:
- a=b (the two horizontal edges are equal)
- c is different from a and b (the vertical edge is not equal to the horizontal edges).
Step 2: Identify the Angles
The angles in a hexagonal crystal system are defined as:
- α = angle between edge b and edge c
- β = angle between edge a and edge c
- γ = angle between edge a and edge b
For a hexagonal crystal:
- α=90∘ (the angle between edge a and edge c)
- β=90∘ (the angle between edge b and edge c)
- γ=120∘ (the angle between the two equal edges a and b).
Step 3: Summarize the Parameters
From the above analysis, we can summarize the cell parameters for a hexagonal crystal system as follows:
- Edge lengths: a=b and c≠a
- Angles: α=90∘, β=90∘, γ=120∘
Step 4: Evaluate the Options
Now we can evaluate the given options based on the parameters we derived:
1. Option 1: α=β=γ≠90∘ - Incorrect
2. Option 2: All angles are equal - Incorrect
3. Option 3: All angles are equal to 90∘ - Incorrect
4. Option 4: a=b≠c, α=β=90∘, γ=120∘ - Correct
Conclusion
The correct option that describes the cell parameters of a hexagonal crystal system is the fourth option.
---
In a hexagonal crystal system, the edge lengths are defined as:
- a = length of one edge
- b = length of the adjacent edge
- c = length of the vertical edge
- a=b (the two horizontal edges are equal)
- c is different from a and b (the vertical edge is not equal to the horizontal edges).
The angles in a hexagonal crystal system are defined as:
- α = angle between edge b and edge c
- β = angle between edge a and edge c
- γ = angle between edge a and edge b
- α=90∘ (the angle between edge a and edge c)
- β=90∘ (the angle between edge b and edge c)
- γ=120∘ (the angle between the two equal edges a and b).
From the above analysis, we can summarize the cell parameters for a hexagonal crystal system as follows:
- Edge lengths: a=b and c≠a
- Angles: α=90∘, β=90∘, γ=120∘
Now we can evaluate the given options based on the parameters we derived:
1. Option 1: α=β=γ≠90∘ - Incorrect
2. Option 2: All angles are equal - Incorrect
3. Option 3: All angles are equal to 90∘ - Incorrect
4. Option 4: a=b≠c, α=β=90∘, γ=120∘ - Correct
The correct option that describes the cell parameters of a hexagonal crystal system is the fourth option.
Topper's Solved these Questions
- SOLID STATEBook:NARENDRA AWASTHI ENGLISHChapter:SOLID STATEExercise:Level-2
Explore 32 Videos
- SOLID STATEBook:NARENDRA AWASTHI ENGLISHChapter:SOLID STATEExercise:Level 3 passage -1
Explore 1 Video
- IONIC EEQUILIBRIUMBook:NARENDRA AWASTHI ENGLISHChapter:IONIC EEQUILIBRIUMExercise:Subjective problems
Explore 1 Video
- STOICHIOMETRYBook:NARENDRA AWASTHI ENGLISHChapter:STOICHIOMETRYExercise:Match the Colum-II
Explore 6 Videos
Similar Questions
In a tetragonal crystal
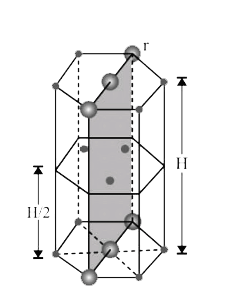
View SolutionIn a hexagonal system system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-packed is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed overt the first layer so that they touch each other and represent the second layer so that they touch each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is converted with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
(a)4
(b)6
(c)12
(d)17
View SolutionFerric oxide crystallizes in a hexagonal close packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of the ferric oxide.
View SolutionIn hexagonal system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space -filling model of this structure, called hexagonal close-packed (HCP), is consituted of a sphere on a flat surface surrouneded in the same plane by six identical spheres as closely possible. Three sphere are then palces over the first layer so that they touch each other and represent second layer is covered with third layer that is identical to the bottom layer in relative position. Assume radius of enery sphere to be r.

The number of atoms in the HPC unit cell is :
View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The volume of this HCP unit cell is

View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The empty space in this HCP unit cell is :
View SolutionIn hexagonal close packing of spherer in three dimensions.
View SolutionA: An ideal crystal has more entropy than a real crystal.
R: An ideal crystals has more disorder.
View SolutionIn a matallic crystal the .
View Solution......................is soft and slippery with a basic pattern of hexagonal rings.
View Solution