In an idaeal closet rock salt structure (edge length a) which of the following expression is correct?
ra=√2a
ra=a/√2
ra=a/2√2
ra=a/4
The correct Answer is:C
To solve the problem regarding the ideal rock salt structure (NaCl) and its edge length a, we can follow these steps:
1. Understanding the Structure:
The rock salt structure is a face-centered cubic (FCC) lattice where chloride ions (Cl−) occupy the face-centered positions and sodium ions (Na+) occupy the octahedral voids.
2. Identifying the Unit Cell:
In the FCC structure, the unit cell has atoms at the corners and at the centers of each face. The edge length of the unit cell is given as a.
3. Finding the Face Diagonal:
In an FCC lattice, the face diagonal can be calculated using the Pythagorean theorem. For a face of the cube, the face diagonal d can be expressed as:
d=√a2+a2=√2a2=a√2
4. Relating the Face Diagonal to Atomic Radii:
In the rock salt structure, the face diagonal is equal to the sum of the diameters of the two corner atoms and the face-centered atom. Since the radius of each ion is r, the face diagonal can be expressed as:
d=4r
Thus, we have:
a√2=4r
5. Solving for the Radius r:
Rearranging the equation gives:
r=a√24
This can be simplified further:
r=a2√2
6. Conclusion:
The expression for the radius r of the ions in the ideal rock salt structure is:
r=a2√2
Therefore, the correct option that represents this expression is a2√2.
The rock salt structure is a face-centered cubic (FCC) lattice where chloride ions (Cl−) occupy the face-centered positions and sodium ions (Na+) occupy the octahedral voids.
In the FCC structure, the unit cell has atoms at the corners and at the centers of each face. The edge length of the unit cell is given as a.
In an FCC lattice, the face diagonal can be calculated using the Pythagorean theorem. For a face of the cube, the face diagonal d can be expressed as:
d=√a2+a2=√2a2=a√2
In the rock salt structure, the face diagonal is equal to the sum of the diameters of the two corner atoms and the face-centered atom. Since the radius of each ion is r, the face diagonal can be expressed as:
d=4r
Thus, we have:
a√2=4r
Rearranging the equation gives:
r=a√24
This can be simplified further:
r=a2√2
The expression for the radius r of the ions in the ideal rock salt structure is:
r=a2√2
Therefore, the correct option that represents this expression is a2√2.
Topper's Solved these Questions
- SOLID STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - SOLID STATEEXERCISE - Level-2
32 Videos
- SOLID STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - SOLID STATEEXERCISE - Level 3 passage -1
1 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems
1 Videos
- STOICHIOMETRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Match the Colum-II
6 Videos
Similar Questions
Knowledge Check
Which of the following expressions regarding entropy is not correct?
AΔSsystem=qTBΔSsystem=ΔStotal+ΔSsurroundingCΔS=ΔSfinal−SinitialDΔStotal=ΔSsystem+ΔSsurrounding
Which one of the following is correct structure of 'B'?A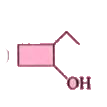 B
B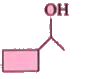 C
C D
D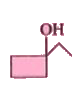
Which of the following expression is/are correct ?
View SolutionCsCl crystallizes in body centred cubic lattice .If 'a' is its edge length then which of the following expression is correct?
View SolutionCsCl crystallises in body centred cubic lattice. If 'a' is its edge length then which of the following expression is correct ?
View SolutionWhich of the following is correct for zeise.s salt ?
View SolutionWhich of the following contains rock salt structure?
View SolutionWhich of the following practical units of length is not correct?
View Solution
