Which of the following is the most correct expression for Heisenberg's uncerainty principle?
△x.△p=h4π
△x.△p≥h4π
△x.△p≤h4π
△x.△v=h4π
The correct Answer is:B
To solve the question regarding Heisenberg's uncertainty principle, we will follow these steps:
Step 1: Understand Heisenberg's Uncertainty Principle
Heisenberg's uncertainty principle states that it is impossible to simultaneously know both the position and momentum of a particle with absolute precision. The more accurately we know one of these quantities, the less accurately we can know the other.
Step 2: Identify the Mathematical Expression
The principle can be mathematically expressed as:
Δx⋅Δp≥h4π
where:
- Δx is the uncertainty in position,
- Δp is the uncertainty in momentum,
- h is Planck's constant.
Step 3: Relate Momentum to Velocity
Momentum p is defined as:
p=mv
where m is the mass and v is the velocity of the particle. Therefore, the uncertainty in momentum can be expressed as:
Δp=m⋅Δv
where Δv is the uncertainty in velocity.
Step 4: Substitute into the Uncertainty Principle
Substituting Δp into the uncertainty principle gives us:
Δx⋅m⋅Δv≥h4π
Step 5: Analyze the Given Options
Now, we need to analyze the provided options to determine which one correctly represents the Heisenberg uncertainty principle:
1. If an option shows only an equality (e.g., Δx⋅Δp=h4π), it is incorrect because the principle states an inequality.
2. If an option states Δx⋅Δp<h4π, it is also incorrect for the same reason.
3. If an option omits mass when discussing momentum, it is incorrect.
Conclusion
After analyzing the options based on the steps above, the correct expression for Heisenberg's uncertainty principle is:
Δx⋅Δp≥h4π
Thus, the correct answer is option B.
---
Heisenberg's uncertainty principle states that it is impossible to simultaneously know both the position and momentum of a particle with absolute precision. The more accurately we know one of these quantities, the less accurately we can know the other.
The principle can be mathematically expressed as:
Δx⋅Δp≥h4π
where:
- Δx is the uncertainty in position,
- Δp is the uncertainty in momentum,
- h is Planck's constant.
Momentum p is defined as:
p=mv
where m is the mass and v is the velocity of the particle. Therefore, the uncertainty in momentum can be expressed as:
Δp=m⋅Δv
where Δv is the uncertainty in velocity.
Substituting Δp into the uncertainty principle gives us:
Δx⋅m⋅Δv≥h4π
Now, we need to analyze the provided options to determine which one correctly represents the Heisenberg uncertainty principle:
1. If an option shows only an equality (e.g., Δx⋅Δp=h4π), it is incorrect because the principle states an inequality.
2. If an option states Δx⋅Δp<h4π, it is also incorrect for the same reason.
3. If an option omits mass when discussing momentum, it is incorrect.
After analyzing the options based on the steps above, the correct expression for Heisenberg's uncertainty principle is:
Δx⋅Δp≥h4π
Thus, the correct answer is option B.
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
Knowledge Check
Which of the following is most polar?
A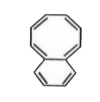 B
B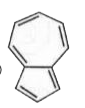 C
C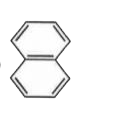 D
D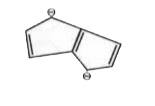
Which of the following is most basic?
A B
B C
C D
D
Explain Heisenberg's uncertainty principle .
View SolutionWhich of the following is most basic ?
View SolutionWhich of the following is most reactive ?
View SolutionWhich of the following is most acidic ?
View SolutionWhich of the following is most soluble?
View SolutionWhich of the following is most acidic ?
View Solution
