In Schrodinger wave mechanical model represents :
amplitude of electron wave
probability density of electron
total probaility of finding electron around nucleus
orbit
The correct Answer is:B
To solve the question regarding the representation of Ψ2(r,θ,ϕ) in the context of the Schrödinger wave mechanical model, we can follow these steps:
1. Understanding the Wave Function (Ψ):
- The wave function, denoted as Ψ(r, θ, φ), is a mathematical function that describes the quantum state of a particle, in this case, an electron in an atom. It is a solution to the Schrödinger equation.
Hint: Recall that the wave function contains information about the quantum state of a system.
2. Components of the Wave Function:
- The wave function can be separated into two parts: a radial part and an angular part. The radial part depends on the distance from the nucleus (r), while the angular part depends on the angles θ (theta) and φ (phi).
Hint: Think about how the wave function can be expressed in spherical coordinates.
3. Interpreting Ψ²:
- The term Ψ²(r, θ, φ) represents the square of the wave function. In quantum mechanics, the square of the wave function gives us the probability density of finding the electron in a particular region of space.
Hint: Remember that in quantum mechanics, probabilities are derived from the square of the wave function.
4. Probability Density:
- Specifically, Ψ²(r, θ, φ) provides the probability density function for the electron's position. This means it tells us how likely it is to find the electron at a certain point in space, defined by the coordinates (r, θ, φ).
Hint: Consider how probability density relates to the likelihood of finding a particle in a specific area.
5. Conclusion:
- Therefore, in the context of the Schrödinger wave mechanical model, Ψ²(r, θ, φ) represents the probability density of the electron.
Hint: Think about the implications of probability density in the context of electron distribution around the nucleus.
Final Answer:
In the Schrödinger wave mechanical model, Ψ²(r,θ,φ) represents the probability density of the electron.
- The wave function, denoted as Ψ(r, θ, φ), is a mathematical function that describes the quantum state of a particle, in this case, an electron in an atom. It is a solution to the Schrödinger equation.
- The wave function can be separated into two parts: a radial part and an angular part. The radial part depends on the distance from the nucleus (r), while the angular part depends on the angles θ (theta) and φ (phi).
- The term Ψ²(r, θ, φ) represents the square of the wave function. In quantum mechanics, the square of the wave function gives us the probability density of finding the electron in a particular region of space.
- Specifically, Ψ²(r, θ, φ) provides the probability density function for the electron's position. This means it tells us how likely it is to find the electron at a certain point in space, defined by the coordinates (r, θ, φ).
- Therefore, in the context of the Schrödinger wave mechanical model, Ψ²(r, θ, φ) represents the probability density of the electron.
In the Schrödinger wave mechanical model, Ψ²(r,θ,φ) represents the probability density of the electron.
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
ψ2=0 represent
View Solutionwave mechanical model of the atom depends upon:
View SolutionIn the Schrodinger's wave equation Ψ represents
View SolutionThe Schrodinger wave equation for hydrogen atom is Ψ2s=14√2π(1a0)3/2(2−ra0)e−r/a0 , where a0 is Bohr's radius . If the radial node in 2s be at r0 , then r0 would be equal to :
View SolutionIf x+iy=√ϕ+iy, where i=√−1 and ϕ and Ψ are non-zero real parameters, then ϕ and Ψ are constants, represents two system of rectangular hyperbola which intersect at an angle of :
View SolutionThe wave mechanical model of an atom is based upon which of the following equations ?
View SolutionThe wave mechanical model of an atom is based upon which of the following equations ?
View SolutionThe wave function ψn,l,m is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n,l and m. Here r is distance from nucleus θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.

For the given orbital in Column 1 the only Correct combination for any hydrogen -like species is
View SolutionThe wave function, Ψn,l,ml is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n, l and nl, Here r is distance from nucleus, θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.
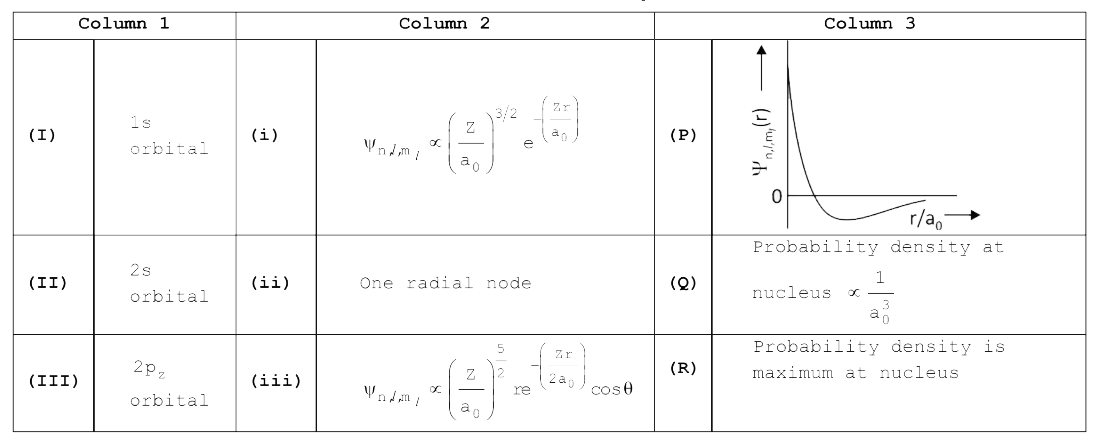
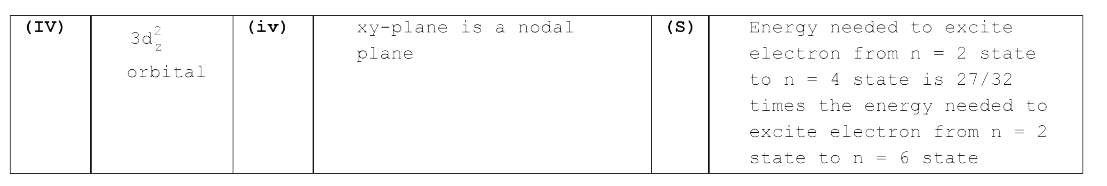
For hydrogen atom, the only CORRECT combination is:
View SolutionThe wave function, Ψn,l,ml is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n, l and nl, Here r is distance from nucleus, θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.

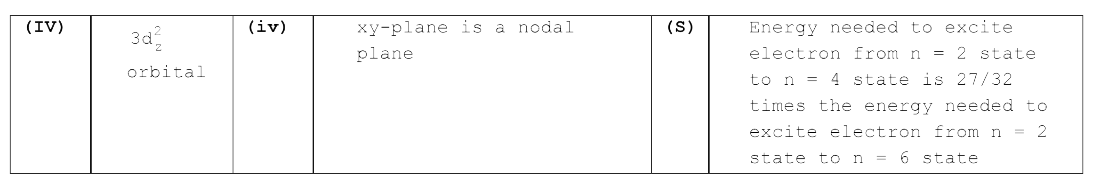
For the given orbital in Column 1, the only CORRECT combination for any hydrogen-like species is:
View Solution
