The energy of an electron of 2px orbital is :
greatern than 2pyorbital
less than 2pz orbital
equal to 2s orbital
same as that of 2pxand2pz orbital
The correct Answer is:D
To determine the energy of an electron in the 2p_x orbital, we need to analyze the quantum numbers associated with the orbital and apply the concept of n + l values.
1. Identify the Quantum Numbers:
- For the 2p_x orbital:
- The principal quantum number (n) is 2.
- The azimuthal quantum number (l) for p orbitals is 1.
2. Calculate the n + l Value:
- The n + l value for the 2p_x orbital is calculated as follows:
n+l=2+1=3
3. Calculate n + l for Other Orbitals:
- For the 2p_y orbital:
- n = 2, l = 1
n+l=2+1=3
- For the 2p_z orbital:
- n = 2, l = 1
n+l=2+1=3
- For the 2s orbital:
- n = 2, l = 0
n+l=2+0=2
4. Compare n + l Values:
- The n + l value for 2p_x, 2p_y, and 2p_z orbitals is 3, indicating that these orbitals are degenerate (they have the same energy).
- The n + l value for 2s is 2, which is lower than that of the p orbitals, indicating that the energy of the 2s orbital is lower than that of the 2p orbitals.
5. Conclusion:
- Since the n + l values for 2p_x, 2p_y, and 2p_z are the same, the energy of the electron in the 2p_x orbital is the same as that in the 2p_y and 2p_z orbitals.
- Therefore, the correct answer is that the energy of the electron in the 2p_x orbital is equal to that of the 2p_y and 2p_z orbitals.
Final Answer:
The energy of an electron in the 2p_x orbital is the same as that of the 2p_y and 2p_z orbitals.
---
- For the 2p_x orbital:
- The principal quantum number (n) is 2.
- The azimuthal quantum number (l) for p orbitals is 1.
- The n + l value for the 2p_x orbital is calculated as follows:
n+l=2+1=3
- For the 2p_y orbital:
- n = 2, l = 1
n+l=2+1=3
- For the 2p_z orbital:
- n = 2, l = 1
n+l=2+1=3
- For the 2s orbital:
- n = 2, l = 0
n+l=2+0=2
- The n + l value for 2p_x, 2p_y, and 2p_z orbitals is 3, indicating that these orbitals are degenerate (they have the same energy).
- The n + l value for 2s is 2, which is lower than that of the p orbitals, indicating that the energy of the 2s orbital is lower than that of the 2p orbitals.
- Since the n + l values for 2p_x, 2p_y, and 2p_z are the same, the energy of the electron in the 2p_x orbital is the same as that in the 2p_y and 2p_z orbitals.
- Therefore, the correct answer is that the energy of the electron in the 2p_x orbital is equal to that of the 2p_y and 2p_z orbitals.
The energy of an electron in the 2p_x orbital is the same as that of the 2p_y and 2p_z orbitals.
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
The energy of an electron of 2p1 orbital is
View SolutionThe energy of an electron in an atomic orbital of a multi electron atom depends on
View SolutionAccording to Bohr's model, if the kinetic energy of an electron in 2nd orbit of He+ is x, then what should be the ionisation energy of the electron revolving in 3rd orbit of M5+ ion
View SolutionAn electron is moving in 3rd orbit of Li+2 and its separation energy is y.The separation energy of an electron moving in 2nd orbit of He+ is
View SolutionThe energy of an electron in the 3rd orbit of an atom is −E. The energy of an electron in the first orbit will be
View SolutionThe energy of an electron in Bohr's orbit of hydrogen atom is −13.6eV. The total electronic energy of a hypothetical He atom in which there are no electron - electron repulsions or interactions is
View SolutionThe energy of an electron in first Bohr's orbit of H atom is −13.6eV. The energy value of electron in the first excited state of Li2+ is :
View SolutionOrbitals are the pictorial representationofΨ or Ψ2

Ψ2 tell about the probability of finding electron.
A 2px orbital is shown by given diagram
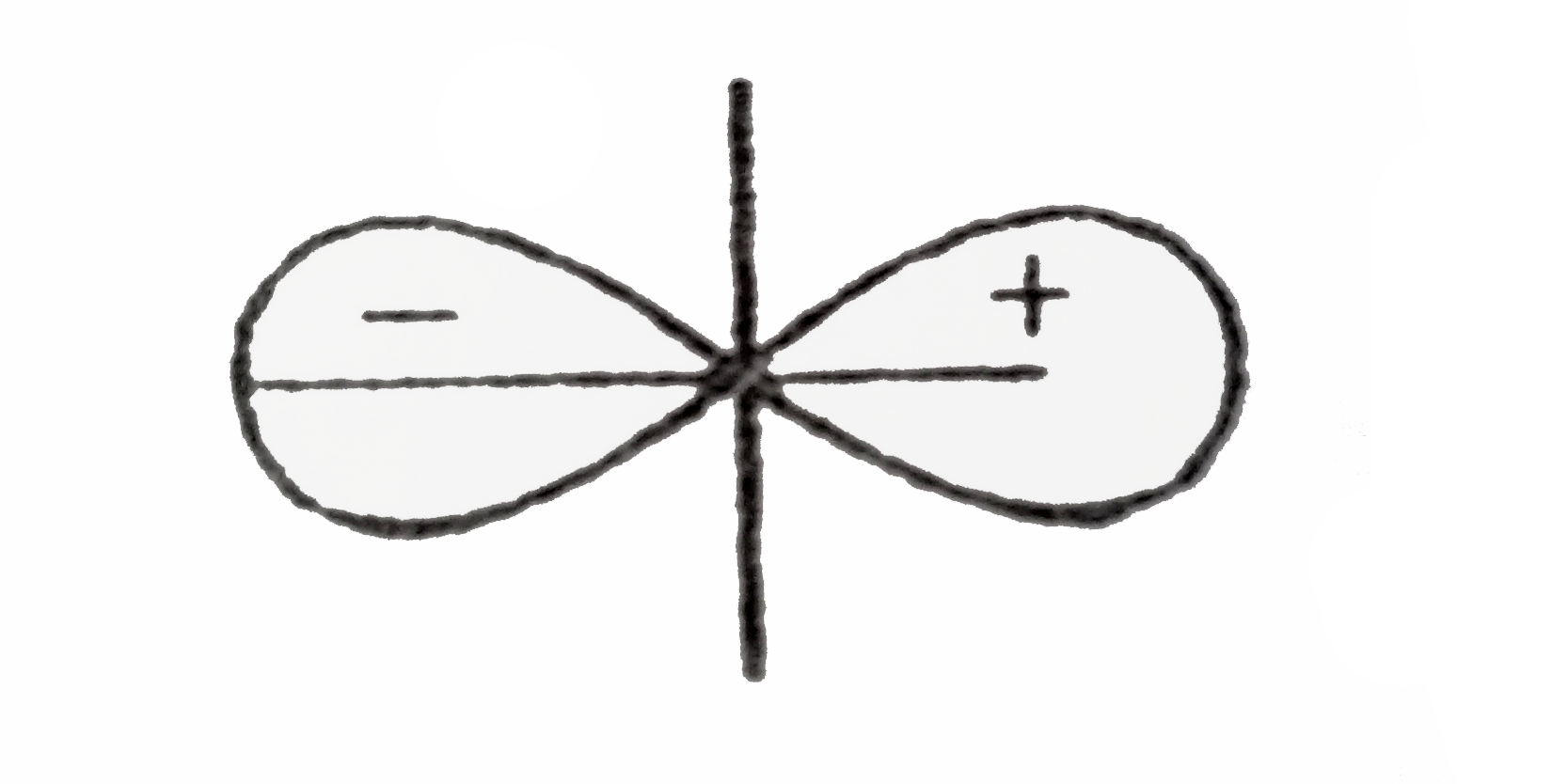
Correct regarding diagram is
View SolutionThe probability of finding the electron in px orbit is :
View SolutionWhich of the following statements is wrong? The probability of finding the electron in px orbital is
View Solution
