Calculate the value of A.
A=E1.22E2,1 where Enz= Emergy of electron in nth orbit, Z= atomic number of hydrogen like species.
To calculate the value of A where A=E1,22E2,1, we will use the formula for the energy of an electron in a hydrogen-like atom, which is given by:
En,z=−13.6Z2n2 eV
Step 1: Calculate E1,2
For E1,2, we have:
- n=1
- Z=2
Using the formula:
E1,2=−13.6×Z2n2=−13.6×2212=−13.6×41=−54.4 eV
Step 2: Calculate E2,1
For E2,1, we have:
- n=2
- Z=1
Using the formula:
E2,1=−13.6×Z2n2=−13.6×1222=−13.6×14=−3.4 eV
Step 3: Substitute values into the formula for A
Now we can substitute E1,2 and E2,1 into the equation for A:
A=E1,22E2,1=−54.42×(−3.4)
Step 4: Simplify the expression
Calculating the denominator:
2×(−3.4)=−6.8
Now substituting back into A:
A=−54.4−6.8=54.46.8
Step 5: Calculate the final value of A
Now performing the division:
A=8
Final Answer:
The value of A is 8.
---
- n=1
- Z=2
- n=2
- Z=1
Similar Questions
Knowledge Check
The angular speed of the electron in the nth Bohr orbit of the hydrogen atom is proportional to
Adirectly proportional to nBinversely proportional to √nCinversely proportional to n2Dinversely proportional to n3
If the potential energy of the electron in the first allowed orbit in hydrogen atom is E: its
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
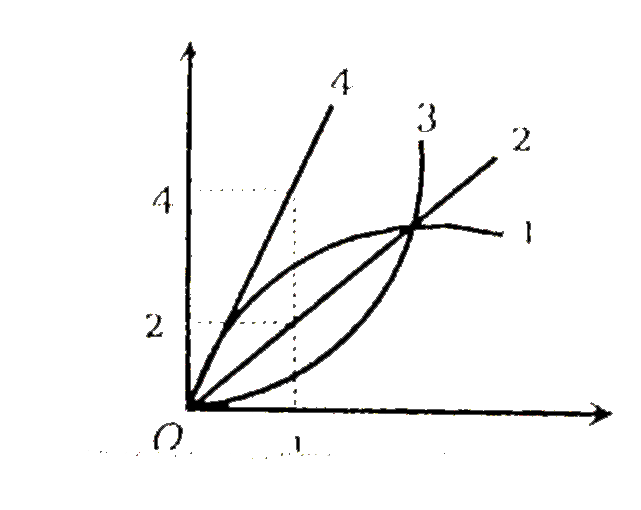
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
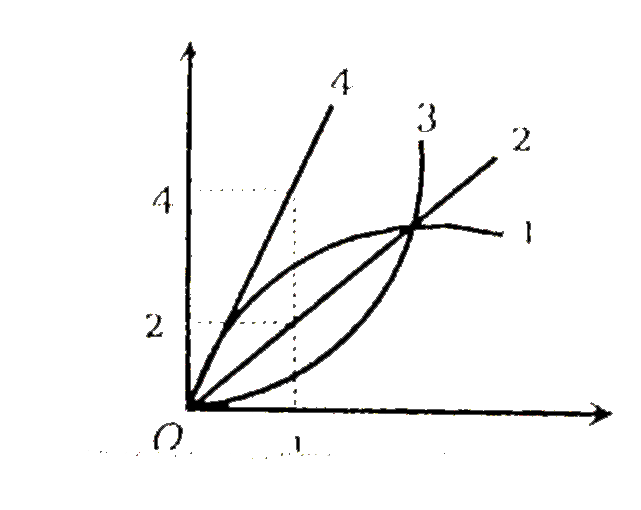
View SolutionIn the Bohr's model , for unielectronic species following symbols are used
rn,z→ Radius of nth orbit with atomic number "z"
Un,z→ Potential energy of electron in nth orbit with atomic number "z"
Kn,z→ Kinetic energy of electron in nth orbit with atomic number "z"
Vn,z→ Velocity of electon in nth orbit with atomic number "z"
Tn,z→ Time period of revolution of electon in nth orbit with atomic number "z"
Calculate z in all in cases.
(i)U1,2:K1,z=−8:9
(ii)r1,z:r2,1=1:12
(iii)v1,z:v3,1=15:1
(iv)T1,2:T2,z=9:32
Report your answer as (2r-p-q-s) where p,q,r and s represents the value of "z" in parts (i),(ii),(iii),(iv).
View SolutionWhich of the following option(s) is/are independent of both n and Z for H−like species?
Un= Potential energy of electron in nth orbit
KEn= Kinetic energy of electron in nth orbit
ln= Angular momentam of electoron in nth orbit
vn= Velcity of electron in nth orbit
fn= Frequency of electron in nth orbit
Tn= Time period of revolution of electron in nth orbit
View SolutionIn hydrogen atom, if the difference in the energy of the electron in n=2 and n=3 orbits is E, the ionization energy of hydrogen atom is
View SolutionHydrogen atom:
The electronic ground state of hydrogen atom contains one electron in the first orbit. If sufficient energy is provided, this electron can be promoted to higher energy levels. The electronic energy of a hydrogen-like species (any atom//ions with nuclear charge Z and one electron) can be given as
En=−RHZ2n2 where RH=Rydberg constant,n=principal quantum number
Calculate the following :
(a) the kinetic energy (in eV) of an electron in the ground state of hydrogen atom.
(b) the potential energy (in eV) of an electron in the ground state of hydrogen atom.
View Solution
