In a concentration cell the same reagents are present in both the anode and the cathode compartments , but at different concentrations. Calculate the emf of a cell of a cell containing 0.040 M. Cr3+ in one compartment and 1.0 M Cr3+ in the other if Cr electrodes are used in both.
0.028 V
0.249 V
0.083 V
0.125 V
The correct Answer is:A
To calculate the emf of a concentration cell containing different concentrations of Cr3+, we can follow these steps:
Step 1: Write the cell representation
The cell consists of chromium electrodes in two compartments with different concentrations of Cr3+. The cell representation is:
\( \text{Cr (s)} | \text{Cr}^{3+} (0.04 \, M) || \text{Cr}^{3+} (1.0 \, M) | \text{Cr (s)} \)
Step 2: Identify the anode and cathode
In a concentration cell:
- The anode is where oxidation occurs (lower concentration).
- The cathode is where reduction occurs (higher concentration).
Thus:
- Anode: Cr(s) → Cr3+(aq) + 3e⁻ (0.04 M)
- Cathode: Cr3+(aq) + 3e⁻ → Cr(s) (1.0 M)
Step 3: Write the half-reactions
The half-reactions are:
1. Oxidation (at anode):
\( \text{Cr (s)} \rightarrow \text{Cr}^{3+} (aq) + 3e^- \)
2. Reduction (at cathode):
\( \text{Cr}^{3+} (aq) + 3e^- \rightarrow \text{Cr (s)} \)
Step 4: Write the overall cell reaction
Combining the half-reactions, we have:
\( \text{Cr (s)} + \text{Cr}^{3+} (1.0 \, M) \rightarrow \text{Cr}^{3+} (0.04 \, M) + \text{Cr (s)} \)
Step 5: Use the Nernst equation
The Nernst equation is given by:
\( E_{cell} = E^0_{cell} - \frac{0.0591}{n} \log Q \)
Where:
- \( E^0_{cell} \) is the standard cell potential (0 for the same metal),
- \( n \) is the number of moles of electrons transferred (3 for chromium),
- \( Q \) is the reaction quotient.
Step 6: Calculate the reaction quotient (Q)
The reaction quotient \( Q \) is given by:
\( Q = \frac{(\text{Cr}^{3+})_{products}}{(\text{Cr}^{3+})_{reactants}} = \frac{0.04}{1.0} = 0.04 \)
Step 7: Substitute values into the Nernst equation
Since \( E^0_{cell} = 0 \):
\( E_{cell} = 0 - \frac{0.0591}{3} \log(0.04) \)
Step 8: Calculate \( \log(0.04) \)
Using logarithmic properties:
\( \log(0.04) = \log(4) - \log(100) = 0.602 - 2 = -1.398 \)
Step 9: Substitute \( \log(0.04) \) back into the equation
\( E_{cell} = -\frac{0.0591}{3} \times (-1.398) \)
Step 10: Calculate the final value
\( E_{cell} = \frac{0.0591 \times 1.398}{3} \)
\( E_{cell} = \frac{0.0826}{3} \approx 0.0275 \, V \)
Step 11: Round the answer
Rounding gives:
\( E_{cell} \approx 0.028 \, V \)
Thus, the emf of the cell is approximately 0.028 volts.
---
The cell consists of chromium electrodes in two compartments with different concentrations of Cr3+. The cell representation is:
\( \text{Cr (s)} | \text{Cr}^{3+} (0.04 \, M) || \text{Cr}^{3+} (1.0 \, M) | \text{Cr (s)} \)
In a concentration cell:
- The anode is where oxidation occurs (lower concentration).
- The cathode is where reduction occurs (higher concentration).
- Anode: Cr(s) → Cr3+(aq) + 3e⁻ (0.04 M)
- Cathode: Cr3+(aq) + 3e⁻ → Cr(s) (1.0 M)
The half-reactions are:
1. Oxidation (at anode):
\( \text{Cr (s)} \rightarrow \text{Cr}^{3+} (aq) + 3e^- \)
2. Reduction (at cathode):
\( \text{Cr}^{3+} (aq) + 3e^- \rightarrow \text{Cr (s)} \)
Combining the half-reactions, we have:
\( \text{Cr (s)} + \text{Cr}^{3+} (1.0 \, M) \rightarrow \text{Cr}^{3+} (0.04 \, M) + \text{Cr (s)} \)
The Nernst equation is given by:
\( E_{cell} = E^0_{cell} - \frac{0.0591}{n} \log Q \)
- \( E^0_{cell} \) is the standard cell potential (0 for the same metal),
- \( n \) is the number of moles of electrons transferred (3 for chromium),
- \( Q \) is the reaction quotient.
The reaction quotient \( Q \) is given by:
\( Q = \frac{(\text{Cr}^{3+})_{products}}{(\text{Cr}^{3+})_{reactants}} = \frac{0.04}{1.0} = 0.04 \)
Since \( E^0_{cell} = 0 \):
\( E_{cell} = 0 - \frac{0.0591}{3} \log(0.04) \)
Using logarithmic properties:
\( \log(0.04) = \log(4) - \log(100) = 0.602 - 2 = -1.398 \)
\( E_{cell} = -\frac{0.0591}{3} \times (-1.398) \)
\( E_{cell} = \frac{0.0591 \times 1.398}{3} \)
\( E_{cell} = \frac{0.0826}{3} \approx 0.0275 \, V \)
Rounding gives:
\( E_{cell} \approx 0.028 \, V \)
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - LEVEL-228videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - LEVEL-337videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - DILUTE SOLUTIONEXERCISE - leval-0323videos
DILUTE SOLUTION
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Subjective problems15videos
GASEOUS STATE
Similar Questions
Consider the following Galvanic cell:-

By what value the cell voltage when concentration of ions in anodic and cathodic compartments both increased by factor of 10 at 298K:View SolutionWhat type of a battery is lead storage battery? Write the anode and cathode reactions and the overall cell reaction occurring in the operation of a lead storage battery.
(b) Calucluate the potential for half-cell containing.
0.10 M K2Cr2O7(aq),0.20MCr3+(aq)and1.0×10−4MH+(aq)
The half -cell reaction is
Cr2O2−7(aq)+4H+(aq)+6e−→2Cr3+(aq)+7H2O(l)
and the standard electron potential is given as Eo=1.33V.View Solution
Knowledge Check
- Question 1 - Select One
When a cell is placed in 0.5 M solution of salt and no change in the volume of the cell is observed, the concentration of cell sap would be
A0.5 MB0.05 MC5.0 MD50 M
Given concentration cell Zn/Zn2+(1M)/Zn2+(0.15M)/Z
Calculate E cell. As the cell discharges, does the difference in concentrations between the two solutions become smaller or larger?View SolutionCalculate the emf of the following cell at 25∘C
Ag(s)|AgNO3(0.01M)||AgNO3(0.05M)|Ag(s)View SolutionA cell diagram shown below contains of one litre of buffer solution of HA(PKa=4) and NaA in both compartments. What is the cell e.m.f?
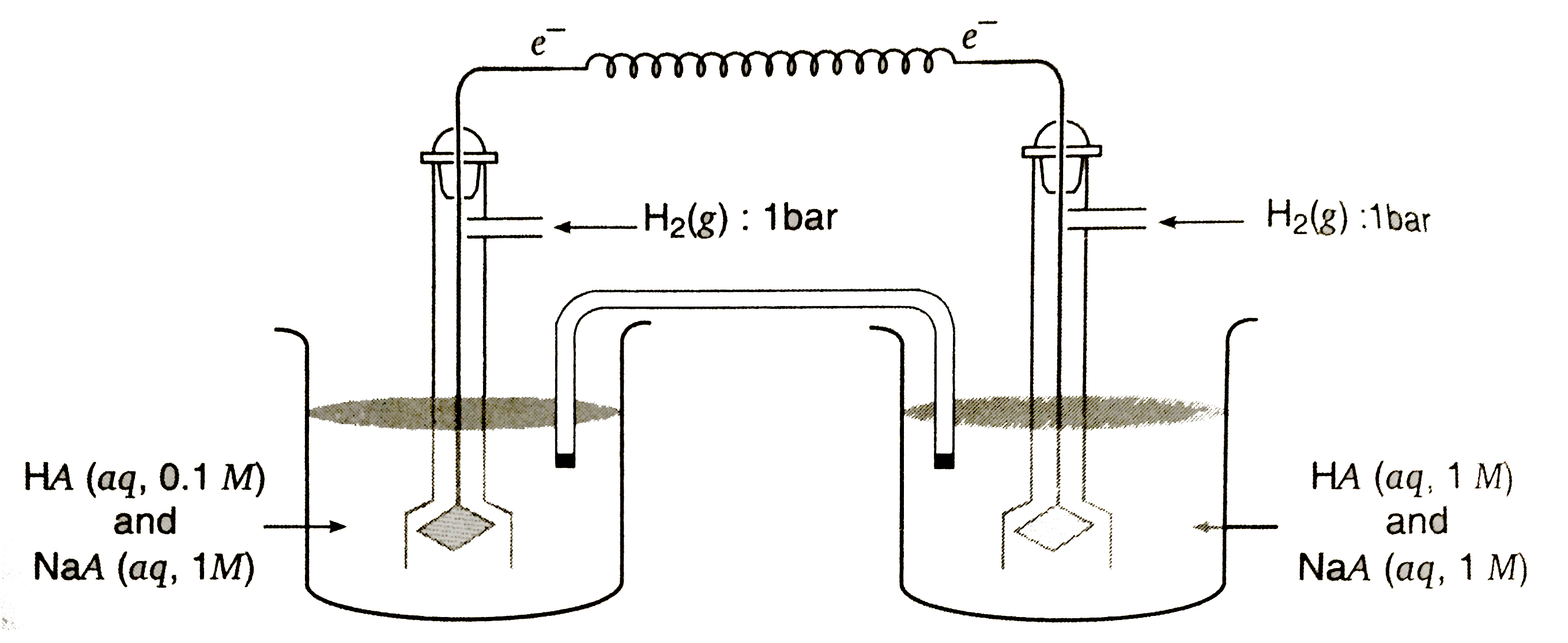 View Solution
View SolutionA concentration cell Pt|H2(g)|HCl(aq)||H2SO4(aq)|H2(g)|Pt is constructed using equal concentration of acids and equal number of moles of H2 gas in both the compartments at the same temperature.If volume of H2 gas at the anodic compartment is 19 times the volume of H2 gas at cathodic compartment Which of the following is/are correct for the given cell (log2=0.3,log3=0.48)2.303RTF=0.06V
View SolutionThe cell consists of three compartments separated by porous barriers. The first contains a cobalt electrode in 5.00 L of 0.100 M cobalt (II) nitrate, the second contains 5.00 L of 0.100M AgNO3. Assuming that the current within the cell is carried equally by the positive and negative ions, tabulate the concentrations of ions of each type in each compartment of the cell after the passage of 0.100 mole electrons.
given Co2++2e−→Co E0=−0.28V
Ag++e−→Ag E0=0.80V
Spontaneous reaction is: 2Ag++Co2++2Ag 1.08VView SolutionCalculate the EMF of a Daniel cell when the concentartion of ZnSO4 and CuSO4 are 0.001M and 0.1M respectively. The standard potential of the cell is 1.1V.
View SolutionA cell contains two hydrogen electrodes. The negative electrode is in contact with a solution of 10−6M hydrogen ions. The EMF of the cell is 0.118V at 25∘C. Calculate the concentration of hydrogen ions at the positive electrode.
View Solution

