The E∘ at 25∘C for the following reaction at the indicated concentrations is 1.50 V. Calculate the ΔG in kJ/mol 25∘C :
−140.94
−295
−212
−422.83
The correct Answer is:D
To calculate the Gibbs free energy change (ΔG) for the given electrochemical reaction at 25°C, we can follow these steps:
Step 1: Write down the reaction
The reaction is:
Cr (s)+3Ag+(aq)→3Ag (s)+Cr3+(aq)
Step 2: Identify the number of electrons transferred (n)
In this reaction, chromium (Cr) is oxidized from an oxidation state of 0 to +3, losing 3 electrons. Silver ions (Ag⁺) are reduced from +1 to 0, gaining 3 electrons. Therefore, the number of electrons transferred (n) is:
n=3
Step 3: Use the Nernst equation
The Nernst equation relates the standard cell potential (E°) to the cell potential (E) under non-standard conditions:
E=E°−0.059nlog((Cr3+)(Ag+)3)
Given:
- E°=1.50V
- (Cr3+)=0.1M
- (Ag+)=0.1M
Step 4: Substitute values into the Nernst equation
Substituting the known values into the Nernst equation:
E=1.50−0.0593log(0.1(0.1)3)
Step 5: Simplify the logarithm
The logarithm simplifies as follows:
log(0.1(0.1)3)=log(0.1)−log(0.13)=log(0.1)−3log(0.1)=−1+3=2
Step 6: Calculate E
Now substituting back into the equation:
E=1.50−0.0593×2
E=1.50−0.059×23
E=1.50−0.03933
E≈1.46067V
Step 7: Calculate ΔG using the formula
The Gibbs free energy change can be calculated using the formula:
ΔG=−nFE
Where:
- F (Faraday's constant) = 96500 C/mol
Substituting the values:
ΔG=−3×96500×1.46067
Step 8: Calculate ΔG
Calculating this gives:
ΔG=−3×96500×1.46067≈−422843.7J/mol
Step 9: Convert to kJ/mol
To convert from joules to kilojoules:
ΔG≈−422.8437kJ/mol
Final Answer
Thus, the Gibbs free energy change (ΔG) is approximately:
ΔG≈−422.84kJ/mol
The reaction is:
Cr (s)+3Ag+(aq)→3Ag (s)+Cr3+(aq)
In this reaction, chromium (Cr) is oxidized from an oxidation state of 0 to +3, losing 3 electrons. Silver ions (Ag⁺) are reduced from +1 to 0, gaining 3 electrons. Therefore, the number of electrons transferred (n) is:
n=3
The Nernst equation relates the standard cell potential (E°) to the cell potential (E) under non-standard conditions:
E=E°−0.059nlog((Cr3+)(Ag+)3)
- E°=1.50V
- (Cr3+)=0.1M
- (Ag+)=0.1M
Substituting the known values into the Nernst equation:
E=1.50−0.0593log(0.1(0.1)3)
The logarithm simplifies as follows:
log(0.1(0.1)3)=log(0.1)−log(0.13)=log(0.1)−3log(0.1)=−1+3=2
Now substituting back into the equation:
E=1.50−0.0593×2
E=1.50−0.059×23
E=1.50−0.03933
E≈1.46067V
The Gibbs free energy change can be calculated using the formula:
ΔG=−nFE
Where:
- F (Faraday's constant) = 96500 C/mol
ΔG=−3×96500×1.46067
Calculating this gives:
ΔG=−3×96500×1.46067≈−422843.7J/mol
To convert from joules to kilojoules:
ΔG≈−422.8437kJ/mol
Thus, the Gibbs free energy change (ΔG) is approximately:
ΔG≈−422.84kJ/mol
Topper's Solved these Questions
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - LEVEL-2
28 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - LEVEL-3
37 Videos
- DILUTE SOLUTIONBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - DILUTE SOLUTIONEXERCISE - leval-03
23 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Subjective problems
15 Videos
Similar Questions
Knowledge Check
A first order reaction is 50% completed in 30min at 27∘C and in 10min at 47∘C. Calculate the reaction rate constants at 27∘C and the energy of activation of the reaction in kJmol−1.
Ak=0.0231min−1,Ea=43.848kJmol−1Bk=0.017min−1,Ea=52.54kJmol−1Ck=0.0693min−1,Ea=43.848kJmol−1Dk=0.0231min−1,Ea=28.92kJmol−1
The measured voltage for the reaction with the indicated concentration is 1.50 V. Calculate E∘.
Cr(s)+3Ag+(aq,0.10M)→3Ag(s)+Cr3+(aq,0.30M)
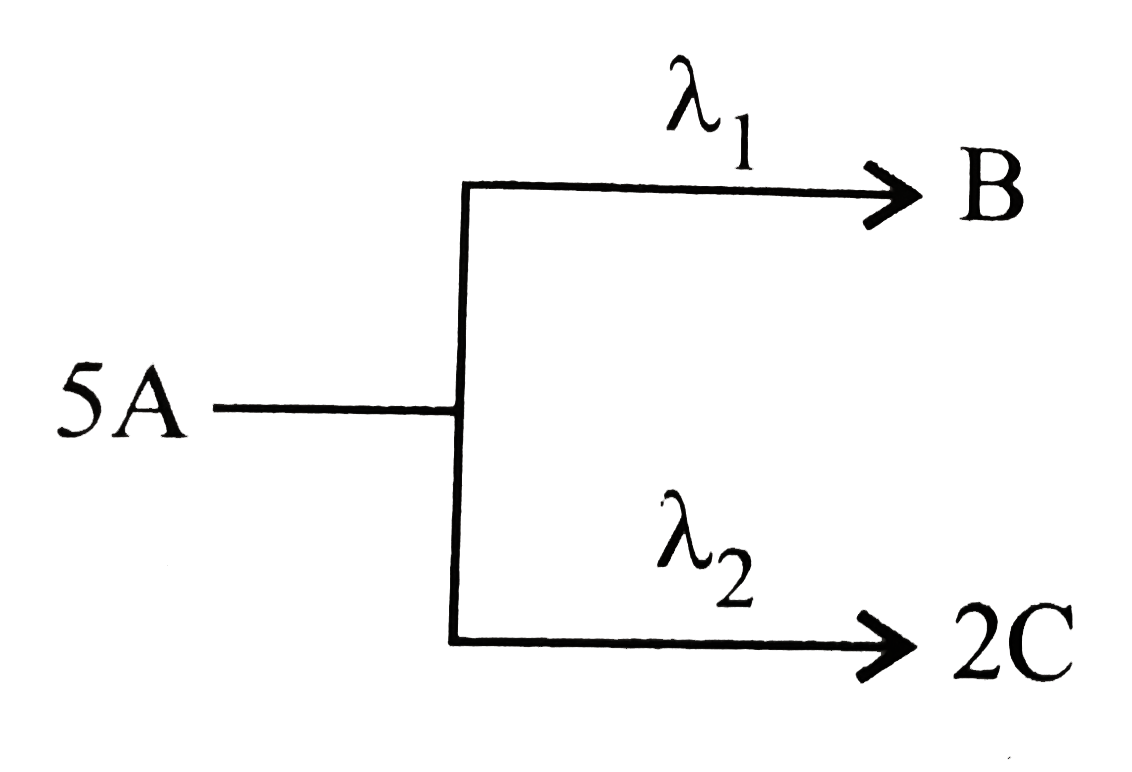
View SolutionA follow parallel path of first-order reactions giving B and C as
If the initial concentration of A is 0.25M, calculate the concentration of C after 5 hr of reaction.
View SolutionFor the cell Zn|ZnCl2(m)|AgCl,E is 1.24V at 25∘C and 1.260V at 35∘C of m=10−3. Write down the cell reaction and calculate ΔG,ΔH, and ΔS at 25∘C.
View SolutionThe standard free energy change for a reaction is −213.3KJmol−1at25∘C. If the enthalpy change of the reaction is −217.77KJmole−1 . Calculate the magnitude of entropy change for the reaction in Joule mole−1
View SolutionFor the reaction A→ Products, it is found that the rate of reaction increases by a factor of 6.25 when concentration of A increases by a factor of 2.5. Calculate the order of reaction with respect to A.
View SolutionFor a cell reaction ΔG∘=−1930kJmol and the cell e.m.f (E∘) at standard condition is 2.5 V. What is value of ΔG∘2FE∘?
View SolutionThe standard potential of a cell using the reaction
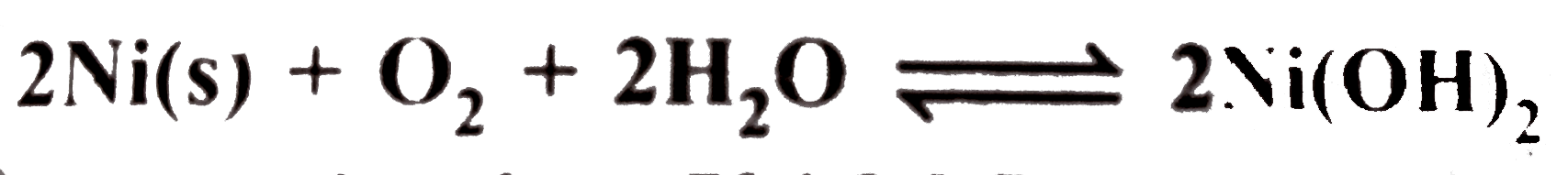 is 1.12. The heat of the reaction is −504.2kJmol−1 at 25∘C. Calculate the entropy change.
is 1.12. The heat of the reaction is −504.2kJmol−1 at 25∘C. Calculate the entropy change.
View Solution
