A conducting sphere is enclosed by a hollow conducting shell. Initially the inner sphere has a charge Q while the outer one is uncharged. The potential difference between the two spherical surface is found to be V. later on the outer shell is given a charge -4Q. The new potential difference between the two surfaces is : (A) V (B) −V (C) −2V (D) 2V
To solve the problem, we will analyze the situation step by step.
Step 1: Understand the initial configuration
We have a conducting sphere with charge Q and a hollow conducting shell that is initially uncharged. The potential difference V between the surfaces of the inner sphere and the outer shell is given.
Step 2: Determine the initial potential difference
The potential V1 at the surface of the inner sphere (radius a) due to its charge Q is given by:
V1=Q4πϵ0a
The potential V2 at the surface of the outer shell (radius b) is zero because it is uncharged and the electric field inside a conductor in electrostatic equilibrium is zero. Therefore, the potential difference V between the two surfaces is:
V=V1−V2=Q4πϵ0a−0=Q4πϵ0a
Step 3: Analyze the new configuration after charging the outer shell
Now, the outer shell is given a charge of −4Q. According to electrostatic shielding, the charge on the outer shell does not affect the charge distribution on the inner sphere. The inner sphere still has charge Q.
Step 4: Determine the new potential at the outer shell
When the outer shell has a charge of −4Q, it will induce a charge of +4Q on the inner surface of the shell. The outer surface of the shell will then have a charge of −4Q (the total charge on the shell remains the same).
The potential V′2 at the surface of the outer shell (radius b) due to the charge −4Q is:
V′2=−4Q4πϵ0b
Step 5: Calculate the new potential difference
The new potential difference V′ between the inner sphere and the outer shell is given by:
V′=V1−V′2=Q4πϵ0a−(−4Q4πϵ0b)
This simplifies to:
V′=Q4πϵ0a+4Q4πϵ0b
Step 6: Relate the new potential difference to the initial potential difference
From the initial potential difference V=Q4πϵ0a, we can express the new potential difference as:
V′=V+4Q4πϵ0b
Since the term 4Q4πϵ0b is a positive contribution, the new potential difference V′ will be greater than the initial potential difference V.
Conclusion
Thus, the new potential difference between the two surfaces is:
V′=V+positive term
This indicates that the potential difference has increased, and we can conclude that the answer is:
New potential difference=2V
Final Answer
The correct option is (D) 2V.
We have a conducting sphere with charge Q and a hollow conducting shell that is initially uncharged. The potential difference V between the surfaces of the inner sphere and the outer shell is given.
The potential V1 at the surface of the inner sphere (radius a) due to its charge Q is given by:
V1=Q4πϵ0a
The potential V2 at the surface of the outer shell (radius b) is zero because it is uncharged and the electric field inside a conductor in electrostatic equilibrium is zero. Therefore, the potential difference V between the two surfaces is:
V=V1−V2=Q4πϵ0a−0=Q4πϵ0a
Now, the outer shell is given a charge of −4Q. According to electrostatic shielding, the charge on the outer shell does not affect the charge distribution on the inner sphere. The inner sphere still has charge Q.
When the outer shell has a charge of −4Q, it will induce a charge of +4Q on the inner surface of the shell. The outer surface of the shell will then have a charge of −4Q (the total charge on the shell remains the same).
V′2=−4Q4πϵ0b
The new potential difference V′ between the inner sphere and the outer shell is given by:
V′=V1−V′2=Q4πϵ0a−(−4Q4πϵ0b)
This simplifies to:
V′=Q4πϵ0a+4Q4πϵ0b
From the initial potential difference V=Q4πϵ0a, we can express the new potential difference as:
V′=V+4Q4πϵ0b
Since the term 4Q4πϵ0b is a positive contribution, the new potential difference V′ will be greater than the initial potential difference V.
Thus, the new potential difference between the two surfaces is:
V′=V+positive term
This indicates that the potential difference has increased, and we can conclude that the answer is:
New potential difference=2V
The correct option is (D) 2V.
Similar Questions
A conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionA solid conducting sphere, having a charge Q, is surrounded by an unchanged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a change of −4Q, the new potential difference between the same tow surface is :
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2.
Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionIn the given figure there are two concentric shells find potential difference between spheres.
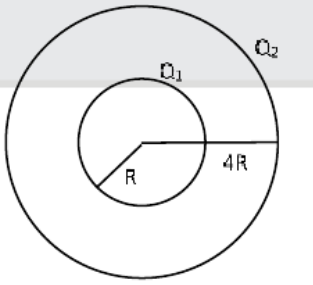
View SolutionA solid conducting sphere of radius a is enclosed in a concentric shell of radius b>a. The charge on the inner sphere is 3μC and on the conducting shell is −10μC. The potential difference between the conductors is V. If +10μC additional charge is given to the outer shell, the new potential difference is
A. V
B. V/2
C. 2V
D. zero
View SolutionIn (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionTwo hollow concentric non-conducting spheres of radius the a and b(a>b) contain charges Qa and Qb respectively. Prove that potential difference between the two spheres is independent of charge on outer sphere. If outer sphere is given an extra charge, is there any change in potential difference ?
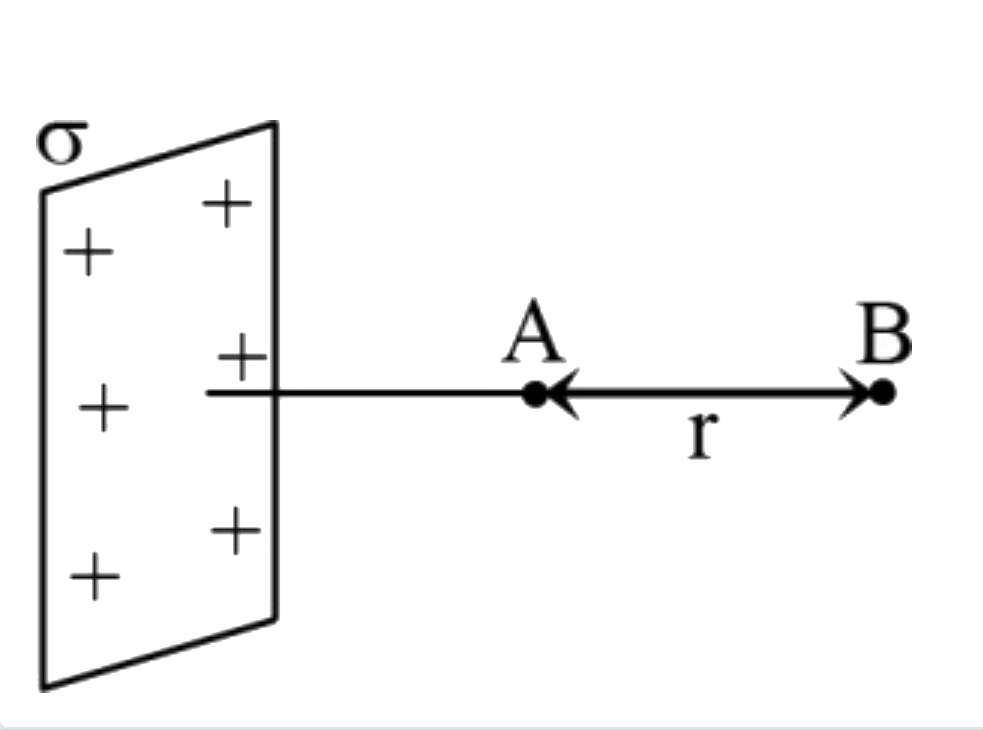
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
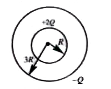
What would be the final distribution of charges if the sphres are joined by a conducting wire
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View Solution
