Question

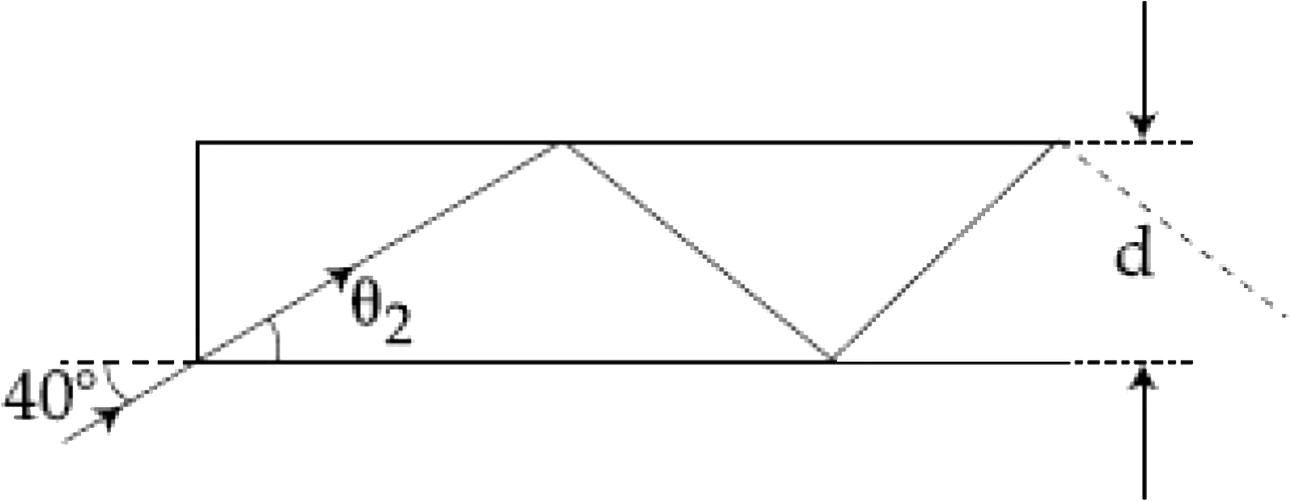
Find out no. of reflection after which right Ray will exit from (Given ${\sin 40}^{\circ }=0.64$) (A) 130000 (B) 57803 (C) 140000 (D) 150000

Explanation

To solve the problem of finding the number of reflections after which a light ray will exit from a medium with given parameters, we can follow these steps:

Step 1: Identify the given data
- Refractive index of the medium (n1) = 1.31
- Refractive index of air (n2) = 1
- Angle of incidence (i) = 40 degrees
- Given: sin(40 degrees) = 0.64

Step 2: Use Snell's Law to find the angle of refraction (R)
According to Snell's Law:
\( n_1 \cdot \sin(i) = n_2 \cdot \sin(R) \)
Substituting the known values:
\( 1.31 \cdot \sin(40^\circ) = 1 \cdot \sin(R) \)
\( 1.31 \cdot 0.64 = \sin(R) \)
Calculating this gives:
\( \sin(R) = 0.8384 \)
Now, we find R:
\( R = \sin^{-1}(0.8384) \approx 57.5^\circ \)

Step 3: Calculate the critical angle (θc)
The critical angle can be calculated using:
\( n_1 \cdot \sin(\theta_c) = n_2 \cdot \sin(90^\circ) \)
\( 1.31 \cdot \sin(\theta_c) = 1 \cdot 1 \)
\( \sin(\theta_c) = \frac{1}{1.31} \approx 0.7634 \)
Calculating the critical angle:
\( \theta_c = \sin^{-1}(0.7634) \approx 49.5^\circ \)

Step 4: Determine if total internal reflection occurs
Since the angle of incidence (i = 40 degrees) is greater than the critical angle (θc ≈ 49.5 degrees), total internal reflection will occur.

Step 5: Calculate the distance between reflections
Using the geometry of the situation, we can find the distance (d) between the reflections. The distance can be calculated using:
\( \tan(R) = \frac{h}{d} \)
Where h is the height of the triangle formed by the reflections. For a triangle with an angle of 30 degrees:
\( \tan(30^\circ) = \frac{h}{d} \)
From geometry, we can express:
\( d = \frac{h}{\tan(30^\circ)} = h \cdot \sqrt{3} \)

Step 6: Calculate the number of reflections in a given length
If we consider a length of 2 meters (2000 mm) of the medium, we can find the number of reflections (N) using the formula:
\( N = \frac{L}{d} \)
Where L is the total length of the medium.

Step 7: Substitute the values to find N
Using the previously calculated distance between reflections, we can find:
\( N = \frac{2000 \, \text{mm}}{20 \sqrt{3} \times 10^{-6} \, \text{m}} \)
Calculating this gives:
\( N \approx 57803 \)

Conclusion
Thus, the number of reflections after which the light ray will exit from the medium is approximately 57803.