Calculate ΔU if 2kJ heat is released and 10kJ work is done on the system.
12kJ
8kJ
−8kJ
−12kJ
The correct Answer is:B
To calculate the change in internal energy (ΔU) of the system, we can use the first law of thermodynamics, which is expressed as:
ΔU=Q+W
where:
- ΔU is the change in internal energy,
- Q is the heat added to the system, and
- W is the work done on the system.
1. Identify the heat (Q) released:
- The problem states that 2 kJ of heat is released. Since heat is released, it is considered negative in the context of the system.
- Therefore, Q=−2kJ.
2. Identify the work (W) done on the system:
- The problem states that 10 kJ of work is done on the system. Work done on the system is considered positive.
- Therefore, W=+10kJ.
3. Apply the first law of thermodynamics:
- Substitute the values of Q and W into the equation:
ΔU=Q+W=(−2kJ)+(10kJ)
4. Perform the calculation:
- Calculate ΔU:
ΔU=−2+10=8kJ
5. Final Result:
- The change in internal energy ΔU is 8kJ.
Summary:
The change in internal energy of the system is ΔU=8kJ.
- ΔU is the change in internal energy,
- Q is the heat added to the system, and
- W is the work done on the system.
- The problem states that 2 kJ of heat is released. Since heat is released, it is considered negative in the context of the system.
- Therefore, Q=−2kJ.
- The problem states that 10 kJ of work is done on the system. Work done on the system is considered positive.
- Therefore, W=+10kJ.
- Substitute the values of Q and W into the equation:
ΔU=Q+W=(−2kJ)+(10kJ)
- Calculate ΔU:
ΔU=−2+10=8kJ
- The change in internal energy ΔU is 8kJ.
The change in internal energy of the system is ΔU=8kJ.
Topper's Solved these Questions
Similar Questions
In a reaction 2.5KJ of heat is released from the system and 5.5 KJ of work is done on the system.Calculate 'DeltaU'.
View SolutionWhen a system is taken from A to C through path ABC, 10 J of heat flows to the system and 4 J of work is done by the system.
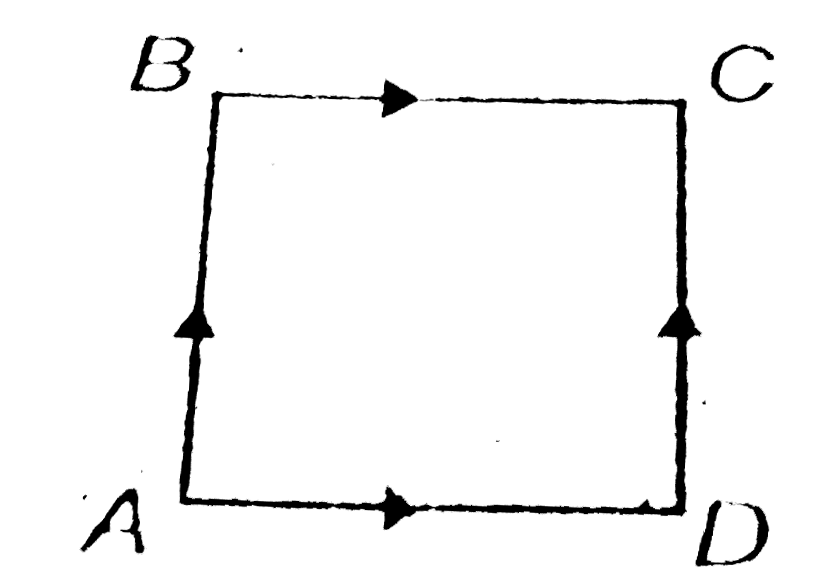
How much heat flows into the system in path ADC, if the work done by the system is 3 J ?
View Solution
Knowledge Check
What will be the change in internal energy when 12 kJ of work is done on the system and 2 kJ of heat is given by the system?
A+10kJB−10kJC+5kJD−5kJ
A gas can be ken from A to B via two different processes ACB and ADB. When path ACB is used 60 J of heat flows into the system and 30 J of work is done by the system. If path ADB is used work done by the system is 10 J. The heat Flow into the system in path ADB is :

View SolutionCalculate the changes in internal energy of a system if,
300 J of heat energy is added to the system and a work of 160 J is done on the system.
View SolutionWhat is the change in internal energy if 10 J of heat is given to system at constant pressure and 20 J of work is done by the system?
View SolutionCalculate the internal energy change in each of the following cases .
(a) A system absorbs 5kJ of heat and does 1kJ of work
(b) 5kJ of work is done on the system amd 1kJ of heat is given out by the system .
View SolutionIn given figure, let ΔU1 and ΔU2 be change in internal energy in process ABC and CDA respectively. ΔQ and W be the net heta given and net work done by the system in the process ABC+CDA, then

View SolutionFor a gaseous state if heat supplied to the system is 100 J and work done by the system is 25 J. then internal energy of the system is
View SolutionIf ΔU and ΔW represent the increase in internal energy and work done by the system resectively in a thermodynamical process, which of the following is true?
View Solution
