→r=15t2i+(20−20t2)j
find magnitude of acceleration at t=1 sec.
30m/s2
40m/s2
70m/s2
50m/s2
The correct Answer is:D
To find the magnitude of the acceleration at t=1 second for the given position vector →r=15t2^i+(20−20t2)^j, we will follow these steps:
Step 1: Differentiate the position vector to find the velocity vector.
The position vector is given as:
→r=15t2^i+(20−20t2)^j
To find the velocity vector →v, we differentiate →r with respect to time t:
→v=d→rdt=ddt(15t2)^i+ddt(20−20t2)^j
Calculating the derivatives:
- For the ^i component:
ddt(15t2)=30t
- For the ^j component:
ddt(20−20t2)=0−40t=−40t
Thus, the velocity vector is:
→v=30t^i−40t^j
Step 2: Differentiate the velocity vector to find the acceleration vector.
Next, we find the acceleration vector →a by differentiating the velocity vector:
→a=d→vdt=ddt(30t)^i+ddt(−40t)^j
Calculating the derivatives:
- For the ^i component:
ddt(30t)=30
- For the ^j component:
ddt(−40t)=−40
Thus, the acceleration vector is:
→a=30^i−40^j
Step 3: Calculate the magnitude of the acceleration vector.
The magnitude of the acceleration vector |→a| is given by:
|→a|=√(30)2+(−40)2
Calculating:
|→a|=√900+1600=√2500=50m/s2
Conclusion
The magnitude of the acceleration at t=1 second is:
50m/s2
The position vector is given as:
→r=15t2^i+(20−20t2)^j
→v=d→rdt=ddt(15t2)^i+ddt(20−20t2)^j
- For the ^i component:
ddt(15t2)=30t
- For the ^j component:
ddt(20−20t2)=0−40t=−40t
→v=30t^i−40t^j
Next, we find the acceleration vector →a by differentiating the velocity vector:
→a=d→vdt=ddt(30t)^i+ddt(−40t)^j
- For the ^i component:
ddt(30t)=30
- For the ^j component:
ddt(−40t)=−40
→a=30^i−40^j
The magnitude of the acceleration vector |→a| is given by:
|→a|=√(30)2+(−40)2
|→a|=√900+1600=√2500=50m/s2
The magnitude of the acceleration at t=1 second is:
50m/s2
Topper's Solved these Questions
Similar Questions
The position vector of a particle changes with time according to the direction →r(t)=15t2ˆi+(4−20t2)ˆj. What is the magnitude of the acceleration at t=1?
View SolutionIf v=(t2−4t+105)m/s where t is in second. Find acceleration at t=1 sec.
View SolutionA particle moves in circle of radius 1.0 cm at a speed given by v=2.0 t where v is in cm/s and t in seconeds. A. find the radia accelerationof the particle at t=1 s. b. Findthe tangential acceleration at t=1s. c.Find the magnitude of the aceleration at t=1s.
View SolutionThe velocity of a particle is given by v=(2t2−3t+10)ms−1. Find the instantaneous acceleration at t = 5 s.
View SolutionIf v=(t+2)(t+3) then acceleration(i.edvdt) at t=1 sec.
View SolutionIf →A=2ˆi+ˆj+ˆk and →B=ˆi+2ˆj+2ˆk, find the magnitude of compinent of (→A+→B) along →B
View SolutionIf s=2t3+3t2+2t+8 then find time at which acceleration is zero.
View SolutionA particle is moving with a velocity of →v=(3ˆi+4tˆj)m/s. Find the ratio of rangential acceleration to that of total acceleration at t=1sec
View SolutionA particle has initial velocity (2→i+3→j) and acceleration (0.3→i+0.2→j). The magnitude of velocity after 10 seconds will be
View SolutionFigure given here shows the variation of velocity of a particle with time.
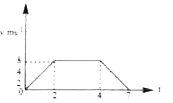
Find the following:
(i) Displacement during the time intervals.
(a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec
(ii) Accelerations at
(a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec.
(iii) Average acceleration
(a) between t = 0 to t = 4 sec.
(b) between t = 0 to t = 7 sec.
(iv) Average velocity during the motion.
View Solution
