Two capacitors of capacitance C and nC are connected in parallel. A battery of emf V is connected across the combination. Now the battery is removed and a dielectric constant K is inserted filling the space between the plates of capacitor of capacitance C. The final potential difference across the system is
n+kn+1
n+1n+k
n−1n+KV
n+1n−kV
The correct Answer is:B
To solve the problem step by step, we will analyze the situation involving two capacitors connected in parallel and the effect of inserting a dielectric into one of them after disconnecting the battery.
Step 1: Understand the Initial Setup
We have two capacitors:
- Capacitor 1: Capacitance C
- Capacitor 2: Capacitance nC
These capacitors are connected in parallel to a battery with an emf V.
Step 2: Calculate the Total Charge Before Removing the Battery
When the battery is connected, the total charge Q stored in the capacitors can be calculated using the formula:
Q=Ceq⋅V
where Ceq is the equivalent capacitance of the capacitors in parallel. The equivalent capacitance for capacitors in parallel is given by:
Ceq=C+nC=(1+n)C
Thus, the total charge Q is:
Q=(1+n)C⋅V
Step 3: Remove the Battery
After the battery is removed, the total charge Q remains the same, but the capacitors are now isolated.
Step 4: Insert the Dielectric
Now, a dielectric with a dielectric constant K is inserted into the capacitor with capacitance C. The capacitance of this capacitor becomes:
C′=K⋅C
The capacitance of the second capacitor remains nC.
Step 5: Calculate the New Equivalent Capacitance
The new equivalent capacitance C′eq of the system after inserting the dielectric is:
C′eq=C′+nC=K⋅C+nC=(K+n)C
Step 6: Calculate the Final Potential Difference
The final potential difference V′ across the capacitors can be calculated using the charge Q and the new equivalent capacitance C′eq:
V′=QC′eq
Substituting the values:
V′=(1+n)C⋅V(K+n)C
The C cancels out:
V′=(1+n)V(K+n)
Final Answer
Thus, the final potential difference across the system is:
V′=V⋅(1+n)(K+n)
We have two capacitors:
- Capacitor 1: Capacitance C
- Capacitor 2: Capacitance nC
When the battery is connected, the total charge Q stored in the capacitors can be calculated using the formula:
Q=Ceq⋅V
where Ceq is the equivalent capacitance of the capacitors in parallel. The equivalent capacitance for capacitors in parallel is given by:
Ceq=C+nC=(1+n)C
Thus, the total charge Q is:
Q=(1+n)C⋅V
After the battery is removed, the total charge Q remains the same, but the capacitors are now isolated.
Now, a dielectric with a dielectric constant K is inserted into the capacitor with capacitance C. The capacitance of this capacitor becomes:
C′=K⋅C
The capacitance of the second capacitor remains nC.
The new equivalent capacitance C′eq of the system after inserting the dielectric is:
C′eq=C′+nC=K⋅C+nC=(K+n)C
The final potential difference V′ across the capacitors can be calculated using the charge Q and the new equivalent capacitance C′eq:
V′=QC′eq
Substituting the values:
V′=(1+n)C⋅V(K+n)C
The C cancels out:
V′=(1+n)V(K+n)
Thus, the final potential difference across the system is:
V′=V⋅(1+n)(K+n)
Topper's Solved these Questions
Similar Questions
The parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View SolutionIn the arrangement shown, the battery is disconnected and a dielectric slab of dielectric constant K is insereted between the plates of capacitor with capacitance C, so as to completely fill the space. What is the final potential differnece across capacitor with capacitance 2C ?
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
View SolutionTwo identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
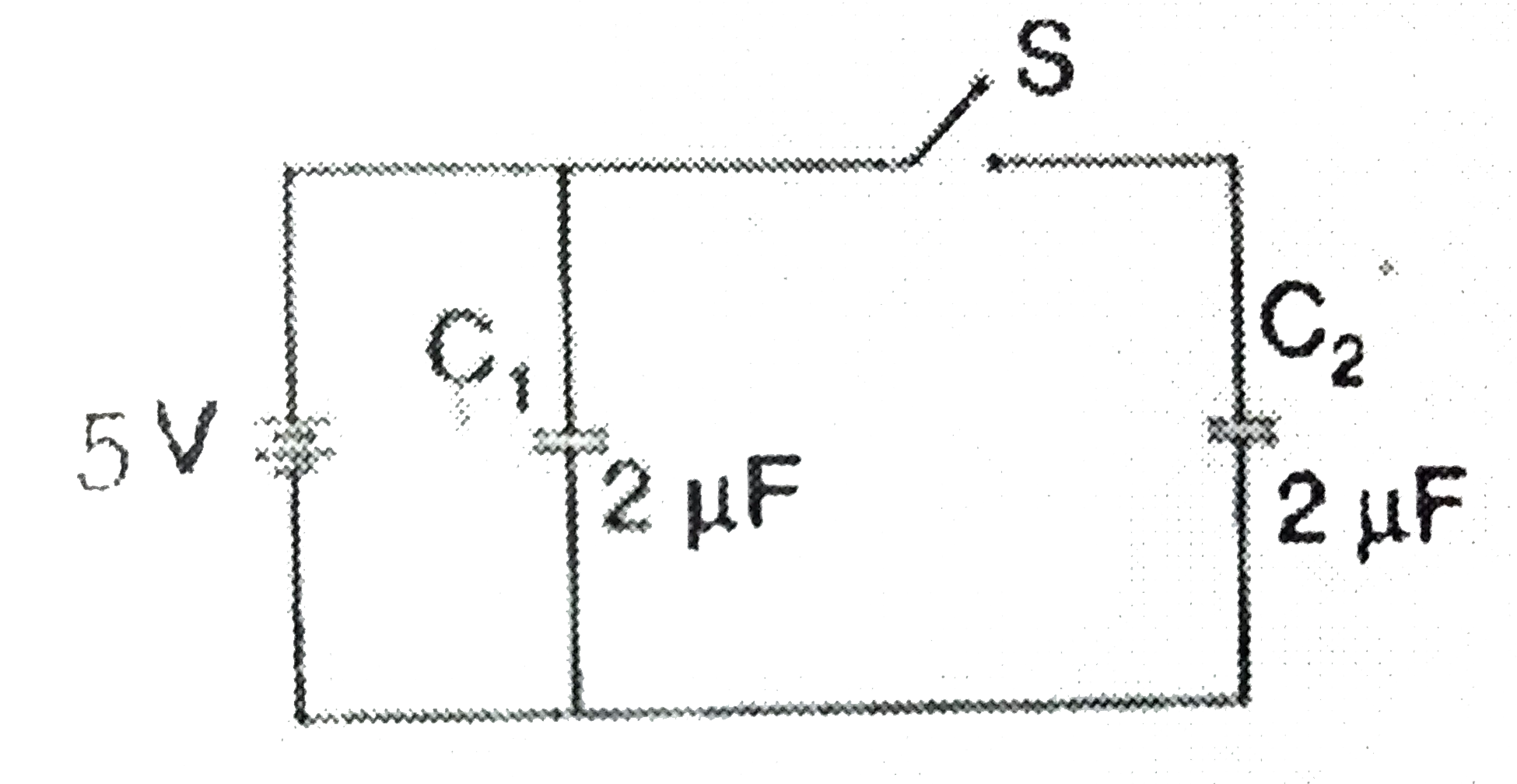
View SolutionFigure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?
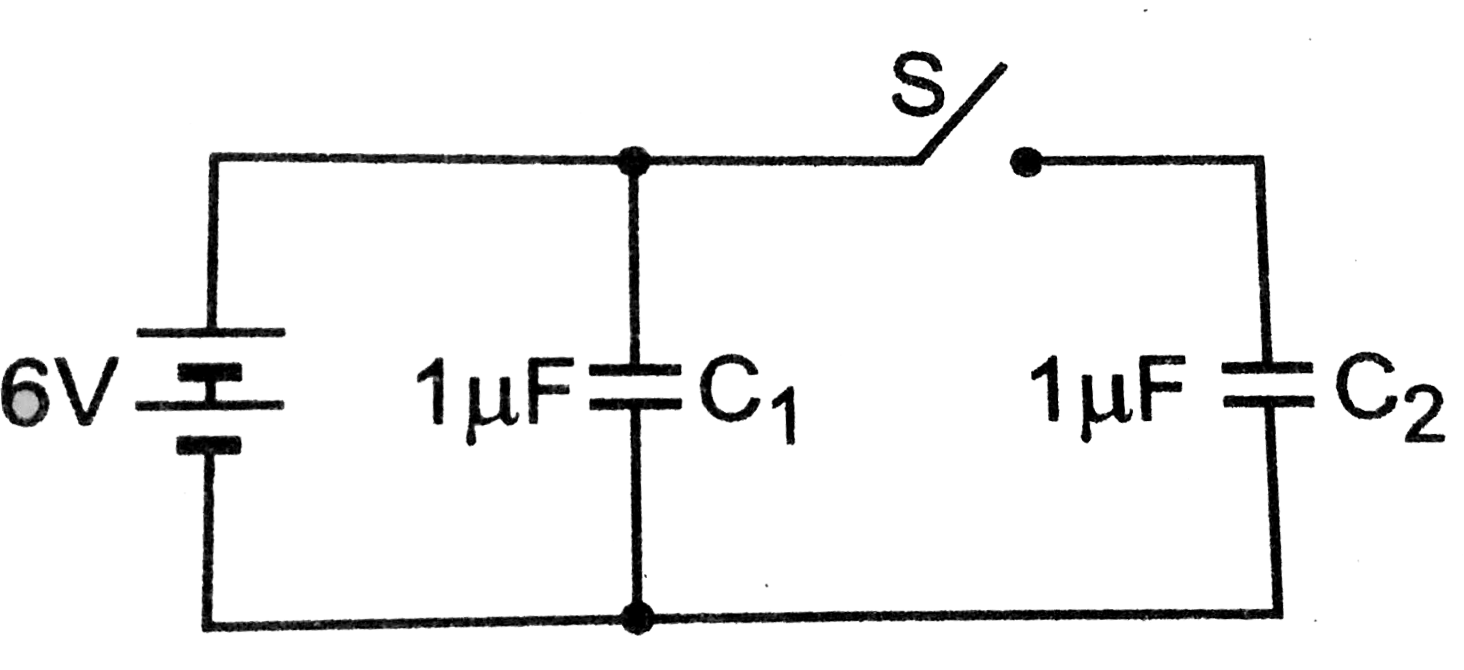
View SolutionFig, shows two indentical capacitors C1andC2 each of 1uF capacitance connected to a battery of 6V. Initially, swich S is closed. After some time, the swich S is left open and dielectric slabs of K = 3 are inserted to filll completely the space between the plates of two capacitors . How will (i) the charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted ?
View SolutionAn air-cored parallel plate capacitor having a capacitance C is charged by connecting it to a battery. Now, it is disconnected from the battery and a dielectric slab of dielectric constant K is inserted between its plates so as to completely fill the space between the plates. Compare :
(I) Initial and final capacitance
(ii) Initial and final charge.
(iii) Initial and final potential difference.
(iv) Initial an final electric field between the plates.
(v) Initial and final energy stored in the capacitor.
View Solution
