During a process ideal gas expands to compress the spring such that 10kJ energy is stored in the spring and 2kJ heat is released from gas to surrounding find the change in internal energy of gas
12kJ
10kJ
8kJ
6kJ
The correct Answer is:A
Step by step video & image solution for During a process ideal gas expands to compress the spring such that 10kJ energy is stored in the spring and 2kJ heat is released from gas to surrounding find the change in internal energy of gas by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
During compression of a spring the work done is 10 kJ and 2 kJ escaped to the surroundings as heat. The change in internal energy ΔU (in kj) is
View SolutionDuring compression of a spring the work done is 10 kJ and 2 kJ escaped to the surroundings as heat. The change in internal energy, ΔU (in kJ) is _________ .
View SolutionAn ideal gas expand against a constant external pressure at 2.0 atmosphere from 20 litre to 40 litre and absorb 10kJ of energy from surrounding . What is the change in internal energy of the system ?
View Solutionp-V diagram of an ideal gas for a process ABC is as shown in the figure.
(a) Find total heat absorbed or released by the gas during the process ABC.
(b) Change in internal energy of the gas during the process ABC.
(c) Plot pressure versus density graph of the gas for the process ABC.
View SolutionWork done by a gas in a given process is −20J. Heat given to the gas is 60J. Find change in internal energy of the gas.
View SolutionWhat happens to the change in internal energy of a gas during adiabatic expansion?
View Solution500cm3 of a sample of an ideal gas is compressed by an average pressure of 0.1atm of 250cm3. During this process, 10J of heat flows out to the surroundings. Calculate the change in internal enegry of the system.
View Solution500cm3 of a sample of an ideal gas is compressed by an average pressure of 0.1atm of 250cm3. During this process, 10J of heat flows out to the surroundings. Calculate the change in internal enegry of the system.
View SolutionA gas is taken along the path AB as shown in fig, if 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.
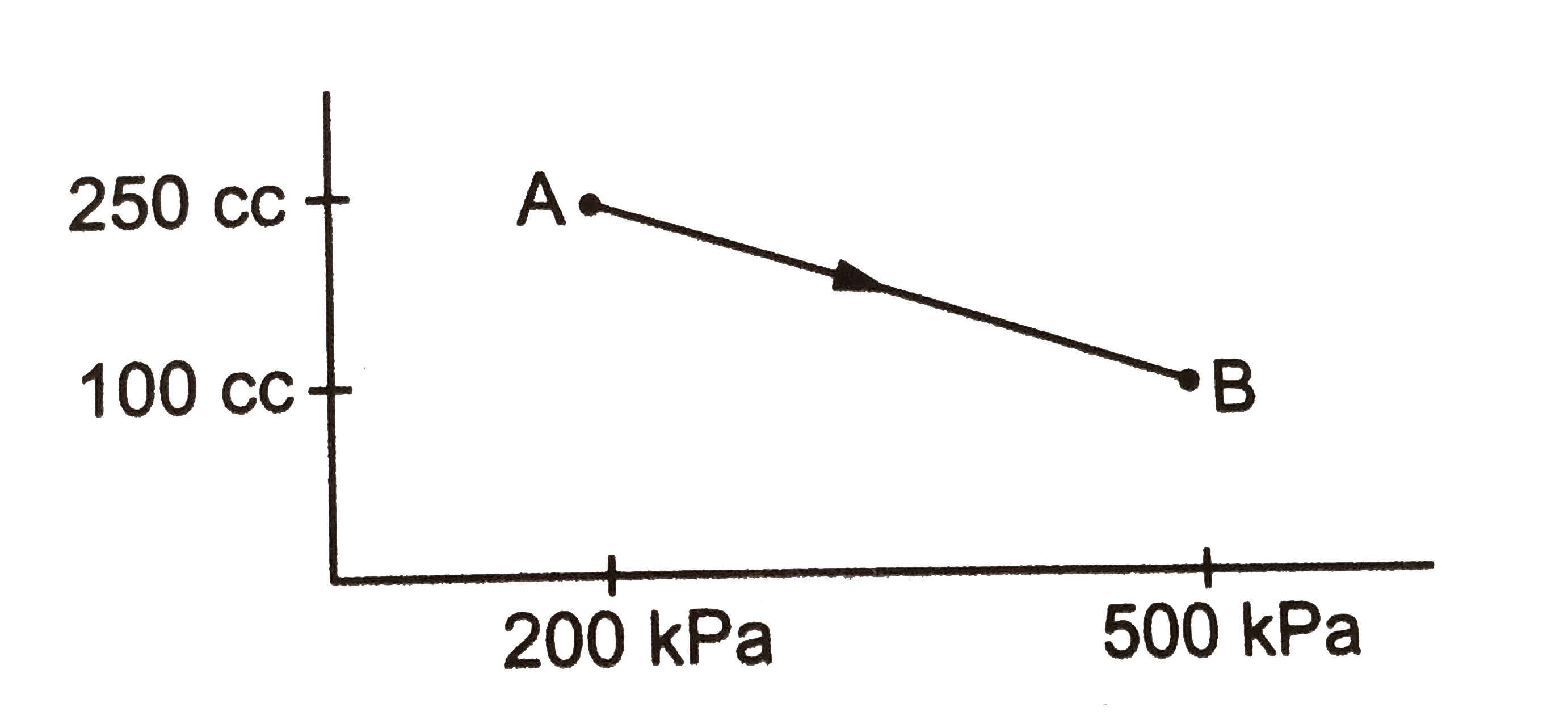
View Solution400 J of work is done on a gas to reduce its volume by compression adiabatically. What is the change in internal energy of the gas?
View Solution