If in a conductor number density of electrons is average relaxation time 25 femtosecond mass of electron being kg, the resistivity would be of the order.
The correct Answer is:D
To find the resistivity of the conductor, we will follow these steps:
Step 1: Understand the relationship between resistivity and conductivity
Resistivity (ρ) is related to conductivity (σ) by the formula:
ρ=1σ
Step 2: Calculate the conductivity (σ)
The conductivity can be calculated using the formula:
σ=ne2τm
where:
- n = number density of electrons
- e = charge of an electron
- τ = average relaxation time
- m = mass of an electron
Step 3: Substitute the given values
Given:
- n=8.5×1028m−3
- e=1.6×10−19C
- τ=25femtoseconds=25×10−15s
- m=9.1×10−31kg
Substituting these values into the conductivity formula:
σ=(8.5×1028)×(1.6×10−19)2×(25×10−15)(9.1×10−31)
Step 4: Calculate e2
First, calculate e2:
e2=(1.6×10−19)2=2.56×10−38C2
Step 5: Substitute e2 into the conductivity formula
Now substitute e2 back into the conductivity formula:
σ=(8.5×1028)×(2.56×10−38)×(25×10−15)(9.1×10−31)
Step 6: Calculate the fraction
Calculate the fraction:
(25×10−15)(9.1×10−31)≈2.747×1015
Step 7: Substitute and calculate σ
Now substitute this back into the conductivity equation:
σ≈(8.5×1028)×(2.56×10−38)×(2.747×1015)
Calculating this gives:
σ≈5.87×10−6S/m
Step 8: Calculate resistivity (ρ)
Now, using the relationship ρ=1σ:
ρ≈15.87×10−6≈1.70×105Ω⋅m
Step 9: Convert to appropriate order
Since we are looking for the order of resistivity, we can express it as:
ρ≈1.7×10−8Ω⋅m
Thus, the resistivity would be of the order 10−8Ω⋅m.
Final Answer
The resistivity is approximately 10−8Ω⋅m.
---
Resistivity (ρ) is related to conductivity (σ) by the formula:
ρ=1σ
The conductivity can be calculated using the formula:
σ=ne2τm
where:
- n = number density of electrons
- e = charge of an electron
- τ = average relaxation time
- m = mass of an electron
Given:
- n=8.5×1028m−3
- e=1.6×10−19C
- τ=25femtoseconds=25×10−15s
- m=9.1×10−31kg
σ=(8.5×1028)×(1.6×10−19)2×(25×10−15)(9.1×10−31)
First, calculate e2:
e2=(1.6×10−19)2=2.56×10−38C2
Now substitute e2 back into the conductivity formula:
σ=(8.5×1028)×(2.56×10−38)×(25×10−15)(9.1×10−31)
Calculate the fraction:
(25×10−15)(9.1×10−31)≈2.747×1015
Now substitute this back into the conductivity equation:
σ≈(8.5×1028)×(2.56×10−38)×(2.747×1015)
Calculating this gives:
σ≈5.87×10−6S/m
Now, using the relationship ρ=1σ:
ρ≈15.87×10−6≈1.70×105Ω⋅m
Since we are looking for the order of resistivity, we can express it as:
ρ≈1.7×10−8Ω⋅m
The resistivity is approximately 10−8Ω⋅m.
Topper's Solved these Questions
Similar Questions
In conductor, if the number of conduction electrons per unit volume is 8.5×1028m−3 and mean free time is 25 fs (femto seconds), it's approximate resistivity is : (me=9.1×10−31kg)
View SolutionThe kinetic energy of an electron is 4.55×10−25J .The mass of electron is 9.1×10−34kg. Calculate velocity of the electron.
View SolutionIf n ,e,m and τ are free electron density in conductor , charge of electron, mass of electron and relaxation time of free electrons , then resistivity ρ of the conductor can be expressed as
View SolutionThe kinetic energy of an electron is 4.55×10−25 J. Calculate the wavelength, (h=6.6×10−34 Jsec,mass of electron=9.1×10−31 kg).
View SolutionFind the relaxation time for free electrons in copper, if the density of mobile electrons in copper, if the density of mobile electrons is 8.4×1028m−3. The resistivity of copper at room temperature is 1.7×10−8Ωm.
Given : mass of electron =9.11×10−31kg and charge on electron =1.6×10−19C.
View SolutionWhen 5 V potential difference is applied across a wire of length 0.1 m, the drift speed of electrons is 2.5×10−4ms−1. If the electron density in the wire is 8×1028m−3, the resistivity of the material is close to :
View SolutionThe mass of half mole of electrons is about (Given: Mass of electron =9.1×10−28 g)
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
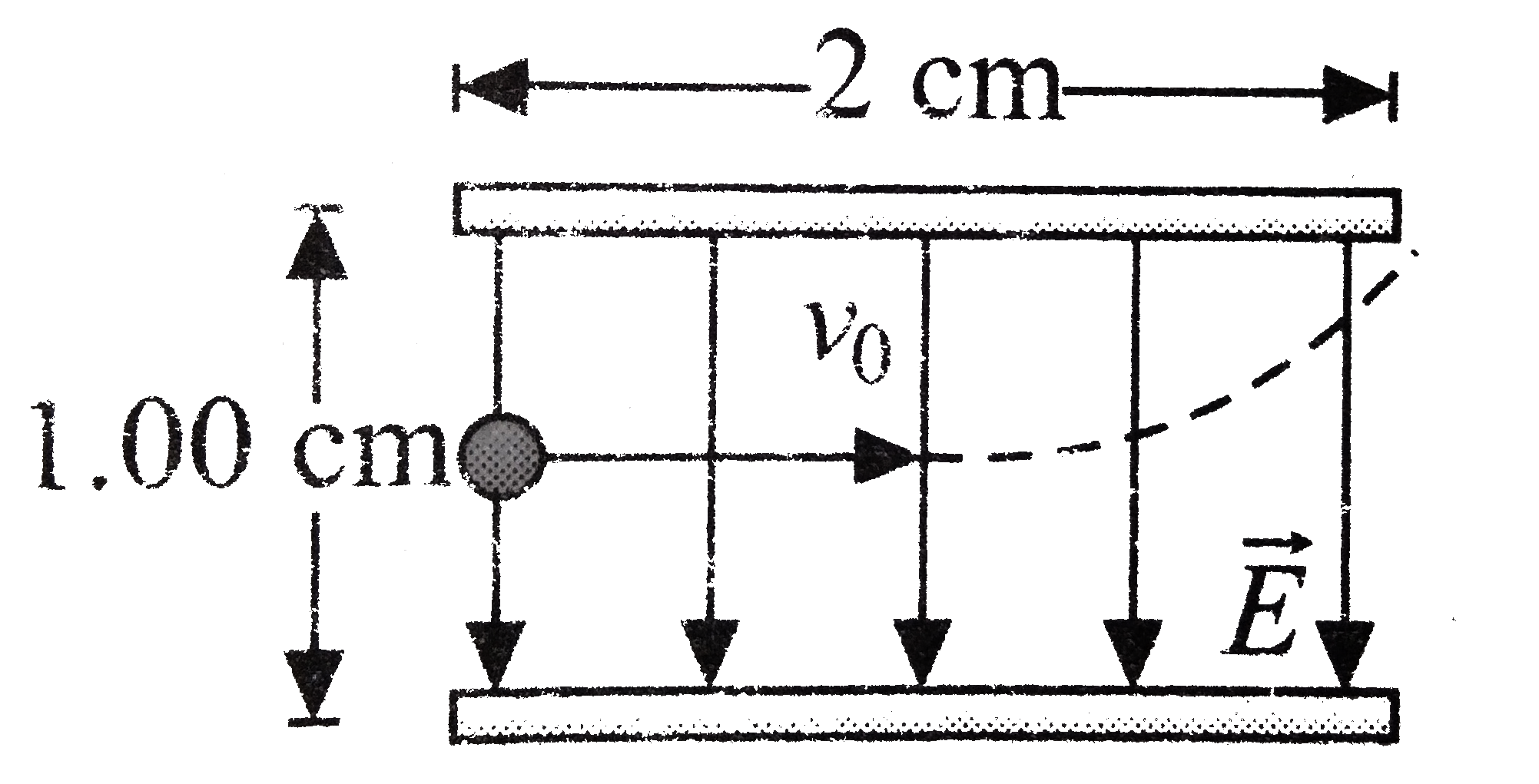
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionDetermine the de Broglie wavelength of a proton, whose kinetice energy is equal to the rest of the mass energy of an electron. Given that the mass of an electron is 9×10−31 kg and the mass of a proton is 1837 times as that of the electron.
View Solution
