A stationary source of sound is emitting sound of frequency 500Hz. Two observers A and B lying on the same line as the source, observe frequencies 480Hz and 530Hz respectively. The velocity of A and B respectively are (in m/s), speed of sound =300m/s.
12,18
8,18
18,8
18,12
The correct Answer is:A
To solve the problem, we will use the Doppler effect formula for sound. The frequency observed by an observer moving relative to a stationary source can be calculated using the following formula:
f′=v+vovf
Where:
- f′ is the observed frequency,
- v is the speed of sound,
- vo is the velocity of the observer (positive if moving towards the source, negative if moving away),
- f is the frequency of the source.
Step 1: Calculate the velocity of observer A
Given:
- Frequency of source, f=500Hz
- Observed frequency by A, fA=480Hz
- Speed of sound, v=300m/s
Since observer A is moving away from the source, we will take vo as negative.
Using the formula:
fA=v−vAvf
Substituting the known values:
480=300−vA300×500
Step 2: Rearranging the equation
Multiply both sides by 300:
480×300=(300−vA)×500
Now calculate 480×300:
144000=(300−vA)×500
Step 3: Solve for 300−vA
Divide both sides by 500:
144000500=300−vA
288=300−vA
Step 4: Isolate vA
Rearranging gives:
vA=300−288=12m/s
Step 5: Calculate the velocity of observer B
Now, for observer B who is moving towards the source, we will take vo as positive.
Using the formula:
fB=v+vBvf
Substituting the known values:
530=300+vB300×500
Step 6: Rearranging the equation for B
Multiply both sides by 300:
530×300=(300+vB)×500
Calculating 530×300:
159000=(300+vB)×500
Step 7: Solve for 300+vB
Divide both sides by 500:
159000500=300+vB
318=300+vB
Step 8: Isolate vB
Rearranging gives:
vB=318−300=18m/s
Final Answer
The velocities of observers A and B are:
- vA=12m/s
- vB=18m/s
- f′ is the observed frequency,
- v is the speed of sound,
- vo is the velocity of the observer (positive if moving towards the source, negative if moving away),
- f is the frequency of the source.
- Frequency of source, f=500Hz
- Observed frequency by A, fA=480Hz
- Speed of sound, v=300m/s
fA=v−vAvf
480=300−vA300×500
480×300=(300−vA)×500
144000=(300−vA)×500
144000500=300−vA
288=300−vA
vA=300−288=12m/s
fB=v+vBvf
530=300+vB300×500
530×300=(300+vB)×500
159000=(300+vB)×500
159000500=300+vB
318=300+vB
vB=318−300=18m/s
- vA=12m/s
- vB=18m/s
Topper's Solved these Questions
Similar Questions
A stationary source emits sound waves of frequency 500 Hz. Two observes moving along a line passing through the source detect sount to be of frequencies 480 Hz and 530 Hz.Their respective speeds are, in ms−1
(Given speed of sound =300m/s)
View SolutionA source emits a sound of frequency of 400 Hz , but the listener hears it to be 390 Hz . Then
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
View SolutionA source frequency f gives 5 beats when sounded with a frequency 200Hz. The second harmonic of same source gives 10 beats when sounded with a source of frequency 420Hz. The value of f is
View SolutionA source frequency f gives 5 beats when sounded with a frequency 200Hz. The second harmonic of same source gives 10 beats when sounded with a source of frequency 420Hz. The value of f is
View SolutionAn observer moves on the same line on which two sources of sound of frequency 660Hz are present. The observer observes beat frequency of 10Hz. If speed of sound is 300m/s then speed of the observer is:
View Solution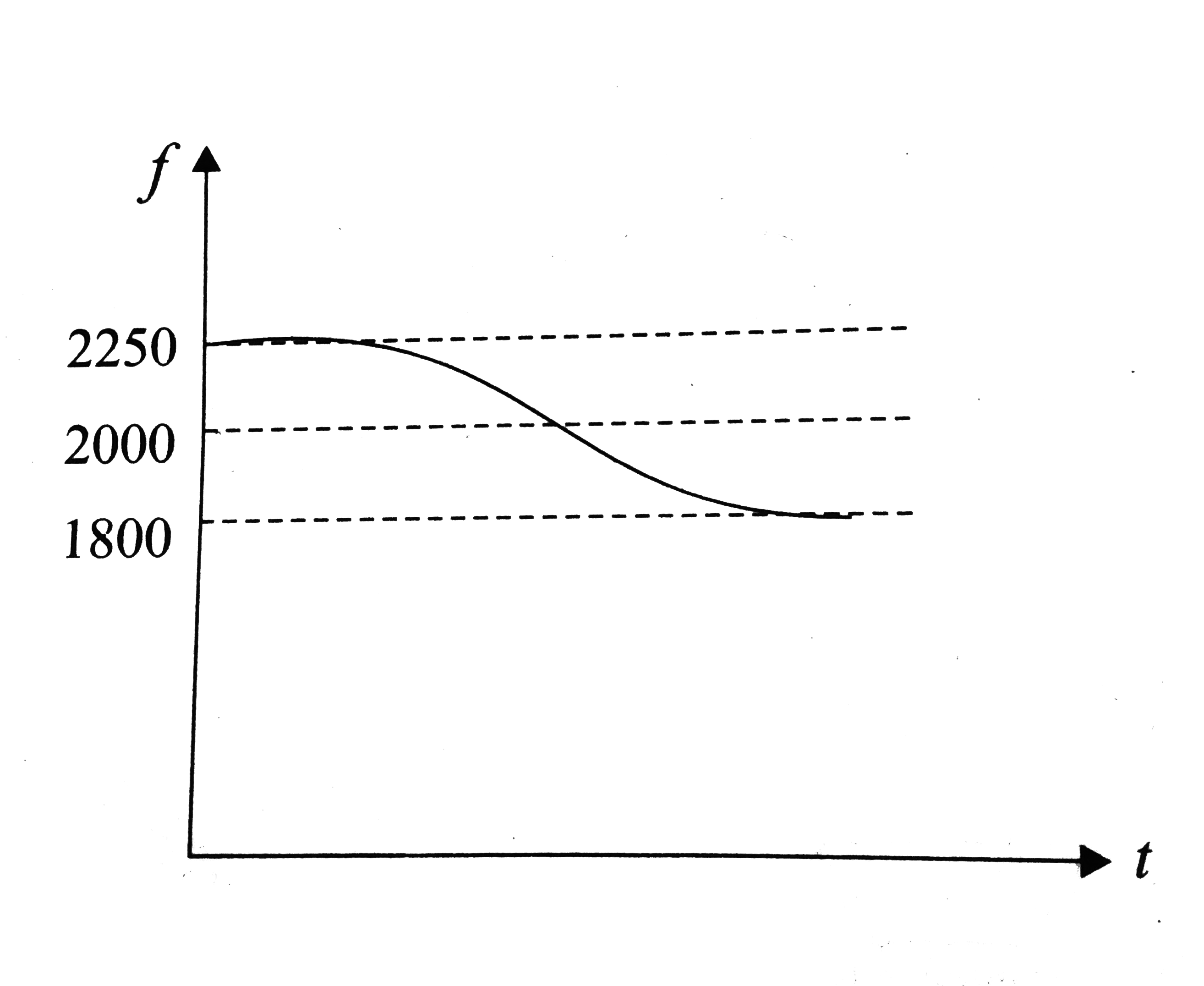
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionA source of sound emitting a note of frequency 200 Hz moves towards an observer with a velocity v equal to the velocity of sound. If the observer also moves away from the source with the same velocity v, the apparent frequency heard by the observer is
View SolutionA siren emitting sound of frequency 800Hz is going away from a static listener with a speed of 30 m/s. Frequency of the sound to be heard by the listener is ( Take velocity of sound as 300 m/s )
View SolutionA source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, A away from the wall and B towards the wall and Inside the source, Velocity of sound in air is 330 m/s.

Find the frequency of reflected sound observed by observer B
View Solution
