Pressure of 1 mole ideal is given by
P=P0[1−12(V0V)2] V0 to 2V0. Find change in temperature.
5P0V04R
P0V4R
3P0V4R
P0V2R
The correct Answer is:A
To solve the problem, we need to find the change in temperature of 1 mole of an ideal gas when its volume changes from V0 to 2V0. The pressure of the gas is given by:
P=P0(1−12(V0V)2)
Step 1: Use the Ideal Gas Law
We start with the ideal gas equation:
PV=nRT
For 1 mole of gas, n=1. Thus, we can write:
P=RTV
Step 2: Substitute Pressure in Terms of Temperature
We can substitute the expression for pressure P from the given equation into the ideal gas law:
RTV=P0(1−12(V0V)2)
Step 3: Rearranging the Equation
Now, we can rearrange this equation to express T in terms of V:
RT=P0V(1−12(V0V)2)
Dividing both sides by R:
T=P0VR(1−12(V0V)2)
Step 4: Calculate Temperature at Initial Volume V0
Now, we calculate the temperature T1 when V=V0:
T1=P0V0R(1−12(V0V0)2)
This simplifies to:
T1=P0V0R(1−12)=P0V0R⋅12=P0V02R
Step 5: Calculate Temperature at Final Volume 2V0
Next, we calculate the temperature T2 when V=2V0:
T2=P0(2V0)R(1−12(V02V0)2)
This simplifies to:
T2=P0(2V0)R(1−12⋅14)=P0(2V0)R(1−18)=P0(2V0)R⋅78
Thus,
T2=7P0V04R
Step 6: Find the Change in Temperature
Now, we find the change in temperature ΔT:
ΔT=T2−T1=7P0V04R−P0V02R
To combine these fractions, we convert P0V02R to have a common denominator:
ΔT=7P0V04R−2P0V04R=(7−2)P0V04R=5P0V04R
Final Answer
Thus, the change in temperature is:
ΔT=5P0V04R
We start with the ideal gas equation:
We can substitute the expression for pressure P from the given equation into the ideal gas law:
Now, we can rearrange this equation to express T in terms of V:
Now, we calculate the temperature T1 when V=V0:
Next, we calculate the temperature T2 when V=2V0:
Now, we find the change in temperature ΔT:
Thus, the change in temperature is:
Topper's Solved these Questions
Similar Questions
Pressure of 1 mole ideal gas is given by
P=P0[1−12(V0V)2] V to 2V. Find change in temperature.
View SolutionThe internal energy of a gas is given by U=PV2. At constant volume, state of gas changes from (P0,V0) to (3P0,V0) then
View SolutionOne mole of an ideal gas undergoes a process p=p01+(V0V)2. Here, p0 and V0 are constants. Change in temperature of the gas when volume is changed from V=V0 to V=2V0 is
View SolutionOne mole of an ideal gas undergoes a process
p=p01+(VV0)2
where p0and V0 are constants. Find temperature of the gaas when V=V0.
View SolutionVariation of volume with temperature was first studied by French chemist, Jacques Charles, in 1787 and then extended by another French chemist Joseph Gay-Lussac in 1802. For a fixed mass of a gas under isobaric condition, variation of volume V with temperature t°C is given by V = V0[l+αt] where V0 is the volume at 0°C, at constant pressure.
1 or every 1° change in temperature, the volume of the gas changes by............... of the volume at 0∘ C
View SolutionIf n moles of an ideal gas undergoes a thermodynamic process P=P0[1+(2V0V)2]−1, then change in temperature of the gas when volume is changed from V=V0 to V=2V0 is [Assume P0 and V0 are constants]
View SolutionOne mole of an ideal gas passes through a process where pressure and volume obey the relation P=P0[1−12(V0V)2] Here P0 and V0 are constants. Calculate the change in the temperature of the gas if its volume changes from V0 to 2V0.
View SolutionIn process T∝1V, pressure of the gas increases from p0 to 4p0. Match the following.
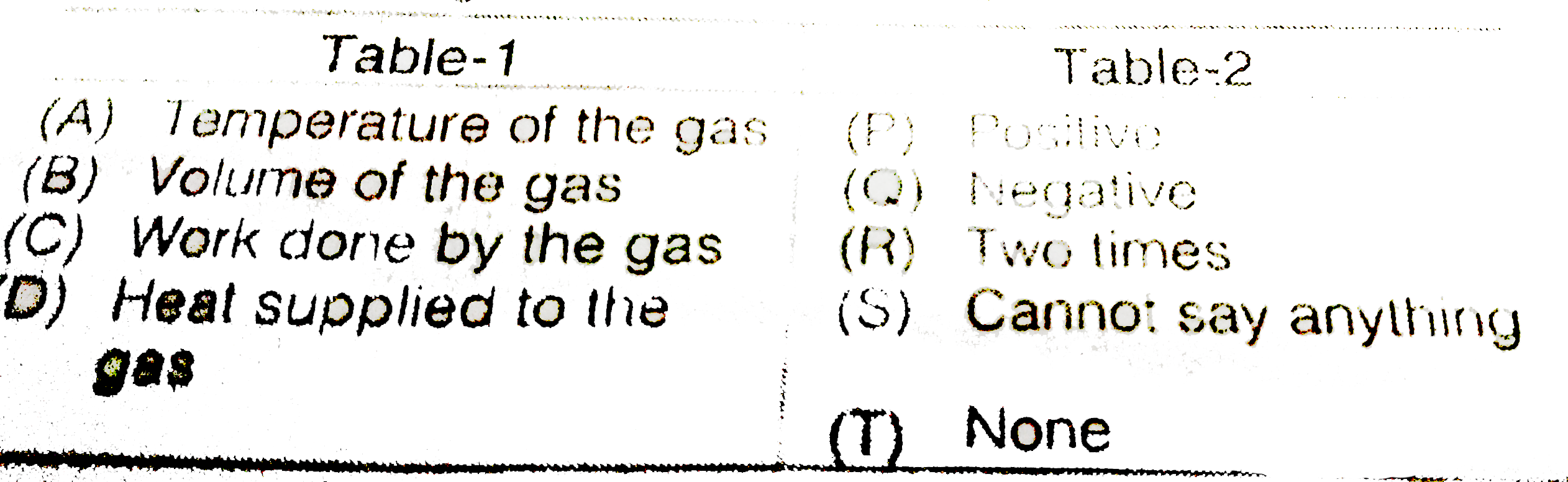
View SolutionOne mole of ideal gas goes through processP=2V21+V2. Then change in temperature of gas when volume changes from V=1m2 to 2m2 is :
View SolutionDraw the P-T and V-T diagrams of an isochoric process of n moles an ideal gas from pressure P0 volume V0 to pressure 4P0, indicating the pressures and temperatures of the gas in the initial and the final states.
View Solution
