A solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
200
140
120
180
The correct Answer is:B
To solve the problem, we need to find the ratio of the moments of inertia I1I2 for a disc and a solid sphere, respectively.
1. Identify the Masses and Shapes:
- We have a solid sphere of mass m and radius R.
- The sphere is divided into two parts:
- Part 1: Mass 7m8 converted into a disc of radius 2R.
- Part 2: Mass m8 converted into a solid sphere of radius r.
2. Calculate the Moment of Inertia of the Disc I1:
- The formula for the moment of inertia of a disc about its central axis is given by:
I1=12MR2
- Here, M=7m8 and R=2R.
- Substituting these values:
I1=12(7m8)(2R)2=12(7m8)(4R2)=7m4
3. Calculate the Moment of Inertia of the Solid Sphere I2:
- The formula for the moment of inertia of a solid sphere about its central axis is:
I2=25mR2
- Here, the mass is m8 and we need to find the radius r.
- To find r, we use the fact that the densities of both spheres are equal:
mV=m843πr3
- Setting the densities equal:
m43πR3=m843πr3
- This simplifies to:
R3=r38⟹r3=8R3⟹r=R2
- Now substituting r back into the moment of inertia formula:
I2=25(m8)(R2)2=25(m8)(R24)=mR280
4. Calculate the Ratio I1I2:
- Now we can find the ratio:
I1I2=7m4mR280=7m4⋅80mR2=7⋅804R2=5604R2=140R2
5. Final Result:
- The final answer is:
I1I2=140
- We have a solid sphere of mass m and radius R.
- The sphere is divided into two parts:
- Part 1: Mass 7m8 converted into a disc of radius 2R.
- Part 2: Mass m8 converted into a solid sphere of radius r.
- The formula for the moment of inertia of a disc about its central axis is given by:
I1=12MR2
- Here, M=7m8 and R=2R.
- Substituting these values:
I1=12(7m8)(2R)2=12(7m8)(4R2)=7m4
- The formula for the moment of inertia of a solid sphere about its central axis is:
I2=25mR2
- Here, the mass is m8 and we need to find the radius r.
- To find r, we use the fact that the densities of both spheres are equal:
mV=m843πr3
- Setting the densities equal:
m43πR3=m843πr3
- This simplifies to:
R3=r38⟹r3=8R3⟹r=R2
- Now substituting r back into the moment of inertia formula:
I2=25(m8)(R2)2=25(m8)(R24)=mR280
- Now we can find the ratio:
I1I2=7m4mR280=7m4⋅80mR2=7⋅804R2=5604R2=140R2
- The final answer is:
I1I2=140
Topper's Solved these Questions
Similar Questions
The magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M, respectively. Find the ratio of (I1)/(I2)) if r1>R and r2>R.
View SolutionA solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.

View SolutionThe moment of ineria (I) of a sphere of radius R and mass M is given by
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
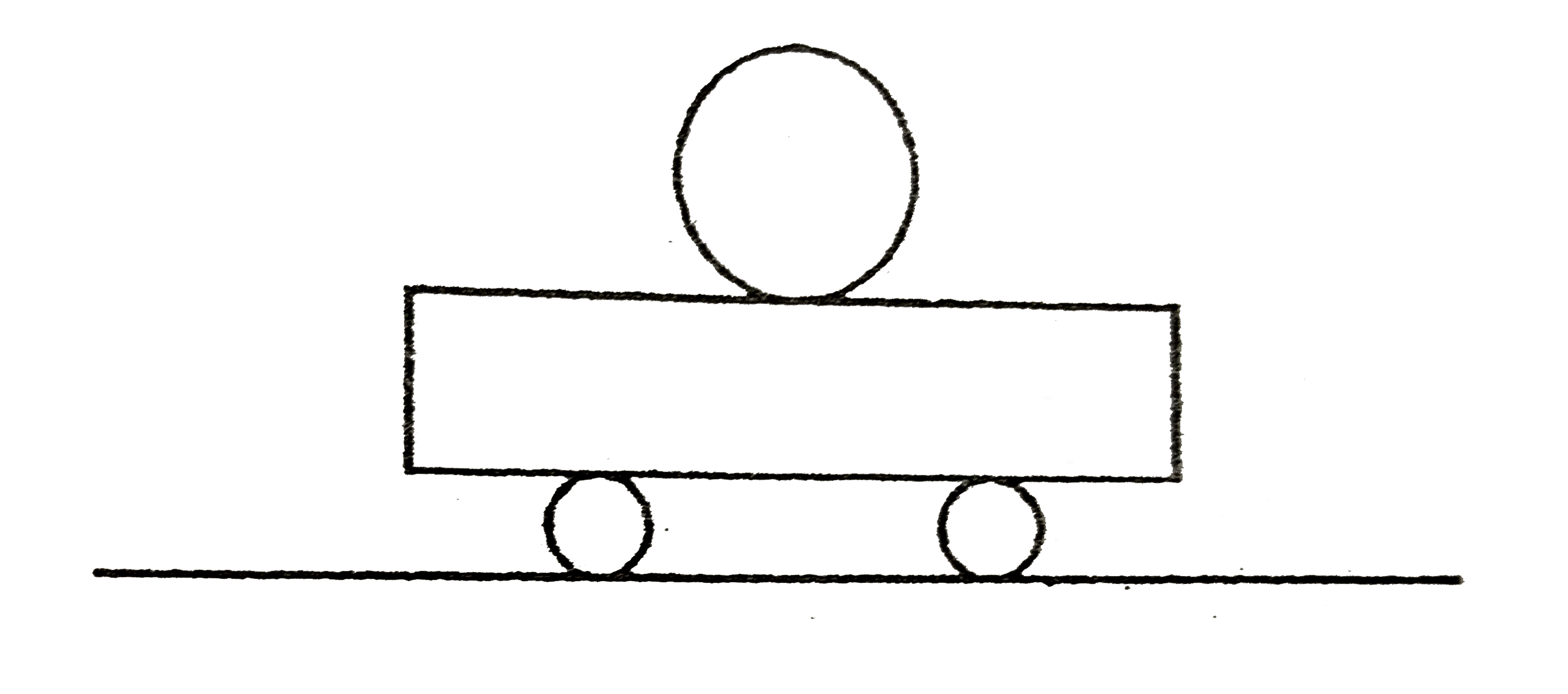
Acceleration of centre of mass of sphere is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
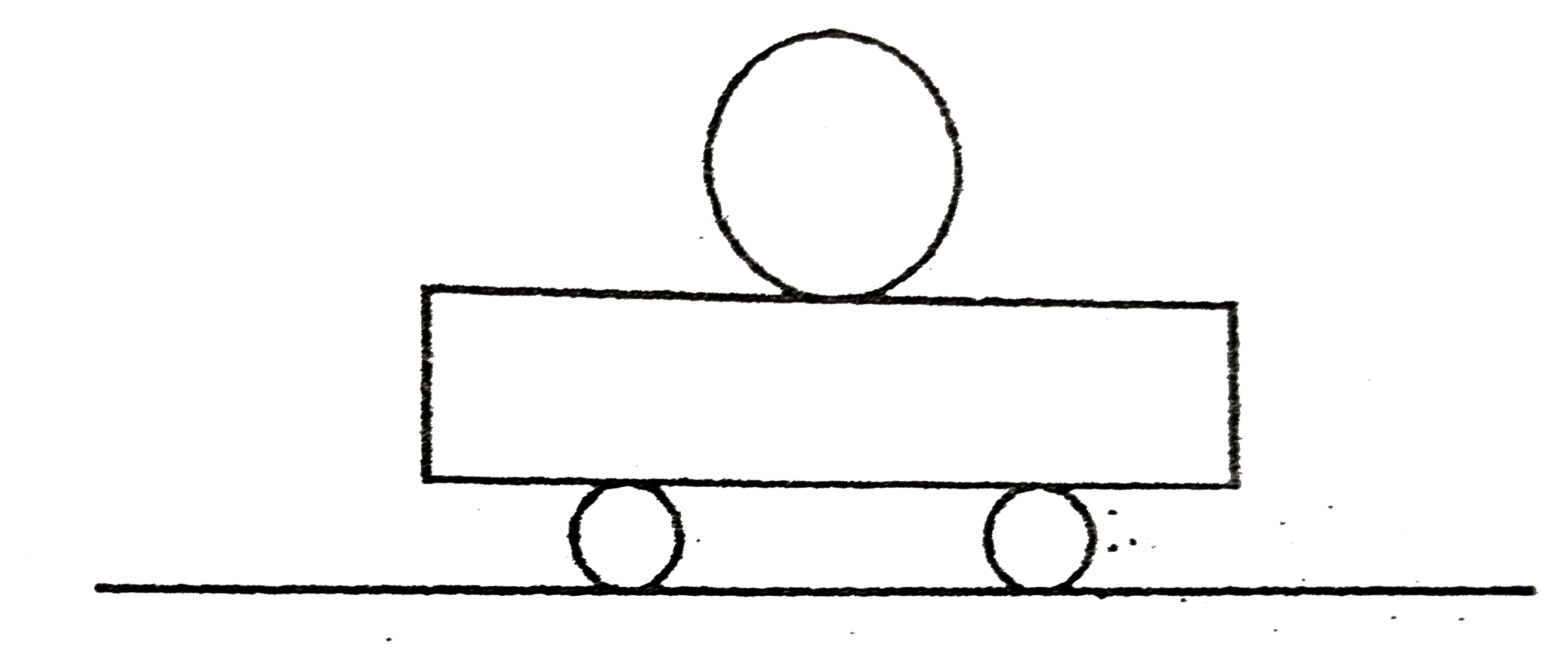
Angular acceleration of sphere is
View SolutionPercentage error in measuring the radius and mass of a solid sphere are 3 % & 1 % respectively. The error in measurement of moment of inertia about to its diameter is :-
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping. Force of friction between sphere and plank is

View Solution
