A boy's catapult is made of rubber cord which is 42cm long, with 6mm diameter of cross-section and of negligible mass. The boy keeps a stone weighing 0.02kg on it and stretches the cond by 20cm by applying a constant force. When released. The stone flies off with a velocity of 20ms−1. Neglect the change in the area of cross-section of the cord while stretched. The Young's modulus of rubber is closet to:
106Nm−2
104Nm−2
108Nm−2
103Nm−2
The correct Answer is:A
To find the Young's modulus of the rubber cord used in the catapult, we can follow these steps:
1. Identify the Given Values:
- Length of the rubber cord (L) = 42 cm = 0.42 m
- Diameter of the rubber cord (D) = 6 mm = 0.006 m
- Radius of the rubber cord (r) = D/2 = 0.003 m
- Mass of the stone (m) = 0.02 kg
- Stretching of the cord (ΔL) = 20 cm = 0.20 m
- Final velocity of the stone (v) = 20 m/s
2. Calculate the Cross-Sectional Area (A):
The cross-sectional area of the rubber cord can be calculated using the formula for the area of a circle:
A=πr2=π(0.003)2=π(9×10−6)≈2.827×10−5m2
3. Calculate the Strain (ε):
Strain is defined as the change in length divided by the original length:
Strain(ϵ)=ΔLL=0.200.42≈0.4762
4. Calculate the Stress (σ):
Stress is defined as the force applied per unit area. The force (F) exerted by the stone can be calculated using its weight:
F=mg=0.02×9.81≈0.1962N
Then, stress can be calculated as:
Stress(σ)=FA=0.19622.827×10−5≈6947.5N/m2
5. Relate Young's Modulus (Y) to Stress and Strain:
Young's modulus is defined as the ratio of stress to strain:
Y=σϵ=6947.50.4762≈14580.5N/m2
6. Equate Energy:
The elastic potential energy stored in the stretched rubber cord is equal to the kinetic energy of the stone when it is released:
12mv2=12Yϵ2AL
Rearranging gives:
Y=mv2ϵ2AL
7. Substituting Values:
Y=0.02×(20)2(0.4762)2×(2.827×10−5)×0.42
Calculate the above expression to find Y.
8. Final Calculation:
After substituting the values and simplifying, we find:
Y≈3×106N/m2
Conclusion:
The Young's modulus of the rubber is approximately 3×106N/m2.
- Length of the rubber cord (L) = 42 cm = 0.42 m
- Diameter of the rubber cord (D) = 6 mm = 0.006 m
- Radius of the rubber cord (r) = D/2 = 0.003 m
- Mass of the stone (m) = 0.02 kg
- Stretching of the cord (ΔL) = 20 cm = 0.20 m
- Final velocity of the stone (v) = 20 m/s
The cross-sectional area of the rubber cord can be calculated using the formula for the area of a circle:
A=πr2=π(0.003)2=π(9×10−6)≈2.827×10−5m2
Strain is defined as the change in length divided by the original length:
Strain(ϵ)=ΔLL=0.200.42≈0.4762
Stress is defined as the force applied per unit area. The force (F) exerted by the stone can be calculated using its weight:
F=mg=0.02×9.81≈0.1962N
Then, stress can be calculated as:
Stress(σ)=FA=0.19622.827×10−5≈6947.5N/m2
Young's modulus is defined as the ratio of stress to strain:
Y=σϵ=6947.50.4762≈14580.5N/m2
The elastic potential energy stored in the stretched rubber cord is equal to the kinetic energy of the stone when it is released:
12mv2=12Yϵ2AL
Rearranging gives:
Y=mv2ϵ2AL
Y=0.02×(20)2(0.4762)2×(2.827×10−5)×0.42
Calculate the above expression to find Y.
After substituting the values and simplifying, we find:
Y≈3×106N/m2
The Young's modulus of the rubber is approximately 3×106N/m2.
Topper's Solved these Questions
Similar Questions
The combination of plots which does not represent isothermal expansion of an ideal gas is :
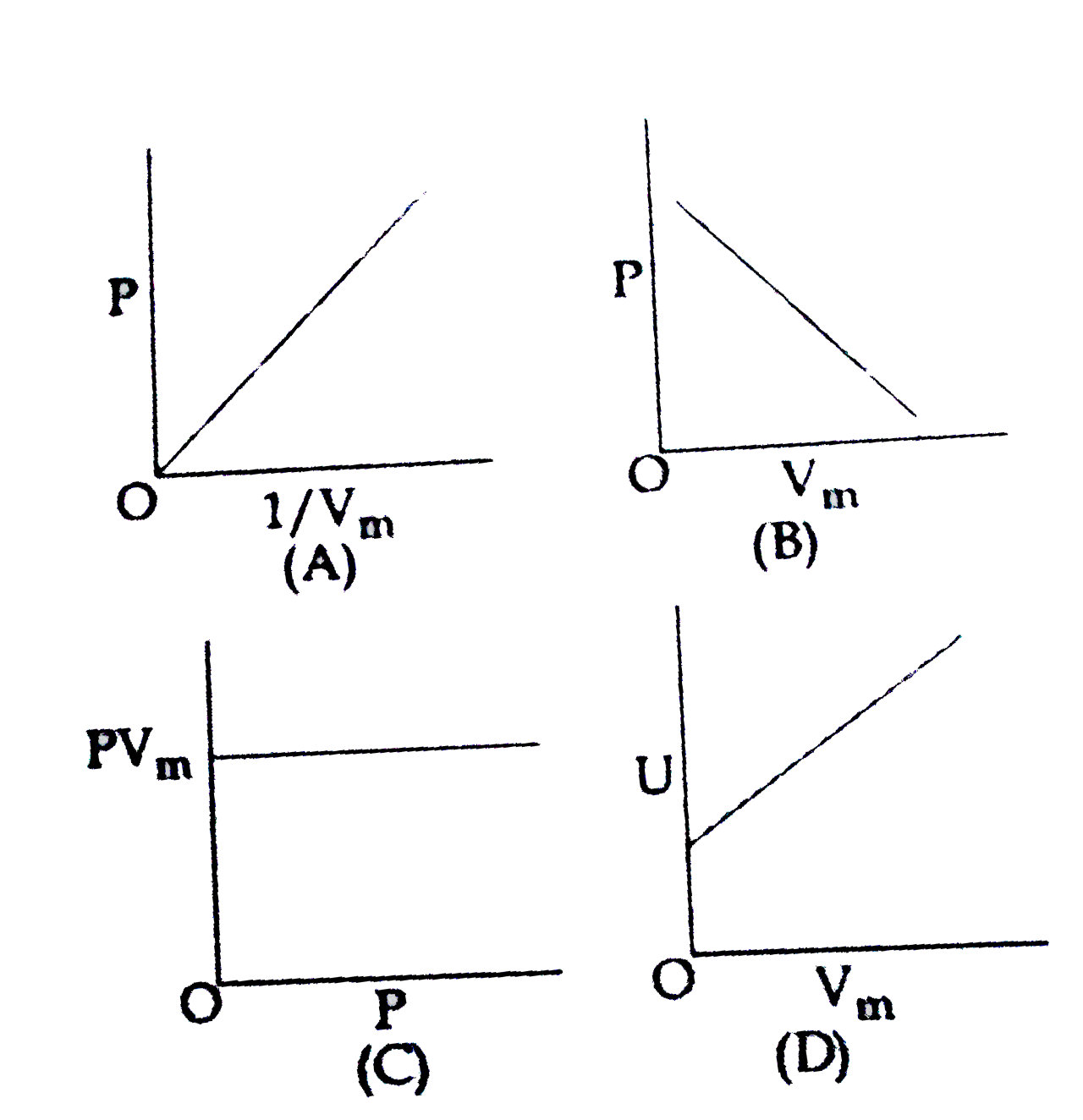
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionA boy has a catapult made of a rubber cord of length 42 cm and diameter 6.0 mm . The boy stretches the cord by 20 cm to catapult a stone of mass 20 g . The stone flies off with a speed of 20 ms^(-1) . Find Young's modulus for rubber. Ignore the change in the cross section of the cord in streching.
View SolutionA catapult consists of two parallel rubber cords each of length 20cm and cross-sectional area 5cm^(2) . When stretched by 8cm , it can throw a stone of mass 4gm to a vertical height 5m , the Young's modulus of elasticity of rubber is [g = 10m//sec^(2)]
View SolutionWhat type of energy is possessed : (a) by the stretched rubber strings of a catapult ? (b) by the piece of stone which is thrown away on releasing the stretched rubber strings of catapult ?
View SolutionA rubber cord of cross-sectional area 2 cm^(2) has a length of 1 m. When a tensile force of 10 N is applied, the length of the cord increases by 1 cm. What is the Young's modulus of rubber ?
View SolutionThe length of a rubber cord doubles, when stretched. Its Young's modulus is equal to
View SolutionA rubber cord of cross sectional area 1mm2 and unstretched length 10cm is stretched to 12cm and then released to project a stone of mass 5 gram.
If Y for rubber =5×108N/m2, then the tension in the rubber cord is
View Solutionएक बालक की गुलेल 42 cm लम्बी और 6mm अनुप्रस्थ-काट के व्यास की रबड़ की डोरी की बनी है, जिसका द्रव्यमान नगण्य है। बालक 0.02 kg भार का एक पत्थर इसपर रखता है और डोरी को एक नियत बल से 20 cm द्वारा तनित करता है। जब इसे छोड़ता है, तब पत्थर 20ms−1 के वेग से जाता है। तानित होने पर डोरी के अनुप्रस्थ-काट में परिवर्तन नगण्य है। रबड़ के यंग प्रत्यास्थता गुणांक का निकटतम मान है
View SolutionA boy stretches the rubber cord of his catapult by 6 cm. IF 0.588 N of force is required for stretching the cord by 1 cm, then calculate the average force acting on the cord of the catapult. With what velocity will a stone of mass 8 g be projected under such condition?
View SolutionAs stone of mass .m. is projected from a rubber catpult of of length .l. and cross-sectional area A stretched by an amount .e.. If Y be the young.s modulus of rubber then find the velocity of projection of stone?
View SolutionThe length of a rubber cord doubles, when stretched. Its Young's modulus is equal to
View SolutionA rubber cord has a cross -sectional area 1mm2and total un-stretched length10.0cm. It is stretched to 12.0cm and then released to project a missile of mass 5.0 g. Taking young's modulus Y for rubber as 5.0×108N/m2.Calculate the velocity of projection .
View SolutionA rubber cord of cross-sectional area 2cm2 has a length of 1m. When a tensile force of 10 N is applied , the length of the coed increases 1 cm. What is the Young's modulus of rubber ?
View Solution