A thermally insulated vessel contains of water at . Then the air from the vessel is pumped out adiabatically. A fraction of water turms into ice and the rest evaporates at itself. The mass of evaporated water will be closest to :
(Latent heat of vaporization of water and Latent heat of Fusion of water )
The correct Answer is:B
To solve the problem, we need to analyze the energy exchanges that occur when air is pumped out of the thermally insulated vessel containing water at 0°C. The process leads to some of the water turning into ice while the rest evaporates, both at 0°C.
1. Identify the Given Data:
- Mass of water (m) = 150 g = 0.150 kg
- Latent heat of fusion of water (L_f) = 3.36×105J/kg
- Latent heat of vaporization of water (L_v) = 2.10×106J/kg
2. Define Variables:
- Let x be the mass of water that turns into ice (in kg).
- The mass of water that evaporates will then be 0.150−x kg.
3. Set Up the Energy Balance Equation:
- The heat lost by the water turning into ice is given by:
Qloss=x⋅Lf
- The heat gained by the water turning into vapor is given by:
Qgain=(0.150−x)⋅Lv
- Since the system is adiabatic, the heat lost by the ice formation equals the heat gained by the vaporization:
x⋅Lf=(0.150−x)⋅Lv
4. Substitute the Values:
x⋅(3.36×105)=(0.150−x)⋅(2.10×106)
5. Expand and Rearrange the Equation:
3.36×105x=0.150⋅2.10×106−2.10×106x
3.36×105x+2.10×106x=0.150⋅2.10×106
(3.36×105+2.10×106)x=0.150⋅2.10×106
6. Calculate the Right Side:
0.150⋅2.10×106=315000J
7. Combine the Coefficients:
(3.36×105+2.10×106)=2.4336×106
2.4336×106x=315000
8. Solve for x:
x=3150002.4336×106≈0.129kg≈129g
9. Calculate the Mass of Evaporated Water:
Mass of evaporated water=150g−x≈150g−129g≈21g
Final Answer:
The mass of evaporated water will be closest to 20 g.
- Mass of water (m) = 150 g = 0.150 kg
- Latent heat of fusion of water (L_f) = 3.36×105J/kg
- Latent heat of vaporization of water (L_v) = 2.10×106J/kg
- Let x be the mass of water that turns into ice (in kg).
- The mass of water that evaporates will then be 0.150−x kg.
- The heat lost by the water turning into ice is given by:
Qloss=x⋅Lf
- The heat gained by the water turning into vapor is given by:
Qgain=(0.150−x)⋅Lv
- Since the system is adiabatic, the heat lost by the ice formation equals the heat gained by the vaporization:
x⋅Lf=(0.150−x)⋅Lv
x⋅(3.36×105)=(0.150−x)⋅(2.10×106)
3.36×105x=0.150⋅2.10×106−2.10×106x
3.36×105x+2.10×106x=0.150⋅2.10×106
(3.36×105+2.10×106)x=0.150⋅2.10×106
0.150⋅2.10×106=315000J
(3.36×105+2.10×106)=2.4336×106
2.4336×106x=315000
x=3150002.4336×106≈0.129kg≈129g
Mass of evaporated water=150g−x≈150g−129g≈21g
The mass of evaporated water will be closest to 20 g.
Topper's Solved these Questions
Similar Questions
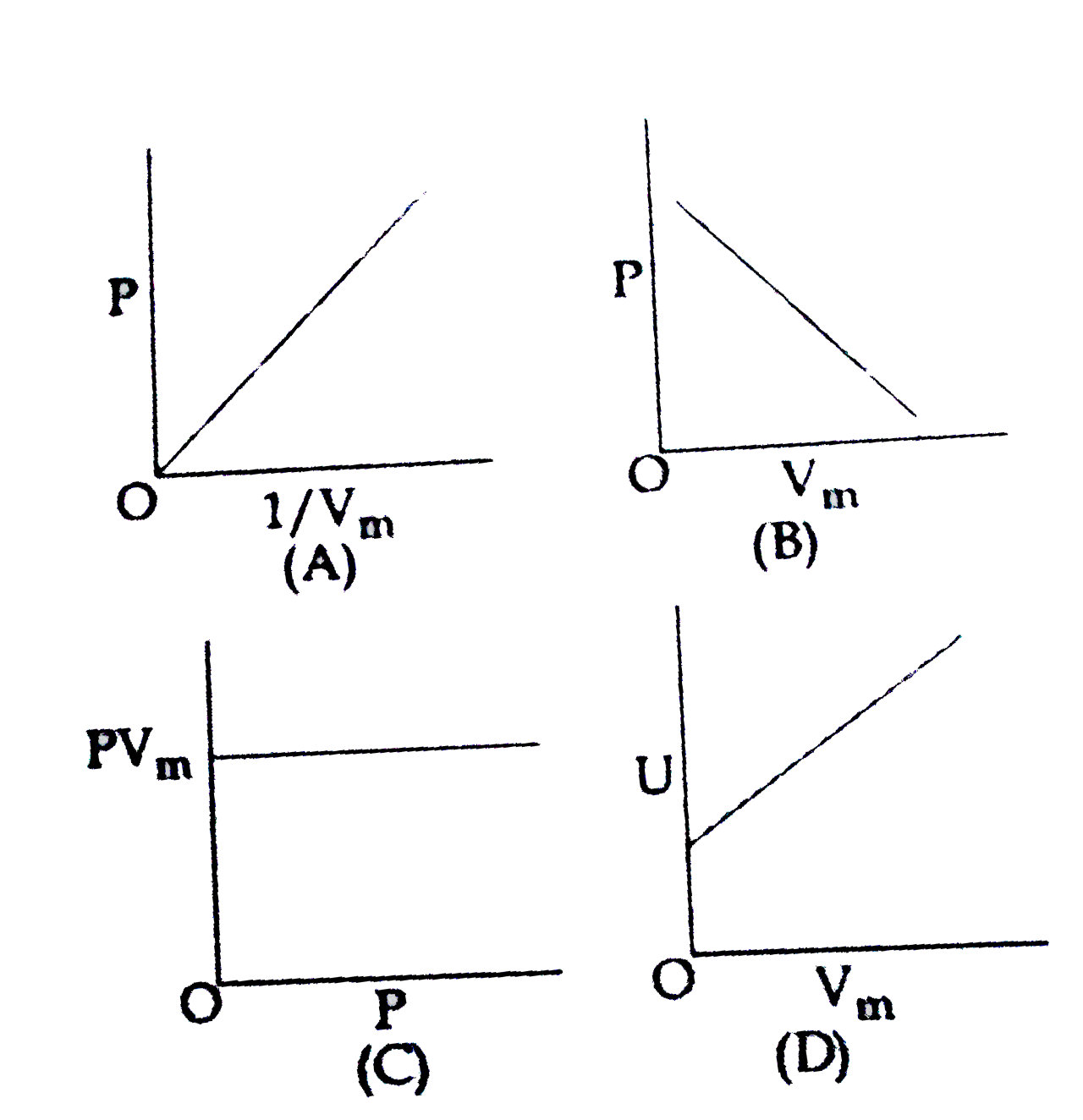
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionA thermally insulated vessel contains 150g of water at 0^(@)C . Then the air from the vessel is pumped out adiabatically. A fraction of water turms into ice and the rest evaporates at 0^(@)C itself. The mass of evaporated water will be closest to : (Latent heat of vaporization of water =2.10xx10^(6)jkg^(-1) and Latent heat of Fusion of water =3.36xx10^(5)jkg^(-1) )
View SolutionSome water at 0^@C is placed in a large insulated enclosure (vessel). The water vapour formed is puped out continuously. What fraction of the water will ultimately freeze, if the latent heat of vapourization is seven times the latent heat of fusion?
View SolutionA thermal insulated vessel contains some water at 0^(@)C . The vessel is connected to a vaccum pump to pum out water vapour. This results in some water getting frozen. It is given latent heat of vaporization of water at 0^(@)C = 21 xx 10^(5) J//kg and latent heat of freezing of water =3.36 xx 10^(5) J//kg . the maximum percentage amount of water vapour that will be solidified in this manner will be:
View SolutionA thermally isolated vessel contains 100g of water at 0∘C when air above the water is pumped out, some of the water freezes and some evaporates at 0∘C itself. Calculate the mass at 0∘C=2.10×106j/kg and latent heat of fusion of ice =3.36×105j/kg.
View SolutionA heater melts 0^@C ice in a bucket completely into water in 6 minutes and then evaporates all that water into steam in 47 minutes 30 sec . If latent heat of fusion of ice is 80 cal//gram , latent heat of steam will be (specific heat of water is 1 cal//gam-^@C )
View SolutionA vessel contains a small amount of water at 0^(@)C . If the air in the vessel is rapidly pumped out, it causes freezing of the water. Why? What percentage of the water in the container can be frozen by this method? Latent heat of vaporization and fusion are L_(V) = 540 cal g^(-1) and L_(f) = 80 cal g^(-1) respectively.
View SolutionFind the result of mixing 1kg of ice at 0^(@)C with 1.5kg of water at 45^(@)C . (Specific latent heat of fusioin of ice =336xx10^(3)Jkg^(-1) )
View SolutionA thermally isolated vessel contains 100g of water at 0∘C. When air above the water is pumped out, some of the water freezes and some evaporates at 0∘C itself. Calculate the mass of the ice formed such that no water is left in the vessel. Latent heat of vaporization of water at 0∘C=2.10×106J/kg and latent heat of fusion of ice =3.36×105J/kg.
View SolutionA non conducting vessel thermally insulated from its surroundings, contains 100 g of water 0∘C. The vessel is connected to a vacuum pump to pump to water vapour. As a result of this, some water is frozen. If the removal of water vapour is continued, what is the maximum amount of water that can be frozen in this manner? Laten heat of vaporisation of water =22.5×105Jkg−1 and latent heat of fusion of ice =3.36×105Jkg−1
View Solution0∘C पर 150g पानी को ऊष्मीय विलग पात्र में रखा गया है। पात्र से वायु को रुद्धोष्म प्रक्रम द्वारा निष्काषित करते है। पानी का एक भाग बर्फ में तथा शेष 0∘C की वाष्प में परिवर्तित हो जाता है। वाष्पित पानी के द्रव्यमान का निकटतम मान होगा (पानी के वाष्पीकरण की गुप्त ऊष्मा =2.10×106Jkg−1 और पानी के गलन की गुप्त ऊष्मा =3.36×105kg−1)
View SolutionA thermally isolated vessel is maintained inside at 0^@C and contains 200 g of water. When the air above the water is pumped out, some of the water freezes while rest of it evaporated at 0^@C itself. Determine the mass of water that freezed. Take, Latent heat of vapourisation of water at 0^@C = 2.19 xx 10^3 J//g Latent heat of fusion of ice = 3.36 xx 10^2 J//g
View Solution7500 cal of heat is supplied to 100g of ice 0∘C. If the latent heat of fusion of ice is 80 cal g−1 and latent heat of vaporization of water is 540 cal g−1, the final temperature of water is
View Solution
