A circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
Br2IπN
Bπr2IN
Bπr2(I)N
Zero
The correct Answer is:B
To find the torque on a circular coil placed in a magnetic field, we can follow these steps:
1. Identify the Given Parameters:
- Number of turns of the coil, N
- Radius of the coil, r
- Current flowing through the coil, I
- Magnetic field, B=B^i (along the x-direction)
2. Determine the Area of the Coil:
The area A of a circular coil is given by the formula:
A=πr2
3. Calculate the Magnetic Moment m:
The magnetic moment m of the coil is given by:
m=N⋅I⋅A
Substituting the area A:
m=N⋅I⋅(πr2)
4. Determine the Direction of the Magnetic Moment:
Since the coil is in the xz-plane, the area vector A (and hence the magnetic moment m) will be perpendicular to the plane of the coil. Therefore, it points in the y-direction:
m=N⋅I⋅πr2^j
5. Calculate the Torque τ:
The torque τ on the coil in a magnetic field is given by the cross product:
τ=m×B
Substituting the values of m and B:
τ=(N⋅I⋅πr2^j)×(B^i)
6. Evaluate the Cross Product:
Using the right-hand rule and the properties of cross products:
τ=N⋅I⋅πr2⋅B(^j×^i)
Since ^j×^i=−^k, we have:
τ=−N⋅I⋅πr2⋅B^k
7. Magnitude of the Torque:
The magnitude of the torque is:
|τ|=N⋅I⋅πr2⋅B
Final Result:
The torque on the coil due to the magnetic field is:
|τ|=N⋅I⋅πr2⋅B
- Number of turns of the coil, N
- Radius of the coil, r
- Current flowing through the coil, I
- Magnetic field, B=B^i (along the x-direction)
The area A of a circular coil is given by the formula:
A=πr2
The magnetic moment m of the coil is given by:
m=N⋅I⋅A
Substituting the area A:
m=N⋅I⋅(πr2)
Since the coil is in the xz-plane, the area vector A (and hence the magnetic moment m) will be perpendicular to the plane of the coil. Therefore, it points in the y-direction:
m=N⋅I⋅πr2^j
The torque τ on the coil in a magnetic field is given by the cross product:
τ=m×B
Substituting the values of m and B:
τ=(N⋅I⋅πr2^j)×(B^i)
Using the right-hand rule and the properties of cross products:
τ=N⋅I⋅πr2⋅B(^j×^i)
Since ^j×^i=−^k, we have:
τ=−N⋅I⋅πr2⋅B^k
The magnitude of the torque is:
|τ|=N⋅I⋅πr2⋅B
The torque on the coil due to the magnetic field is:
|τ|=N⋅I⋅πr2⋅B
Topper's Solved these Questions
Similar Questions
A circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA circular coil of 20turns and radius 10cm carries a current of 5A. It is placed in a uniform magnetic field of 0⋅10T. Find the torque acting on the coil when the magnetic field is applied (a) normal to the plane of the coil (b) in the plane of coil. Also find out the total force acting on the coil.
View SolutionA circular coil of closely wound N terns and radius r carriers a current I.
Write the expressions for the following :
(i) the magnetic field at its centre
(ii) the magnetic moment of this coilView SolutionA circular coil of 100 turns has a radius of 10 cm and carries a current of 5 A. Determine the magnetic field at the centre of the coil and at a point on the axis of the coil at a distance of 5 cm from its centre.
View SolutionA circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
View SolutionA circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
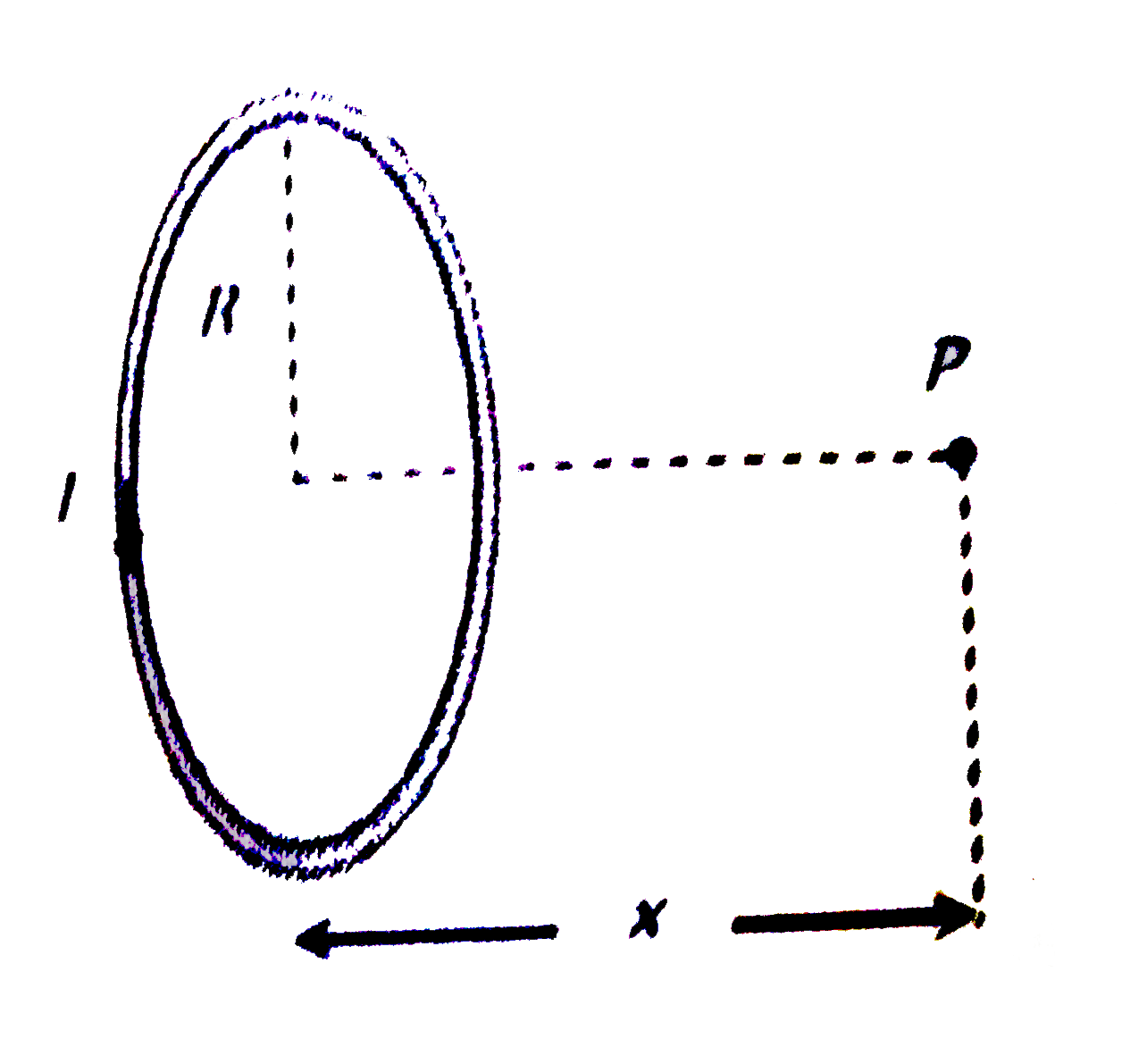 View Solution
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA moving coil galvanometer has a 50-turn coil of size 2cm×2cm. It is suspended between the magnetic poles producing a magnetic field of 0.5T. Find the torque on the coil due to the magnetic field when a current of 20mA passes through it.
View Solution

