A rocket has to be launched from earh in such a way that it never returns. If E is the minimum energy delivered by the rocket launcher what should be the minimum energy that the launcher should have if the same rocket has launcher from the surface of the moon ? Assume that the density of the earth and the moon are equal and that the earth's volume is times the volume of the moon
The correct Answer is:A
To solve the problem, we need to determine the minimum energy required for a rocket to be launched from the surface of the Moon such that it never returns, given that the same rocket requires energy E when launched from the surface of the Earth.
1. Understanding Escape Energy from Earth:
The minimum energy E required for a rocket to escape Earth's gravitational field can be expressed using the formula for gravitational potential energy and kinetic energy. The total mechanical energy at the surface of the Earth is given by:
E=GMEarthmREarth
where G is the gravitational constant, MEarth is the mass of the Earth, m is the mass of the rocket, and REarth is the radius of the Earth.
2. Relating the Masses and Radii of Earth and Moon:
We know that the volume of the Earth is 64 times that of the Moon, and both have the same density. Therefore, we can express the relationship between their masses and radii as follows:
VEarth=64VMoon⟹MEarthMMoon=64
Since density ρ is mass per unit volume and is the same for both:
MMoonMEarth=164
3. Finding the Radius Relationship:
The volume of a sphere is given by V=43πR3. Thus, the ratio of the volumes gives us:
R3EarthR3Moon=64⟹REarthRMoon=4
4. Escape Energy from Moon:
The escape energy E′ from the Moon can be expressed similarly:
E′=GMMoonmRMoon
5. Finding the Ratio of Energies:
To find the ratio of the escape energies E′E:
E′E=GMMoonRMoon⋅REarthGMEarth
Substituting the mass and radius relationships:
E′E=G(164MEarth)RMoon⋅REarthGMEarth
Simplifying this gives:
E′E=164⋅REarthRMoon
Since REarthRMoon=4:
E′E=164⋅4=464=116
6. Final Result:
Therefore, the minimum energy E′ required for the rocket to escape from the surface of the Moon is:
E′=E16
Conclusion:
The minimum energy that the launcher should have if the same rocket is launched from the surface of the Moon is E16.
The minimum energy E required for a rocket to escape Earth's gravitational field can be expressed using the formula for gravitational potential energy and kinetic energy. The total mechanical energy at the surface of the Earth is given by:
E=GMEarthmREarth
where G is the gravitational constant, MEarth is the mass of the Earth, m is the mass of the rocket, and REarth is the radius of the Earth.
We know that the volume of the Earth is 64 times that of the Moon, and both have the same density. Therefore, we can express the relationship between their masses and radii as follows:
VEarth=64VMoon⟹MEarthMMoon=64
Since density ρ is mass per unit volume and is the same for both:
MMoonMEarth=164
The volume of a sphere is given by V=43πR3. Thus, the ratio of the volumes gives us:
R3EarthR3Moon=64⟹REarthRMoon=4
The escape energy E′ from the Moon can be expressed similarly:
E′=GMMoonmRMoon
To find the ratio of the escape energies E′E:
E′E=GMMoonRMoon⋅REarthGMEarth
Substituting the mass and radius relationships:
E′E=G(164MEarth)RMoon⋅REarthGMEarth
Simplifying this gives:
E′E=164⋅REarthRMoon
Since REarthRMoon=4:
E′E=164⋅4=464=116
Therefore, the minimum energy E′ required for the rocket to escape from the surface of the Moon is:
E′=E16
The minimum energy that the launcher should have if the same rocket is launched from the surface of the Moon is E16.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A capillary tube is taken from the Earth to the surface of the moon. The rise of the liquid column on the Moon (acceleration due to gravity on the Earth is 6 times that of the Moon) is
Asix times that on the earth's surfaceB1/6 that on tha earth surfaceCequal on that of the earth surfaceDzero
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
View SolutionThe diameter of the moon is approximately one-fourth of the diameter of the earth.What fraction of the volume of the earth is the volume of the moon?
View SolutionEscape velocity from the surface of moon is less than that from the surface of earth because the moon has no atmosphere while earth has a very dense one.
View SolutionWhy rockets are launched from west to east in the equatorial plane?
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :
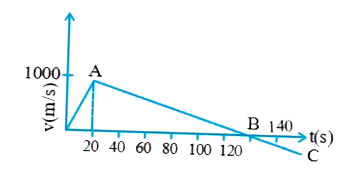
View SolutionAssuming that the moon is a sphere of the same mean density as that of the earth and one quarter of its radius the length of a seconds on the moon (its length on the earth's surface is 99.2cm) is .
View SolutionCalculate the distance from the earth to the point where the gravitational field due to the earth and the moon cancel out. Given that the earth-moon distance is 3.8×108m and the mass of earth is 81 times that of moon.
View Solution
