A solid sphere of mass 'M' and radius 'a' is surrounded by a uniform concentric spherical shell of thickness 2a and mass 2M. The gravitational field at distance '3a' from the centre will be :
2GM9a2
GM9a2
GM3a2
2GM3a2
The correct Answer is:C
To find the gravitational field at a distance 3a from the center of a solid sphere of mass M and radius a, surrounded by a uniform concentric spherical shell of thickness 2a and mass 2M, we can follow these steps:
Step 1: Understand the Configuration
We have a solid sphere of mass M and radius a. Surrounding this sphere is a spherical shell of thickness 2a and mass 2M. The inner radius of the shell is a and the outer radius is 3a.
Step 2: Identify the Point of Interest
We need to calculate the gravitational field at a distance 3a from the center of the solid sphere.
Step 3: Apply the Gravitational Field Formula
For a point outside a solid sphere or a spherical shell, the gravitational field g can be calculated using the formula:
g=GMr2
where G is the gravitational constant, M is the mass enclosed within the radius r, and r is the distance from the center.
Step 4: Calculate the Gravitational Field Due to the Solid Sphere
At a distance 3a, the gravitational field due to the solid sphere (mass M) is:
gsphere=GM(3a)2=GM9a2
Step 5: Calculate the Gravitational Field Due to the Spherical Shell
The entire mass of the spherical shell (mass 2M) can be treated as if it is concentrated at its center when calculating the gravitational field outside it. Therefore, at a distance 3a, the gravitational field due to the shell is:
gshell=G(2M)(3a)2=2GM9a2
Step 6: Combine the Gravitational Fields
The total gravitational field at a distance 3a from the center is the sum of the fields due to the solid sphere and the spherical shell:
gtotal=gsphere+gshell=GM9a2+2GM9a2=3GM9a2=GM3a2
Final Answer
Thus, the gravitational field at a distance 3a from the center is:
GM3a2
We have a solid sphere of mass M and radius a. Surrounding this sphere is a spherical shell of thickness 2a and mass 2M. The inner radius of the shell is a and the outer radius is 3a.
We need to calculate the gravitational field at a distance 3a from the center of the solid sphere.
For a point outside a solid sphere or a spherical shell, the gravitational field g can be calculated using the formula:
g=GMr2
where G is the gravitational constant, M is the mass enclosed within the radius r, and r is the distance from the center.
At a distance 3a, the gravitational field due to the solid sphere (mass M) is:
gsphere=GM(3a)2=GM9a2
The entire mass of the spherical shell (mass 2M) can be treated as if it is concentrated at its center when calculating the gravitational field outside it. Therefore, at a distance 3a, the gravitational field due to the shell is:
gshell=G(2M)(3a)2=2GM9a2
The total gravitational field at a distance 3a from the center is the sum of the fields due to the solid sphere and the spherical shell:
gtotal=gsphere+gshell=GM9a2+2GM9a2=3GM9a2=GM3a2
Thus, the gravitational field at a distance 3a from the center is:
GM3a2
Topper's Solved these Questions
Similar Questions
A solid sphere of radius a and mass m is surrounded by cocentric spherical shell of thickness 2a and mass 2m the gravitational field at a distance 3a from their centres is
View SolutionA uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a.Find the gravitational field at a distance a. 32a from the center , b. 52a from the center.
View SolutionA uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a. Find the gravitational field at a distance a). 3/2 a from the centre , b). 5/2 as from the centre.
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass but radius 2R. A point mass is kept at a distance x(>R) in the region bounded by spheres as shown in the figure . The net gravitational force on the particle is

View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.

What time will it take to move from A to B?
View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.
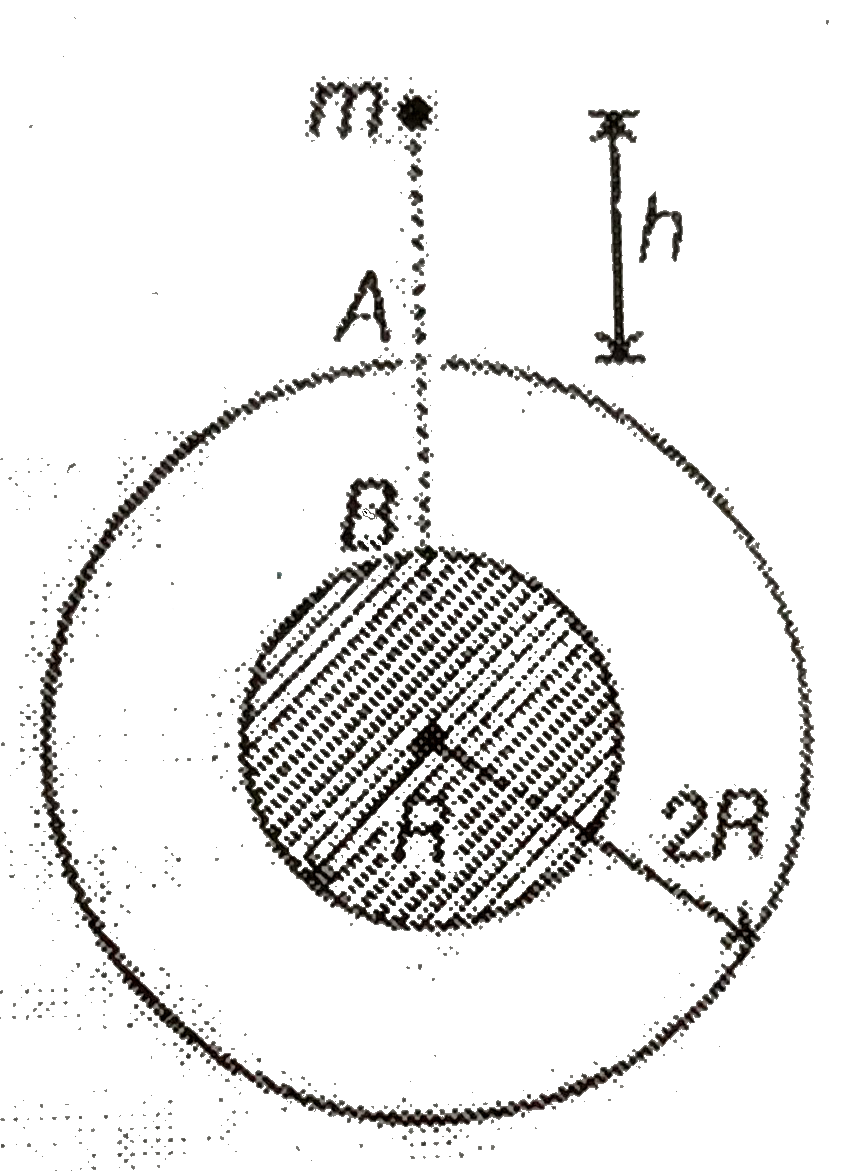
What speed will it collide at B?
View Solution
