A ball is through vertically up (taken as +z-axis) from the ground. The correct momentum-height (p-h) diagram is :
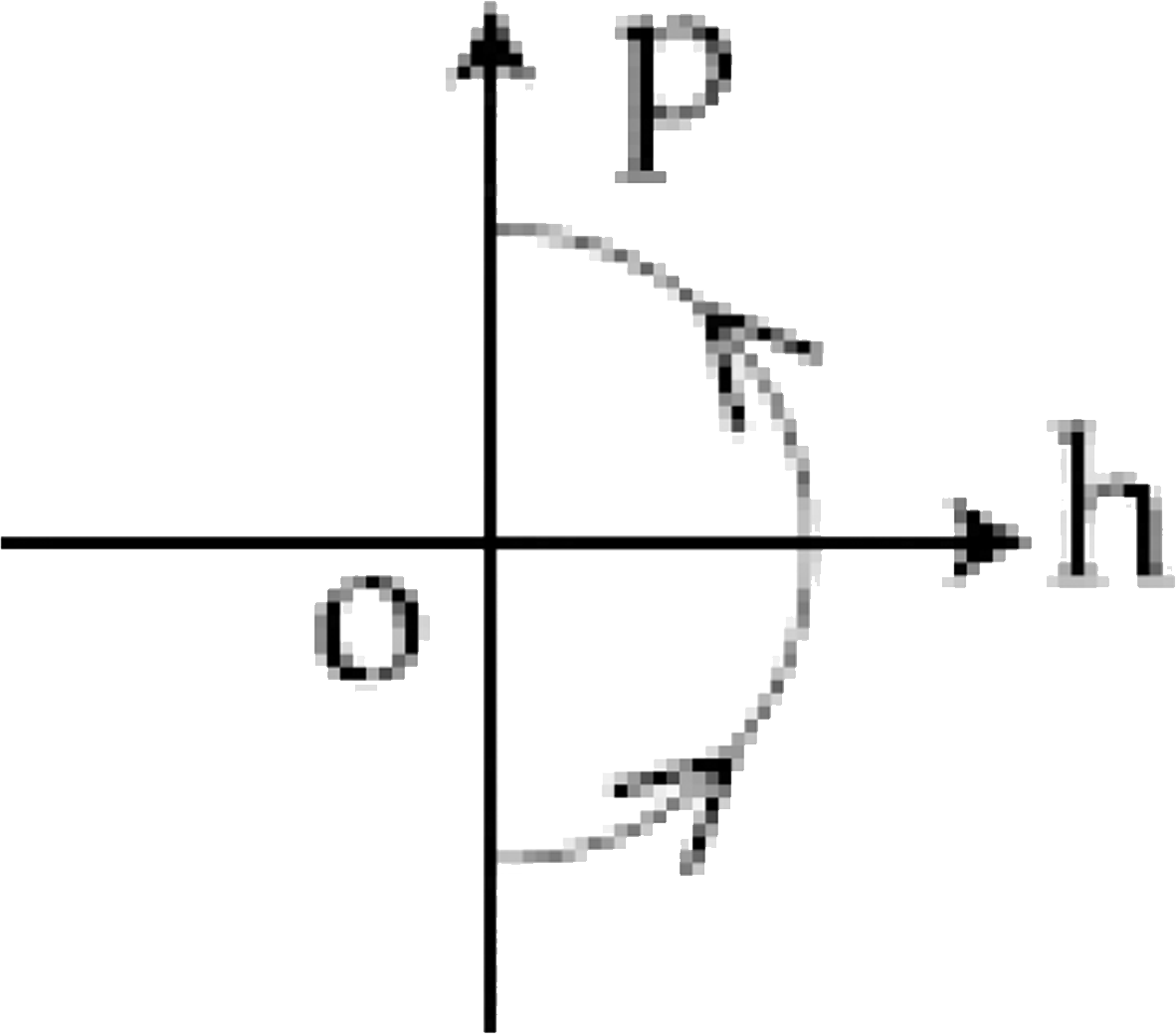
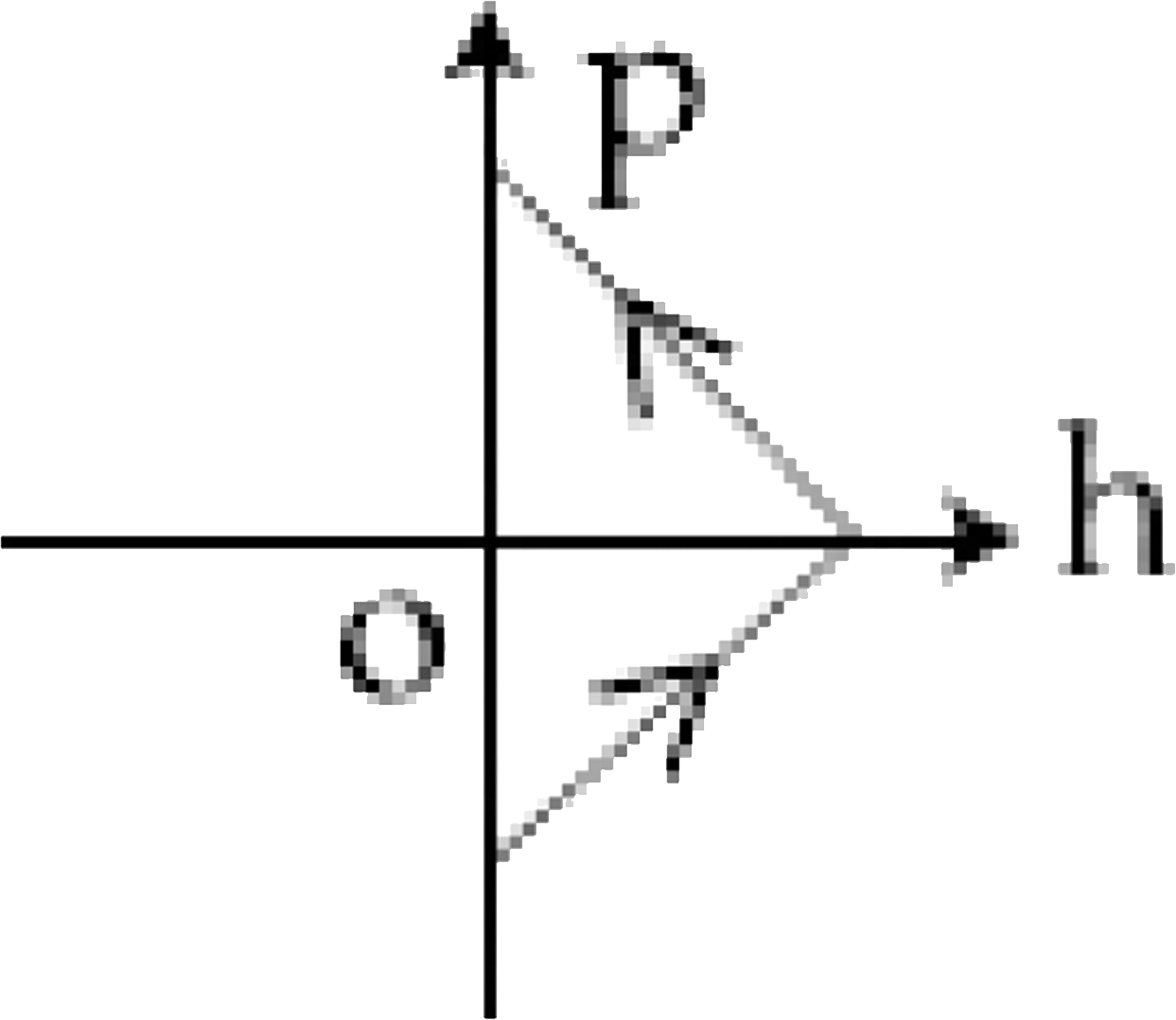
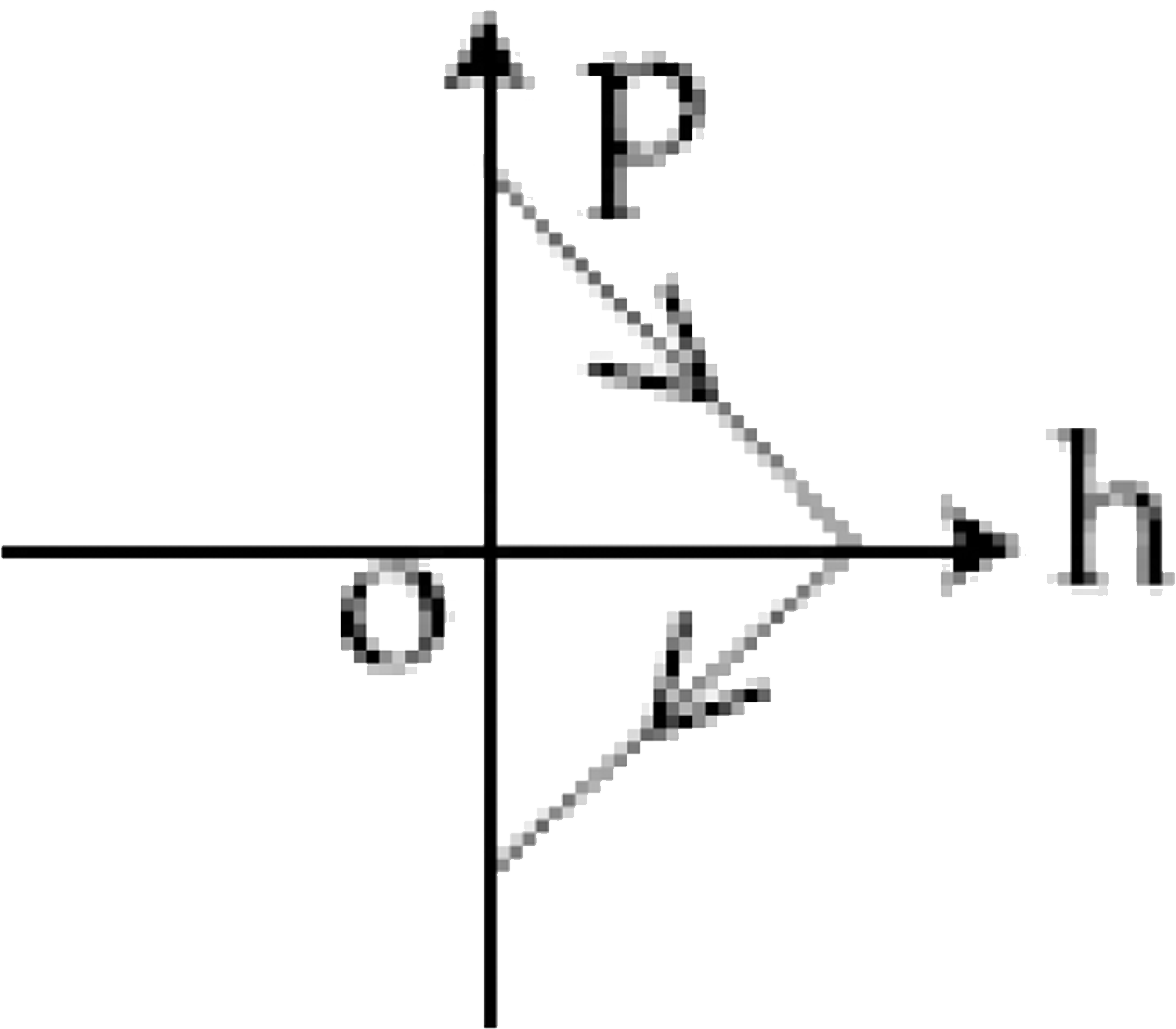
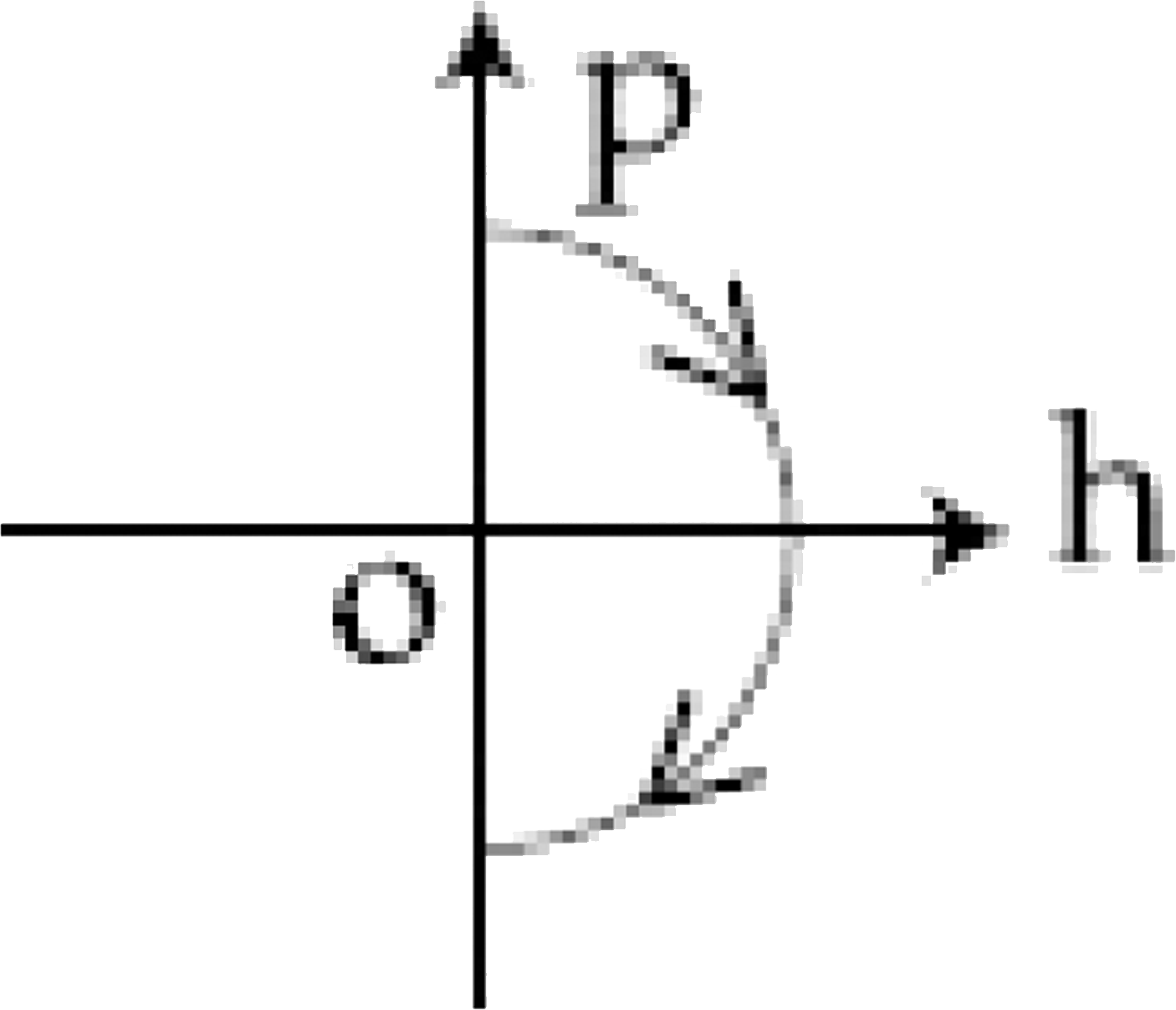
The correct Answer is:D
To solve the problem of determining the correct momentum-height (p-h) diagram for a ball thrown vertically upwards, we can follow these steps:
1. Understanding Initial Conditions:
- A ball is thrown vertically upwards from the ground with an initial velocity v0.
- The momentum p of the ball at the initial height (ground level, h=0) is given by:
p=m⋅v0
- Since the ball is moving upwards, the momentum is positive.
2. Analyzing Motion:
- As the ball rises, it experiences a gravitational force acting downwards, which causes its velocity to decrease.
- At the maximum height h, the velocity becomes zero, and thus the momentum also becomes zero:
p=0ath=hmax
3. Momentum as a Function of Height:
- The relationship between momentum and height can be derived from the equations of motion. Using the equation:
v2=u2−2gh
- Here, v is the final velocity (which becomes zero at maximum height), u is the initial velocity v0, and g is the acceleration due to gravity.
- Rearranging gives:
0=v20−2ghmax⟹hmax=v202g
4. Momentum-Height Relationship:
- The momentum can be expressed as:
p=m⋅v=m⋅√v20−2gh
- Squaring both sides gives:
p2=m2(v20−2gh)
- This shows that p2 is a linear function of h, indicating that the momentum decreases as height increases.
5. Graphing the Relationship:
- At h=0, p is maximum (p=mv0).
- As h increases to hmax, p decreases to zero.
- After reaching maximum height, as the ball falls back down, momentum becomes negative, increasing in magnitude until it reaches −mv0 when it returns to the ground.
6. Identifying the Correct Option:
- The correct momentum-height graph will show momentum starting at a maximum positive value at h=0, decreasing to zero at maximum height, and then becoming negative as the ball falls back down.
- This behavior corresponds to option D.
Final Answer:
The correct momentum-height (p-h) diagram is option D.
- A ball is thrown vertically upwards from the ground with an initial velocity v0.
- The momentum p of the ball at the initial height (ground level, h=0) is given by:
p=m⋅v0
- Since the ball is moving upwards, the momentum is positive.
- As the ball rises, it experiences a gravitational force acting downwards, which causes its velocity to decrease.
- At the maximum height h, the velocity becomes zero, and thus the momentum also becomes zero:
p=0ath=hmax
- The relationship between momentum and height can be derived from the equations of motion. Using the equation:
v2=u2−2gh
- Here, v is the final velocity (which becomes zero at maximum height), u is the initial velocity v0, and g is the acceleration due to gravity.
- Rearranging gives:
0=v20−2ghmax⟹hmax=v202g
- The momentum can be expressed as:
p=m⋅v=m⋅√v20−2gh
- Squaring both sides gives:
p2=m2(v20−2gh)
- This shows that p2 is a linear function of h, indicating that the momentum decreases as height increases.
- At h=0, p is maximum (p=mv0).
- As h increases to hmax, p decreases to zero.
- After reaching maximum height, as the ball falls back down, momentum becomes negative, increasing in magnitude until it reaches −mv0 when it returns to the ground.
- The correct momentum-height graph will show momentum starting at a maximum positive value at h=0, decreasing to zero at maximum height, and then becoming negative as the ball falls back down.
- This behavior corresponds to option D.
The correct momentum-height (p-h) diagram is option D.
Topper's Solved these Questions
Similar Questions
A ball is thrown vertically upwards from the ground. If T1 and T2 are the respective time taken in going up and coming down, and the air resistance is not ignored, then
View SolutionAn open elevator is ascending with constant speed v=10m/s. A ball is thrown vertically up by a boy on the lift when he is at a height h=10m from the ground. The velocity of projection is v=30m/s with respect to elevator. Find
(a) the maximum height attained by the ball.
(b) the time taken by the ball to meet the elevator again.
(c) time taken by the ball to reach the ground after crossing the elevator.
View Solution
Knowledge Check
A bal is thrown vertically upwards from the ground. It crosses a point at the height of 25 m twice at an interval of 4 secs. The ball was thrown with the velocity of
A20 m/sB25 m/sC30 m/sD35 m/sA ball of mass m is thrown vertically up with an initial velocity so as to reach a height h.The correct statement is :
APotential energy of the ball at the ground is mgh.BKinetic energy of the ball at ground is zeroCKinetic energy of the ball at the highest point is mgh .DPotential enengy of the ball at the highest point is mgh.
A ball of mass 'm' is thrown vertically up-ward from the ground and reached a height 'h' before momentarily coming to rest , If 'g' is acceleration due to gravity . What is the impulse received by the ball due to gravity force during its flight ? (neglect air resistance )
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionA particle is thrown vertically upward with a speed u from the top of a tower of height h from ground level, If after first impact with ground it just reaches to height h from ground the coeffecient of restitution for the collision is :−
View SolutionA body falling a vertically up with initial velocity 52 m/s from the ground passes twice a point at h height above at an interval of 10 s. The height h is (g=10m/s2)
View SolutionA stone projected vertically upwards from the ground reaches a maximum height h. When it is at a height (3h)/(4), the ratio of its kinetic and potential energies is
View Solution
