A very long solenoid of radius R is carrying current I(t)=kte−αt , as a function of time (t≥0). Counter clockwise current is taken to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid. the current induced inthe outer coil is correctly depicted, as function of time by :

The correct Answer is:A
To solve the problem, we need to analyze the situation involving a long solenoid carrying a time-dependent current and the induced current in a concentric conducting coil placed in its equatorial plane.
1. Identify the Current in the Solenoid:
The current in the solenoid is given by:
I(t)=kte−αt
where k and α are constants.
2. Determine the Magnetic Field Inside the Solenoid:
The magnetic field B inside a long solenoid carrying current I is given by:
B=μ0nI
where μ0 is the permeability of free space and n is the number of turns per unit length. Since the solenoid is long and the current varies with time, we substitute I(t):
B(t)=μ0n(kte−αt)
3. Calculate the Magnetic Flux Through the Coil:
The area A of the circular coil of radius 2R is:
A=π(2R)2=4πR2
The magnetic flux Φ through the coil is given by:
Φ(t)=B(t)⋅A=μ0n(kte−αt)⋅(4πR2)
Therefore,
Φ(t)=4πμ0nktR2e−αt
4. Apply Faraday's Law of Induction:
According to Faraday's law, the induced emf E in the coil is the negative rate of change of magnetic flux:
E=−dΦdt
5. Differentiate the Flux:
To find the induced emf, we differentiate Φ(t):
dΦdt=4πμ0nR2(ke−αt−kαte−αt)
Simplifying this gives:
dΦdt=4πμ0nR2ke−αt(1−αt)
Thus, the induced emf is:
E=−4πμ0nR2ke−αt(1−αt)
6. Determine the Induced Current:
If the resistance of the coil is Rc, the induced current Iind can be expressed as:
Iind=ERc=−4πμ0nR2ke−αt(1−αt)Rc
7. Analyze the Behavior of the Induced Current:
- At t=0:
Iind(0)=−4πμ0nR2kRc
- At t=1/α (where 1−αt=0):
Iind(1/α)=0
- As t→∞:
Iind→0
Conclusion:
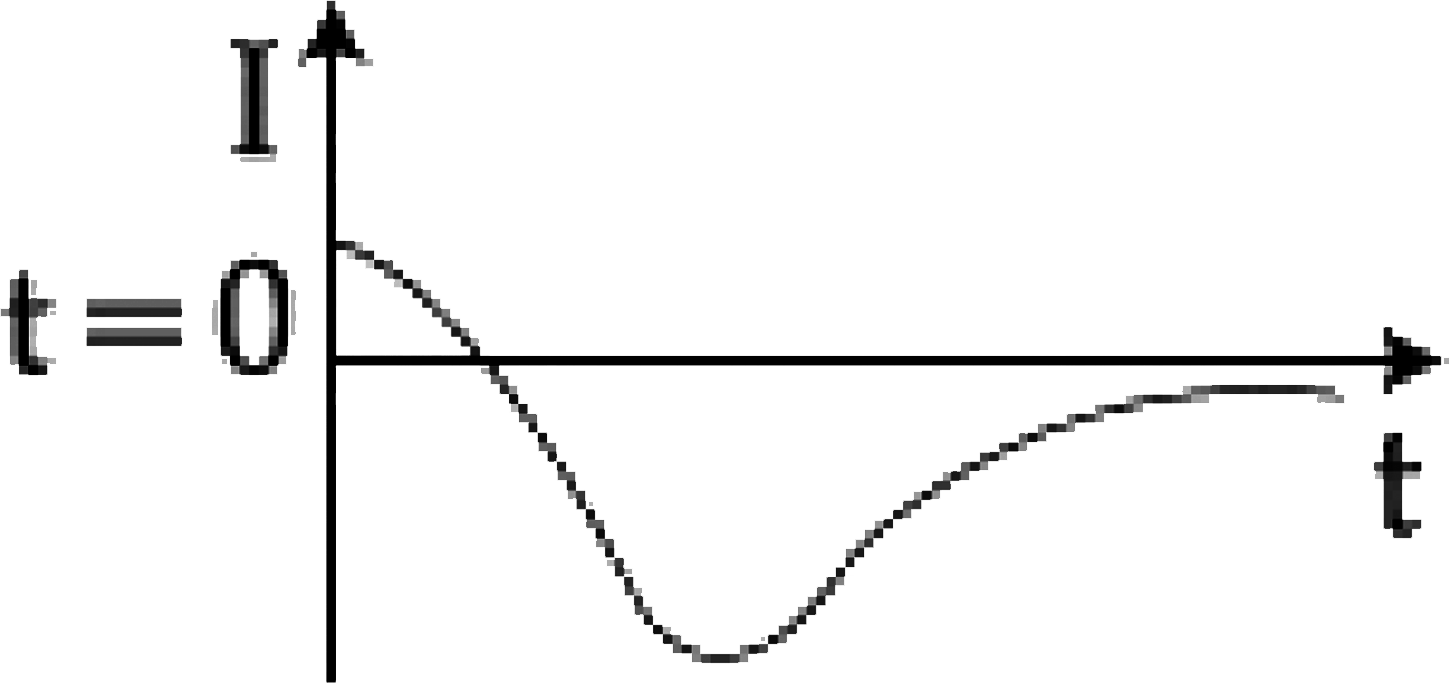
The induced current starts at a negative value, becomes zero at t=1/α, and approaches zero as t increases. The correct depiction of the induced current as a function of time is represented by a curve that starts negative, crosses zero, and approaches zero again.
The current in the solenoid is given by:
I(t)=kte−αt
where k and α are constants.
The magnetic field B inside a long solenoid carrying current I is given by:
B=μ0nI
where μ0 is the permeability of free space and n is the number of turns per unit length. Since the solenoid is long and the current varies with time, we substitute I(t):
B(t)=μ0n(kte−αt)
The area A of the circular coil of radius 2R is:
A=π(2R)2=4πR2
The magnetic flux Φ through the coil is given by:
Φ(t)=B(t)⋅A=μ0n(kte−αt)⋅(4πR2)
Therefore,
Φ(t)=4πμ0nktR2e−αt
According to Faraday's law, the induced emf E in the coil is the negative rate of change of magnetic flux:
E=−dΦdt
To find the induced emf, we differentiate Φ(t):
dΦdt=4πμ0nR2(ke−αt−kαte−αt)
Simplifying this gives:
dΦdt=4πμ0nR2ke−αt(1−αt)
Thus, the induced emf is:
E=−4πμ0nR2ke−αt(1−αt)
If the resistance of the coil is Rc, the induced current Iind can be expressed as:
Iind=ERc=−4πμ0nR2ke−αt(1−αt)Rc
- At t=0:
Iind(0)=−4πμ0nR2kRc
- At t=1/α (where 1−αt=0):
Iind(1/α)=0
- As t→∞:
Iind→0
The induced current starts at a negative value, becomes zero at t=1/α, and approaches zero as t increases. The correct depiction of the induced current as a function of time is represented by a curve that starts negative, crosses zero, and approaches zero again.
Topper's Solved these Questions
Similar Questions
A very long solenoid of radius R is carrying current I(t)=kte−αt , as a function of time (t≥0). Counter clockwise current is taken to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid. the current induced inthe outer coil is correctly depicted, as function of time by :
View SolutionA small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
View Solution
Knowledge Check
A circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
AzeroB3.4 NmC3.8 NmD4.4 NmA circular coil of 25 turns and radius of 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of coil. If the current in the coil is 5 A, then total torque experienced by the coil is
A1.5NmB2.5NmC3.5NmDzero
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA current I flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
View SolutionA non uniform magnetic field B=B0tˆi in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
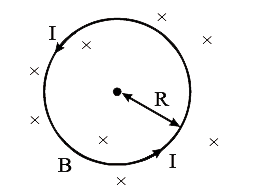
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
View Solution
