The elastic limit of brass is 379MPa. What should be the minimum diameter of a brass rod if it is to support a 400 N load without exceeding its elastic limit?
1.00 mm
1.16 mm
0.90 mm
1.36 mm
The correct Answer is:C
To solve the problem, we need to determine the minimum diameter of a brass rod that can support a load of 400 N without exceeding its elastic limit of 379 MPa.
1. Understand the Concept of Stress:
Stress is defined as the force applied per unit area. The formula for stress (σ) is given by:
σ=FA
where F is the force applied, and A is the cross-sectional area.
2. Relate Area to Diameter:
For a circular cross-section (like a rod), the area A can be expressed in terms of the diameter d:
A=πd24
3. Substitute Area into the Stress Formula:
Substituting the expression for area into the stress formula gives:
σ=Fπd24=4Fπd2
4. Set Stress Equal to the Elastic Limit:
We know the elastic limit of brass is 379 MPa, which can be converted to Pascals:
379 MPa=379×106 Pa
Setting the stress equal to the elastic limit:
4Fπd2=379×106
5. Substitute the Load into the Equation:
The load F is given as 400 N. Substituting this value into the equation:
4×400πd2=379×106
6. Rearranging the Equation:
Rearranging the equation to solve for d2:
d2=4×400π×(379×106)
7. Calculate the Right Side:
Calculate the right side of the equation:
d2=1600π×379×106
Using π≈3.14:
d2=16003.14×379×106≈16001.187×109≈1.347×10−6
8. Taking the Square Root:
Now, take the square root to find d:
d=√1.347×10−6≈0.00115 m=1.15 mm
Final Answer:
The minimum diameter of the brass rod should be approximately 1.15 mm.
Stress is defined as the force applied per unit area. The formula for stress (σ) is given by:
σ=FA
where F is the force applied, and A is the cross-sectional area.
For a circular cross-section (like a rod), the area A can be expressed in terms of the diameter d:
A=πd24
Substituting the expression for area into the stress formula gives:
σ=Fπd24=4Fπd2
We know the elastic limit of brass is 379 MPa, which can be converted to Pascals:
379 MPa=379×106 Pa
Setting the stress equal to the elastic limit:
4Fπd2=379×106
The load F is given as 400 N. Substituting this value into the equation:
4×400πd2=379×106
Rearranging the equation to solve for d2:
d2=4×400π×(379×106)
Calculate the right side of the equation:
d2=1600π×379×106
Using π≈3.14:
d2=16003.14×379×106≈16001.187×109≈1.347×10−6
Now, take the square root to find d:
d=√1.347×10−6≈0.00115 m=1.15 mm
The minimum diameter of the brass rod should be approximately 1.15 mm.
Topper's Solved these Questions
Similar Questions
If the elastic limit of copper is 1.5×108N/m2,determine the minimum diameter a copper wire can have under a load of10.0kg force , if its elastic limit is not to be exceeded.
View SolutionA cast iron column has internal diameter of 200 mm. What sholud be the minimum external diameter so that it may carry a load of 1.6MN without the stress exceeding 90N/mm2?
View Solution
Knowledge Check
A steel wire can support a maximum load of W before reaching its elastic limit. How much load can another wire, made out of identical steel, but with a radius one half the radius of the first wire, support before reaching its elastic limit?
AWBW4CW4D4W
The elastic limit of steel is 8×108Nm−2 and its Young modulus 2×1011Nm−2. Find the maximum elongation of a half meter steel wire that can be given without exceeding the elastic limit.
View SolutionThe length of a sonometer wire is 0.75 m and density is 9 × 103 kg/m3. It can bear a stress of 8.1 × 108 N/m2 without exceeding the elastic limit. Then the fundamental frequency that can be produced in the wire is
View SolutionTwo bars A and B of circular cross section, same volume and made of the same material, are subjected to tension. If the diameter of A is half that of B and if the force applied to both the rod is the same and it is in the elastic limit, the ratio of extension of A to that of B will be
View SolutionThe length of a sonometer wire is 0.75 m and density 9×103Kg/m3. It can bear a stress of 8.1×108N/m2 without exceeding the elastic limit . The fundamental that can be produced in the wire , is
View SolutionThe elastic limit of a steel cable is 3.0×108N/m2 and the cross-section area is 4cm2. Find the maximum upward acceleration that can be given to a 900kg elevator supported by the cable if the stress is not to exceed one - third of the elastic limit.
View SolutionThe elastic limit of an elavator cable is 2×109N/m2. The maximum upward acceleration that an elavator of mass 2×103kg can have when supported by a cable whose cross sectional area is 10−4m2, provided the stres in cable would not exceed half to the elastic limit would be
View SolutionThe stress strain graph for a metal wire is shown in the fig. Up to the point E, the wire returns to its original state O along the curve EPO, when it is gradually unloaded. Point B corresponds to the fracture of the wire.
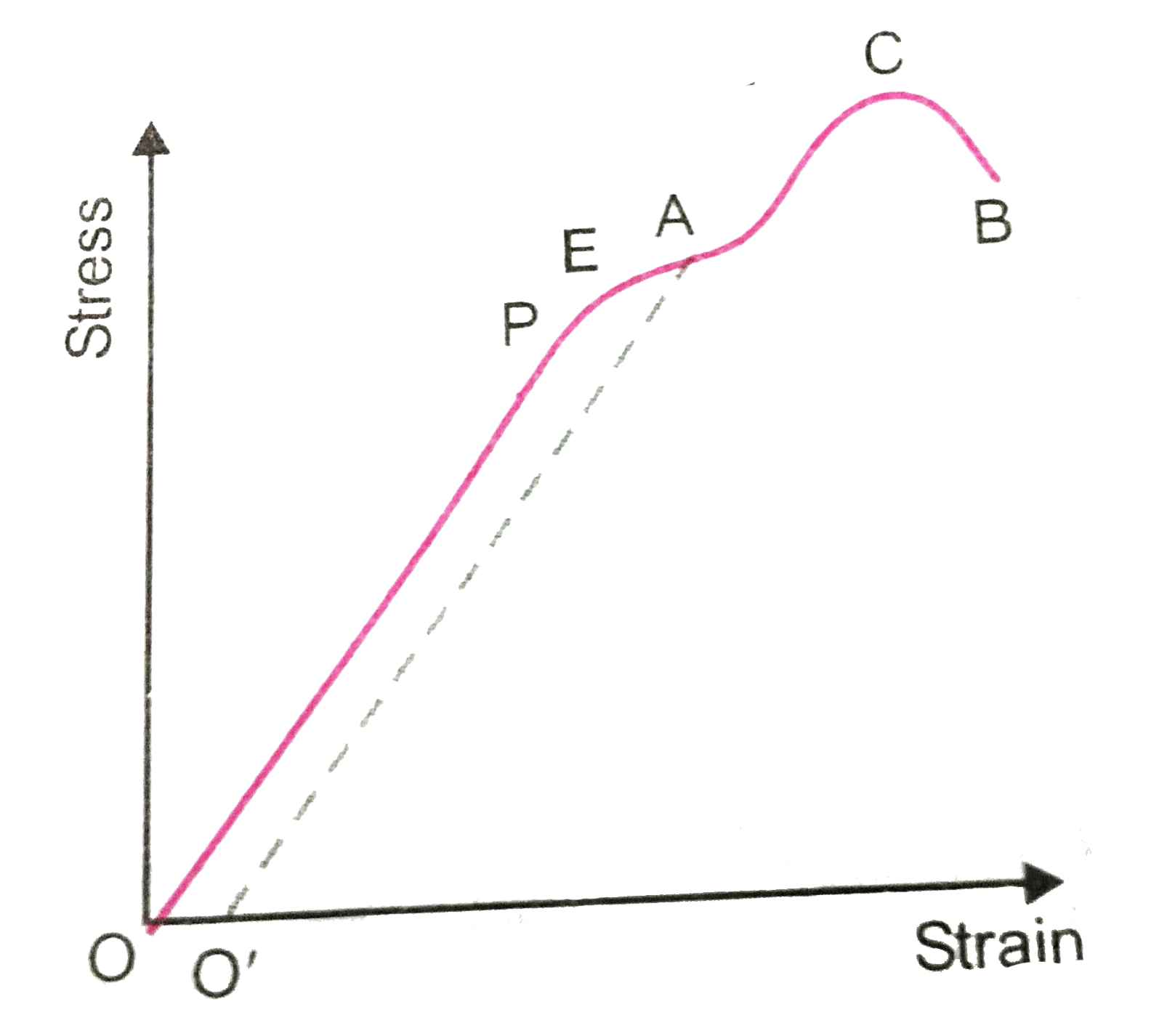
(a) Up to what point on the curve is Hooke's law obeyed? (this point some times called proportional limits).
(b) Which point on the curve corresponding to elastic limit or yield point of the wire?
(c ) Indicate the elastic and plastic regions of the stress-strain graph.
(d) Describe what happens when the wire is loaded up to a stress corresponding to the point A on the graph and then unloaded gradually. In particular explain the dotted curve.
(e) What is peculiar about the portion of the stress- strain graph from C to B? Up to what stress can the wire be subjected without causing fracture?
View Solution
