A uniform rod of length l is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is T(x) at a distance x from the axis. Then which of the following graphs depicts it most closely?




The correct Answer is:C
To solve the problem of determining the tension in a rotating uniform rod, we can follow these steps:
1. Understand the Setup:
- We have a uniform rod of length l rotating about one of its ends with a constant angular speed ω.
- We need to find the tension T(x) at a distance x from the axis of rotation.
2. Consider a Small Element:
- Take a small element of the rod at a distance x with a length dx.
- The mass of this small element can be expressed as:
dm=ml⋅dx
where m is the total mass of the rod.
3. Identify Forces Acting on the Element:
- The tension at distance x is T(x).
- The tension at the next segment x+dx is T(x)+dT.
- The net force acting towards the center (due to rotation) on this small element is:
T(x)−(T(x)+dT)=−dT
4. Centripetal Force Requirement:
- The centripetal force required for the small element to maintain its circular motion is given by:
Fc=dm⋅ω2⋅x=(ml⋅dx)⋅ω2⋅x
5. Set Up the Equation:
- Equating the centripetal force to the change in tension gives:
−dT=ml⋅dx⋅ω2⋅x
- Rearranging this, we have:
dT=−mω2l⋅x⋅dx
6. Integrate to Find Tension:
- Integrate both sides to find T(x):
∫dT=−mω2l∫xdx
- The limits for x will be from 0 to L (the length of the rod), and for T from T(0) to T(L):
T(x)−T(0)=−mω2l(x22)x0
- This gives:
T(x)−T(0)=−mω2l⋅x22
7. Determine Tension at the Ends:
- At x=L, the tension T(L)=0 (since there is no mass at the end of the rod).
- Therefore, we can find T(0):
0−T(0)=−mω2l⋅L22
- Thus, T(0)=mω2L22l.
8. Final Expression for Tension:
- Substituting back, we find:
T(x)=T(0)−mω22lx2=mω2L22l−mω22lx2
- Simplifying gives:
T(x)=mω22l(L2−x2)
9. Graphical Representation:
- The expression T(x)=mω22l(L2−x2) indicates that the tension decreases quadratically from T(0) to 0 at x=L.
- Therefore, the graph of T(x) versus x will be a downward-opening parabola, starting from a maximum value at x=0 and reaching zero at x=L.
- We have a uniform rod of length l rotating about one of its ends with a constant angular speed ω.
- We need to find the tension T(x) at a distance x from the axis of rotation.
- Take a small element of the rod at a distance x with a length dx.
- The mass of this small element can be expressed as:
dm=ml⋅dx
where m is the total mass of the rod.
- The tension at distance x is T(x).
- The tension at the next segment x+dx is T(x)+dT.
- The net force acting towards the center (due to rotation) on this small element is:
T(x)−(T(x)+dT)=−dT
- The centripetal force required for the small element to maintain its circular motion is given by:
Fc=dm⋅ω2⋅x=(ml⋅dx)⋅ω2⋅x
- Equating the centripetal force to the change in tension gives:
−dT=ml⋅dx⋅ω2⋅x
- Rearranging this, we have:
dT=−mω2l⋅x⋅dx
- Integrate both sides to find T(x):
∫dT=−mω2l∫xdx
- The limits for x will be from 0 to L (the length of the rod), and for T from T(0) to T(L):
T(x)−T(0)=−mω2l(x22)x0
- This gives:
T(x)−T(0)=−mω2l⋅x22
- At x=L, the tension T(L)=0 (since there is no mass at the end of the rod).
- Therefore, we can find T(0):
0−T(0)=−mω2l⋅L22
- Thus, T(0)=mω2L22l.
- Substituting back, we find:
T(x)=T(0)−mω22lx2=mω2L22l−mω22lx2
- Simplifying gives:
T(x)=mω22l(L2−x2)
- The expression T(x)=mω22l(L2−x2) indicates that the tension decreases quadratically from T(0) to 0 at x=L.
- Therefore, the graph of T(x) versus x will be a downward-opening parabola, starting from a maximum value at x=0 and reaching zero at x=L.
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA rigid rod of mass m and lengths l, is being rotated in horizontal plane about a vertical axis, passing through one end A. If TA,TBandTC are the tensions in rod at point A, mid point B and point C of rod repsectively, then

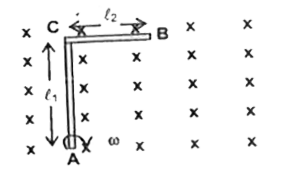
View SolutionFor an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
View SolutionA uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png)
View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View Solution
