A man (mass =50kg) and his son (mass =20kg) are standing on a frictionless surface facing each other , the man pushes his son so that he start moving at a speed of 0.70ms−1 with respect to the man. The speed of the man with respect to the surface is:
0.28ms−1
0.20ms−1
0.47ms−1
0.14ms−1
The correct Answer is:A
To solve the problem, we will apply the principle of conservation of momentum. Here's a step-by-step breakdown of the solution:
Step 1: Understand the system
Initially, both the man and his son are at rest on a frictionless surface. Therefore, the initial momentum of the system is zero.
Step 2: Define the variables
Let:
- Mass of the man, mm=50kg
- Mass of the son, ms=20kg
- Velocity of the man with respect to the ground, vm
- Velocity of the son with respect to the ground, vs
Step 3: Relate the velocities
The son moves with a velocity of 0.70m/s with respect to the man. Therefore, we can express the velocity of the son in terms of the velocity of the man:
vs=vm+0.70
Step 4: Apply conservation of momentum
According to the conservation of momentum:
Initial momentum=Final momentum
Since the initial momentum is zero, we have:
0=mm⋅vm+ms⋅vs
Substituting the values of mm and ms:
0=50⋅vm+20⋅(vm+0.70)
Step 5: Simplify the equation
Expanding the equation gives:
0=50vm+20vm+14
Combining like terms:
0=70vm+14
Step 6: Solve for vm
Rearranging the equation to solve for vm:
70vm=−14
vm=−1470=−0.2m/s
Step 7: Interpret the result
The negative sign indicates that the direction of the man's velocity is opposite to the assumed positive direction (which we took as rightward). Thus, the man is moving at a speed of 0.2m/s to the left.
Final Answer
The speed of the man with respect to the surface is 0.2m/s towards the left.
---
Initially, both the man and his son are at rest on a frictionless surface. Therefore, the initial momentum of the system is zero.
Let:
- Mass of the man, mm=50kg
- Mass of the son, ms=20kg
- Velocity of the man with respect to the ground, vm
- Velocity of the son with respect to the ground, vs
The son moves with a velocity of 0.70m/s with respect to the man. Therefore, we can express the velocity of the son in terms of the velocity of the man:
vs=vm+0.70
According to the conservation of momentum:
Initial momentum=Final momentum
Since the initial momentum is zero, we have:
0=mm⋅vm+ms⋅vs
Substituting the values of mm and ms:
0=50⋅vm+20⋅(vm+0.70)
Expanding the equation gives:
0=50vm+20vm+14
Combining like terms:
0=70vm+14
Rearranging the equation to solve for vm:
70vm=−14
vm=−1470=−0.2m/s
The negative sign indicates that the direction of the man's velocity is opposite to the assumed positive direction (which we took as rightward). Thus, the man is moving at a speed of 0.2m/s to the left.
The speed of the man with respect to the surface is 0.2m/s towards the left.
Topper's Solved these Questions
Similar Questions
To a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
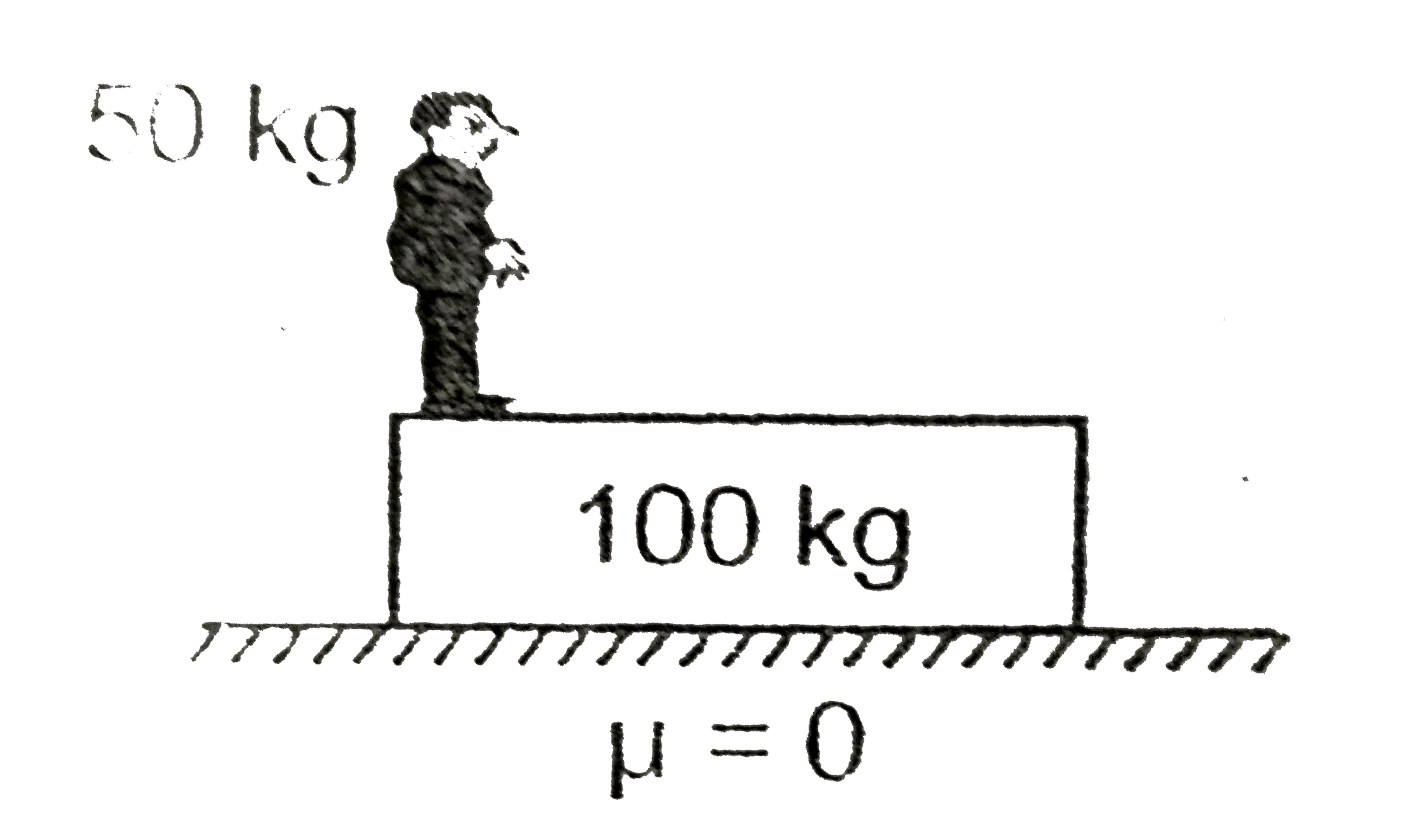
View SolutionA man of mass 50kg us standing on a 100kg plank kept on a fricitonless horizontal floor. Initially both are at rest. If the man starts walking on the plank with speed 6m/s towards right relative to the plank, then amount of muscle energy spent by the man is
View SolutionA man of mass M stands at one end of a plank of length L Which lies at rest on a frictionless surface . The man walks to the other end of the plank. If the mass of the plank is 3M, the distance that the man moves relative to the ground is
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man of mass 60 kg is standing on a horizontal conveyor belt. When the belt is given an acceleration of 1ms−2, the man remains stationary with respect to the moving belt. If g=10ms−2, The net force acting on the man is

View Solution
