0.5 moles of gas A and x moles of gas B exert a pressure of 200 Pa in a container of volume 10m3 at 1000K. Given R is the gas constant in jk−1 ,x is :
2R4+R
2R4−R
4+R2R
4−R2R
To solve the problem step by step, we will use the ideal gas equation, which is given by:
PV=nRT
Where:
- P = pressure (in Pascals)
- V = volume (in cubic meters)
- n = total number of moles of gas
- R = gas constant (in J K−1mol−1)
- T = temperature (in Kelvin)
Step 1: Identify the given values
From the problem statement, we have:
- Pressure, P=200Pa
- Volume, V=10m3
- Temperature, T=1000K
- Moles of gas A, nA=0.5moles
- Moles of gas B, nB=xmoles
Step 2: Write the total number of moles
The total number of moles n is given by:
n=nA+nB=0.5+x
Step 3: Substitute values into the ideal gas equation
Using the ideal gas equation:
PV=nRT
Substituting the known values:
200×10=(0.5+x)×R×1000
Step 4: Simplify the equation
Calculating the left side:
2000=(0.5+x)×R×1000
Step 5: Rearranging the equation
Dividing both sides by 1000:
2=(0.5+x)×R
Step 6: Solve for x
Now, we can express R in terms of the gas constant, which is R=8.314J K−1mol−1 or R=8.314Pa m3K−1mol−1. Thus, we can rewrite the equation:
2=(0.5+x)×8.314
Now, dividing both sides by 8.314:
28.314=0.5+x
Step 7: Calculate x
Calculating 28.314:
28.314≈0.240
Now, we have:
0.240=0.5+x
Subtracting 0.5 from both sides:
x=0.240−0.5
x=−0.260
Since x cannot be negative in this context, we need to check our steps again.
Step 8: Correcting the calculation
Going back to our equation:
2=(0.5+x)×8.314
This means:
0.5+x=28.314
Calculating 28.314 gives approximately 0.240.
So:
x=0.240−0.5
This leads to a contradiction, indicating a miscalculation.
Final Step: Correctly solve for x
Let’s go back to the rearranged equation:
2=(0.5+x)×8.314
Now, we can isolate x:
0.5+x=28.314
Now, let's calculate 28.314 accurately:
28.314≈0.240
Now we can isolate x:
x=28.314−0.5
x=0.240−0.5
This again leads to a negative value, indicating we need to re-evaluate our assumptions about the gases or the problem setup.
- P = pressure (in Pascals)
- V = volume (in cubic meters)
- n = total number of moles of gas
- R = gas constant (in J K−1mol−1)
- T = temperature (in Kelvin)
From the problem statement, we have:
- Pressure, P=200Pa
- Volume, V=10m3
- Temperature, T=1000K
- Moles of gas A, nA=0.5moles
- Moles of gas B, nB=xmoles
The total number of moles n is given by:
n=nA+nB=0.5+x
Using the ideal gas equation:
PV=nRT
Substituting the known values:
200×10=(0.5+x)×R×1000
Calculating the left side:
2000=(0.5+x)×R×1000
Dividing both sides by 1000:
2=(0.5+x)×R
Now, we can express R in terms of the gas constant, which is R=8.314J K−1mol−1 or R=8.314Pa m3K−1mol−1. Thus, we can rewrite the equation:
2=(0.5+x)×8.314
28.314=0.5+x
Calculating 28.314:
28.314≈0.240
0.240=0.5+x
x=0.240−0.5
x=−0.260
Going back to our equation:
2=(0.5+x)×8.314
This means:
0.5+x=28.314
Calculating 28.314 gives approximately 0.240.
x=0.240−0.5
This leads to a contradiction, indicating a miscalculation.
Let’s go back to the rearranged equation:
2=(0.5+x)×8.314
Now, we can isolate x:
0.5+x=28.314
Now, let's calculate 28.314 accurately:
28.314≈0.240
x=28.314−0.5
x=0.240−0.5
This again leads to a negative value, indicating we need to re-evaluate our assumptions about the gases or the problem setup.
Similar Questions
Knowledge Check
Two large glass containers of equal volume each hold 1 mole of gas. Container 1 is filled with hydrogen gas (2g/mol), and container 2 holds helium (4g/mol). If the pressure of the gas in container 1 equals the pressure of the gas in container 2, which of the following is true?
AThe temperature of the gas is container 1 is lower than the temperature of the gas is container 2.BThe temperature of the gas in container 1 is greater than the temperature of the gas in container 2.CThe value of R for the gas in container 1 is 12 the value of R for the gas is container 2.DThe rms speed of the gas molecules in container 1 is greater than the rms speed of the gas molecules in container 2.
The pressure of a gas is 100 k Pa. if it is compressed from 1 m3 to 10dm3 , find the work done .
View SolutionCalculate the moles of an ideal gas at pressure 2atm and volume 1L at a temperature of 97.5K
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
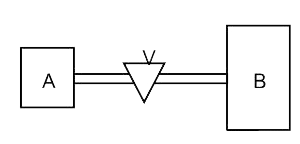
Before the valve V is opened, the ratio of number of moles of gas in A and B is :
View SolutionOne mole of an ideal gas is expanded from a volume of 3L to 5L under a constant pressure of 1 atm. Calculate the work done by the gas.
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
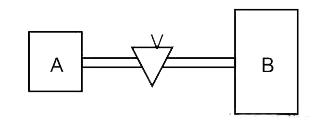
The valve V is adjusted to allow the pressure to equalize, but the temperature of each container is kept constant at the initial value, then the pressure in the two containers is :
View SolutionTwo moles of an ideal monoatomic gas at 5 bar and 300 K are expanded irreversibly up to a final pressure of 1 bar and 240 K against an external pressure of 0.5 bar. The work done by the gas is −xR. The value of x' is
(Here 'R' is gas constant)
View SolutionHalf mole of an ideal monoatomic gas is heated at constant pressure of 1 atm from 20∘C to 90∘C. Work done by gas is close to: (Gas constant R = 8.31 J/mol-K)
View Solution
