Consider the given plots for a reaction obeying Arrhenius equation (0∘C<T<300∘C) : (k and Ea are rate constant and activation energy, respectively)
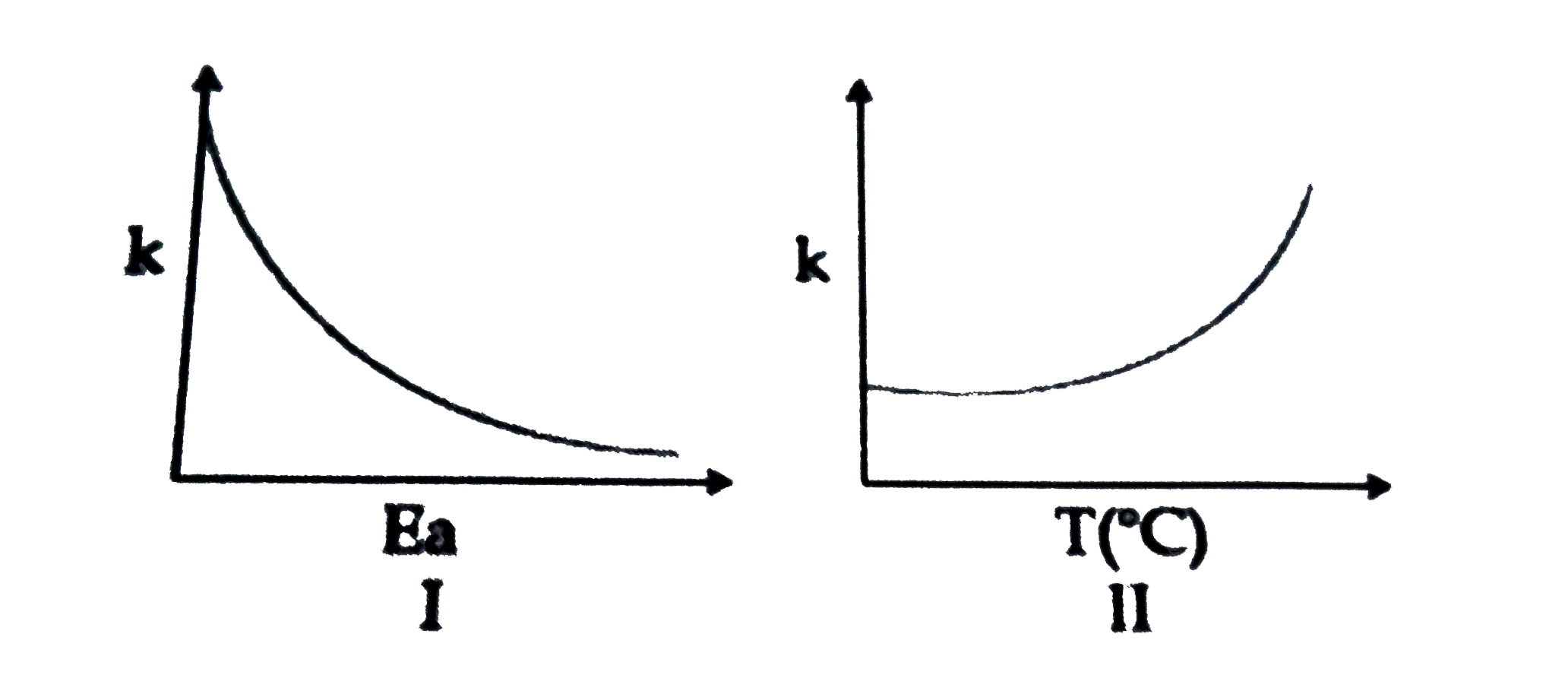
Step by step video & image solution for Consider the given plots for a reaction obeying Arrhenius equation (0^(@)CltTlt300^(@)C) : (k and E_(a) are rate constant and activation energy, respectively) by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider the given plots for a reaction obeying Arrhenius equation (0∘C<T<300∘C) : (kandEa are rate constant and activation energy, respectively) Choose the correct option :
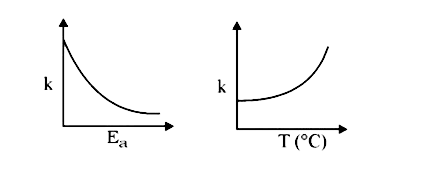
View SolutionConsider the given plots for a reaction obeying Arrhenius equation (k and Ea are rate constant and activation energy, respectively)
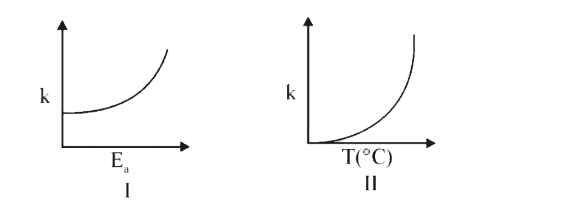
Choose the correct option:
View SolutionIn Arrhenius equation , k=AeEaRT , A may be termed as rate constant .
View SolutionRate of a reaction can be expressed by Arrhenius equation as:
k=Ae−Ea/RT
In this equation, Ea represents:
View SolutionIn the Arrhenius equation, k=Aexp−Ea/RT, A may be termed as the rate constant at…………. .
View SolutionThe Arrhenius equation expressing the effect of temperature on the rate constant of a reaction is given as
View SolutionFor a first order reaction A→P, the temperature (T) dependent rate constant (k) was found to follow the equation logk=−2000(1/T)+6.0. The pre-exponential factor A and the activation energy Ea, respective, are
View SolutionThe variation of rate constant with temperature is given by the integrated from of the Arrhenius equation, log10k=−Ea2.303RT + constant
where k = rate cosntant and Ea is the experimental activation energy. If for a certain reaction, log10k=−3163.0T+11.899, calculate Ea.
View SolutionState and explain Arrhenius equation. How can we determine the activation energy of a reaction using this equation?
View SolutionConsider an endothermic reaction X→Y with the activation energies Eb and Ef for the backward and forward reaction, respectively. In general
View Solution