A convex lens is put 10 cm from a light source and it makes a sharp image on a screen, kept 10 cm from the lens. Now a glass block (refractive index 1.5) of 1.5 cm thickness is placed in contact with the light source. To get the sharp image again, the screen is shifted by a distance d. Then d is :
1.1 cm away from the lens
0
0.55 cm towards the lens
0.55 cm away from the lens
To solve the problem step by step, we will analyze the situation involving the convex lens, the light source, and the glass block.
Step 1: Understand the Initial Setup
The convex lens is positioned 10 cm away from a light source, and it forms a sharp image on a screen that is also 10 cm away from the lens. This means that the object distance (u) and the image distance (v) are both 10 cm.
Step 2: Determine the Focal Length of the Lens
Using the lens formula:
1f=1v+1u
Substituting u=−10cm (object distance is taken as negative in lens formula) and v=10cm:
1f=110+1−10=110−110=0
This indicates that the focal length f is 5 cm (since 2f=10).
Step 3: Introduce the Glass Block
Now, a glass block with a refractive index of 1.5 and a thickness of 1.5 cm is placed in contact with the light source. The effective shift in the position of the source due to the glass block can be calculated using the formula:
Shift=t(1−1n)
where t is the thickness of the glass and n is the refractive index.
Step 4: Calculate the Shift
Substituting the values:
Shift=1.5(1−11.5)=1.5(1−23)=1.5×13=0.5cm
This means the effective object distance u is now reduced by 0.5 cm:
u′=10cm−0.5cm=9.5cm
Step 5: Calculate the New Image Distance
Using the lens formula again with the new object distance u′=−9.5cm:
1f=1v′+1u′
Substituting f=5cm:
15=1v′+1−9.5
Rearranging gives:
1v′=15+19.5
Finding a common denominator:
1v′=9.5+55×9.5=14.547.5
Thus,
v′=47.514.5≈3.27cm
Step 6: Calculate the Shift in the Screen Position
The original image distance was 10 cm, and the new image distance is approximately 3.27 cm. The distance d that the screen must be shifted is:
d=v′−10=3.27−10=−6.73cm
Since we are interested in the absolute distance, we take:
d≈6.73cm
Final Answer
The distance d that the screen is shifted is approximately 6.73cm.
The convex lens is positioned 10 cm away from a light source, and it forms a sharp image on a screen that is also 10 cm away from the lens. This means that the object distance (u) and the image distance (v) are both 10 cm.
Using the lens formula:
1f=1v+1u
Substituting u=−10cm (object distance is taken as negative in lens formula) and v=10cm:
1f=110+1−10=110−110=0
This indicates that the focal length f is 5 cm (since 2f=10).
Now, a glass block with a refractive index of 1.5 and a thickness of 1.5 cm is placed in contact with the light source. The effective shift in the position of the source due to the glass block can be calculated using the formula:
Shift=t(1−1n)
where t is the thickness of the glass and n is the refractive index.
Substituting the values:
Shift=1.5(1−11.5)=1.5(1−23)=1.5×13=0.5cm
This means the effective object distance u is now reduced by 0.5 cm:
u′=10cm−0.5cm=9.5cm
Using the lens formula again with the new object distance u′=−9.5cm:
1f=1v′+1u′
Substituting f=5cm:
15=1v′+1−9.5
Rearranging gives:
1v′=15+19.5
Finding a common denominator:
1v′=9.5+55×9.5=14.547.5
Thus,
v′=47.514.5≈3.27cm
The original image distance was 10 cm, and the new image distance is approximately 3.27 cm. The distance d that the screen must be shifted is:
d=v′−10=3.27−10=−6.73cm
Since we are interested in the absolute distance, we take:
d≈6.73cm
The distance d that the screen is shifted is approximately 6.73cm.
Similar Questions
A convex lens has a focal length of 20 cm. It is used to form an image of an object placed 15 cm from lens. The image is
View SolutionA convex lens focusses an object 10 cm from it on a screen placed 10 cm away from it. A glass plate (μ=1.5) of thickenss 1.5 cm is inserted between the lens and the screen. Where should the object be placed so that its image is again focussed on the screen?
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
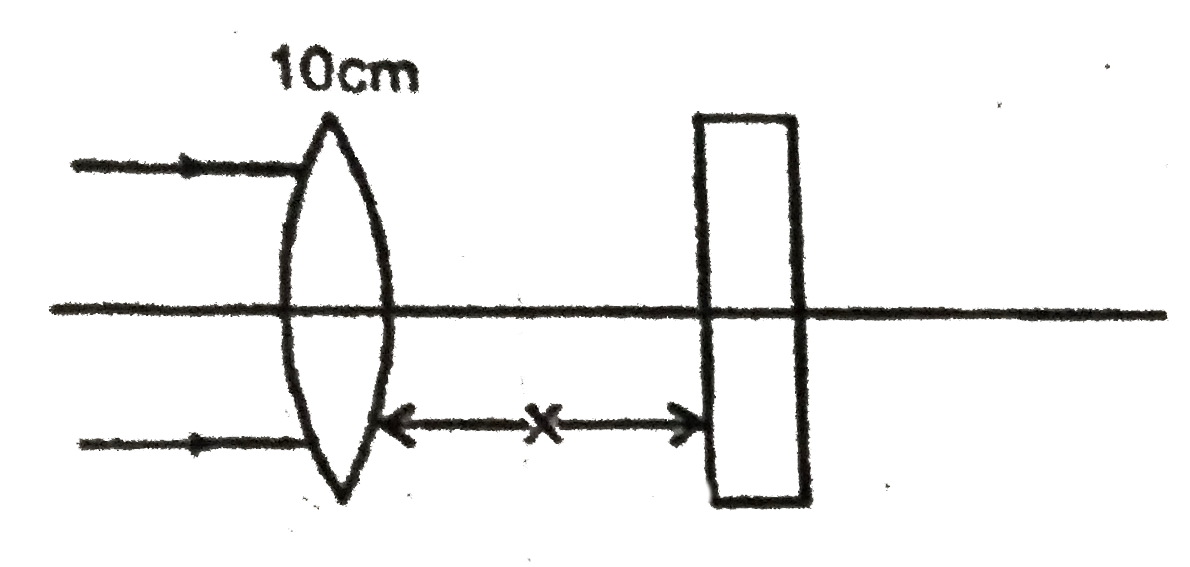
A parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View SolutionAn image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
View SolutionA plano-convex lens of curvature of 30 cm and refractive index 1.5 produces a real image of an object kept 90 cm from it. What is the magnification?
View SolutionA parallel beam of light is incident on a lens of focal length 10cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. The nature of the final image from the lens slab combination is: (Assume rays paraxial)
View SolutionA convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View SolutionAn object is placed 30cm away from a convex lens of focal length 10cm and a sharp image is formed on a screen. Now, a convex lens is placed In contact with the convex lens. The screen now has to be moved by 45cm to get a sharp image again. The magnitude of focal length of the convex lends in (in cm)
View SolutionA thin converging lens of focal length f = 25 cm forms the image of an object on a screen placed at a distance of 75 cm from the lens. Now the screen in moved closer to the lens by a distance of 25 cm. The distance through which the object has to be shifted so that its image on the screen is sharp again is
View Solution
