Two guns A and B can fire bullets at speeds 1 km/s and 2 km/s respectively. From a point on a horizontal ground, they ared fired in all possible directions. The ratio of maximum areas covered by the bullets fired by the two guns, on the ground is :
1:16
1:2
1:4
1:8
To solve the problem of finding the ratio of the maximum areas covered by the bullets fired from two guns A and B, we can follow these steps:
1. Identify the Speeds of the Guns:
- Gun A fires bullets at a speed uA=1km/s.
- Gun B fires bullets at a speed uB=2km/s.
2. Determine the Maximum Range Formula:
- The maximum range Rmax of a projectile is given by the formula:
Rmax=u2g
- Here, u is the initial speed of the projectile and g is the acceleration due to gravity.
3. Calculate the Maximum Range for Each Gun:
- For Gun A:
Rmax,A=u2Ag=(1km/s)2g=1g
- For Gun B:
Rmax,B=u2Bg=(2km/s)2g=4g
4. Calculate the Areas Covered by Each Gun:
- The area covered by the bullets fired from each gun can be modeled as a circle with the radius equal to the maximum range.
- The area A of a circle is given by:
A=πr2
- For Gun A:
AA=π(Rmax,A)2=π(1g)2=πg2
- For Gun B:
AB=π(Rmax,B)2=π(4g)2=16πg2
5. Find the Ratio of the Areas:
- The ratio of the areas covered by the two guns is:
AAAB=πg216πg2=116
6. Final Result:
- Therefore, the ratio of the maximum areas covered by the bullets fired by guns A and B is:
Ratio=1:16
- Gun A fires bullets at a speed uA=1km/s.
- Gun B fires bullets at a speed uB=2km/s.
- The maximum range Rmax of a projectile is given by the formula:
Rmax=u2g
- Here, u is the initial speed of the projectile and g is the acceleration due to gravity.
- For Gun A:
Rmax,A=u2Ag=(1km/s)2g=1g
- For Gun B:
Rmax,B=u2Bg=(2km/s)2g=4g
- The area covered by the bullets fired from each gun can be modeled as a circle with the radius equal to the maximum range.
- The area A of a circle is given by:
A=πr2
- For Gun A:
AA=π(Rmax,A)2=π(1g)2=πg2
- For Gun B:
AB=π(Rmax,B)2=π(4g)2=16πg2
- The ratio of the areas covered by the two guns is:
AAAB=πg216πg2=116
- Therefore, the ratio of the maximum areas covered by the bullets fired by guns A and B is:
Ratio=1:16
Topper's Solved these Questions
Similar Questions
A gun is firing bullets with velocity v0 by rotating it through 360∘ in the horizontal plane. The maximum area covered by the bullets is
View SolutionA large number of bullets are fired in all directions with the same speed v. Find the maximum area on the ground on which these bullets will spread.
View Solution
Knowledge Check
- Question 1 - Select One
A gun fires two bullets at 60∘ and 30∘ with horizontal. The bullets strike at same horizontal distance. The ratio of the maximum height for the two bullets is in the ratio
A2:1B3:1C4:1D1:1 - Question 2 - Select One
A large number of bullets are fired in all directions with the 'same speed v∘. The maximum area on the ground on which these bullets will spread is
Aπv2gBπv4g2Cπ2v2g2Dπ2v4g2
A particle is fired from a point on the ground with speed u making an angle θ with the horizontal.Then
View SolutionA number of bullets are fired horizontally with different velocities from the top of a tower they reach the ground
View Solution(A) : When bullet is fired from a gun, the gunner should exert force on gun in the direction of motion of bullet.
(R) : The gun recoils when bullet is fired.View SolutionTwo bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit the ground first?
View Solution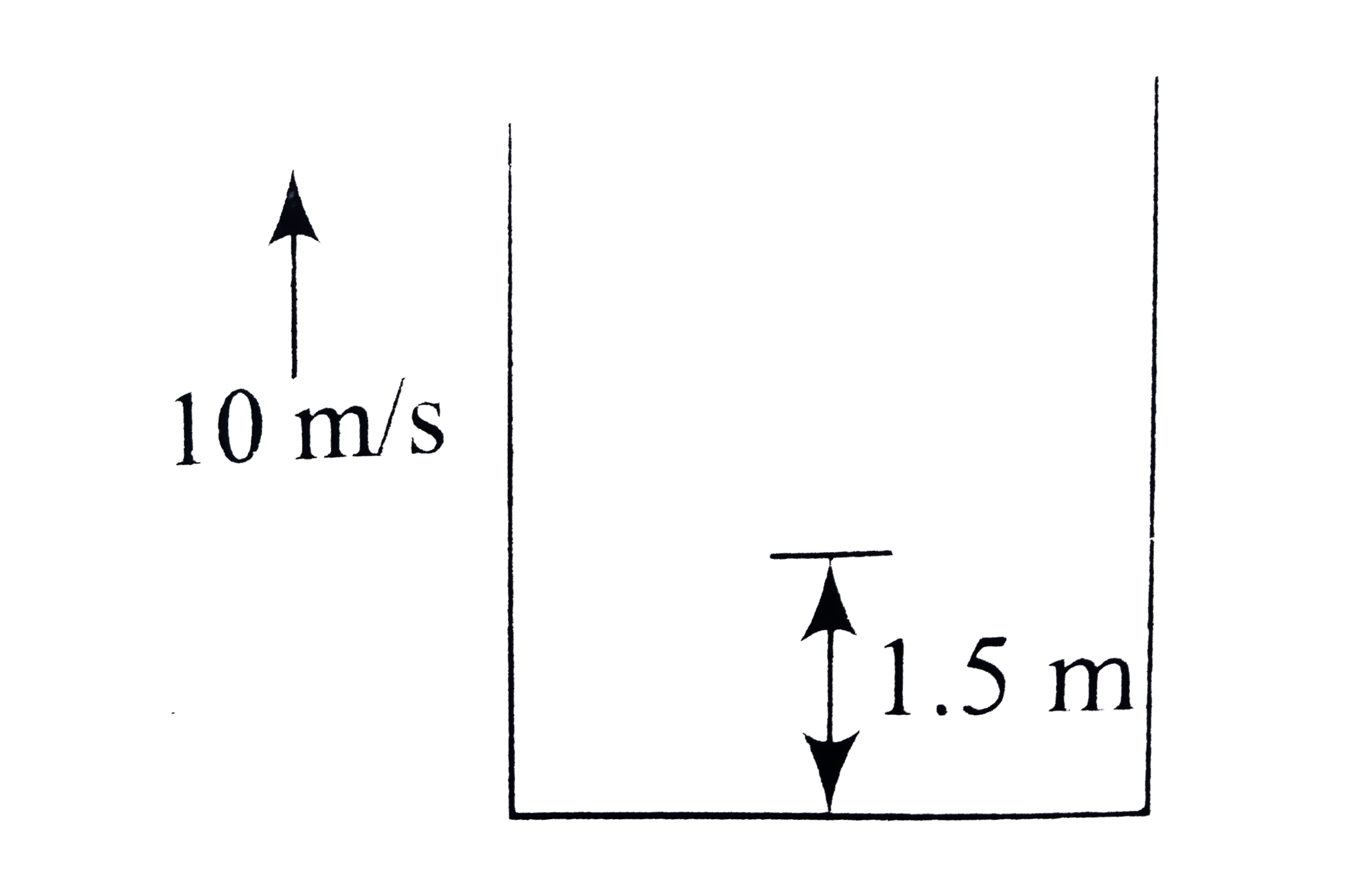
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :View SolutionA machine gun fires bullets of 50gm at the speed of 1000m/sec. If an average force of 200N is exerted on the gun, the maximum number of bullets fired per minute is:
View Solution

