A solid metal cube of edge length 2 cm is moving in a positive y-direction at a constant speed of 6 m/s. There is a uniform magnetic field of 0.1 T in the positive z-direction. The potential difference between the two faces of the cube perpendicular to the x-axis, is :
12 mV
6 mV
1 mV
2 mV
To find the potential difference between the two faces of the cube that are perpendicular to the x-axis, we can use the formula for induced electromotive force (emf) in a conductor moving through a magnetic field. The formula is given by:
emf=B⋅v⋅l
where:
- B is the magnetic field strength,
- v is the velocity of the conductor,
- l is the length of the conductor in the direction perpendicular to both the magnetic field and the velocity.
Step 1: Identify the parameters.
- The edge length of the cube is given as 2cm=0.02m.
- The velocity v of the cube is 6m/s.
- The magnetic field B is 0.1T.
Step 2: Determine the length l that is perpendicular to both the magnetic field and the velocity.
- In this case, the length l is the edge length of the cube that is perpendicular to the direction of motion (y-direction) and the magnetic field (z-direction). Thus, l=0.02m.
Step 3: Substitute the values into the formula.
emf=B⋅v⋅l=0.1T⋅6m/s⋅0.02m
Step 4: Calculate the induced emf.
emf=0.1⋅6⋅0.02=0.012V=12mV
Thus, the potential difference between the two faces of the cube perpendicular to the x-axis is 12 mV.
- B is the magnetic field strength,
- v is the velocity of the conductor,
- l is the length of the conductor in the direction perpendicular to both the magnetic field and the velocity.
- The edge length of the cube is given as 2cm=0.02m.
- The velocity v of the cube is 6m/s.
- The magnetic field B is 0.1T.
- In this case, the length l is the edge length of the cube that is perpendicular to the direction of motion (y-direction) and the magnetic field (z-direction). Thus, l=0.02m.
emf=B⋅v⋅l=0.1T⋅6m/s⋅0.02m
emf=0.1⋅6⋅0.02=0.012V=12mV
Topper's Solved these Questions
Similar Questions
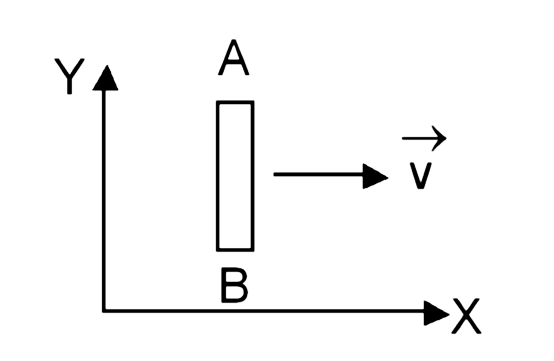
A conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-
View SolutionConsider the following figure, a uniform magnetic field of 0.2 T is directed along the positive X-axis. The magnetic flux through top surface of the figure.
View Solution
Knowledge Check
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
A metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
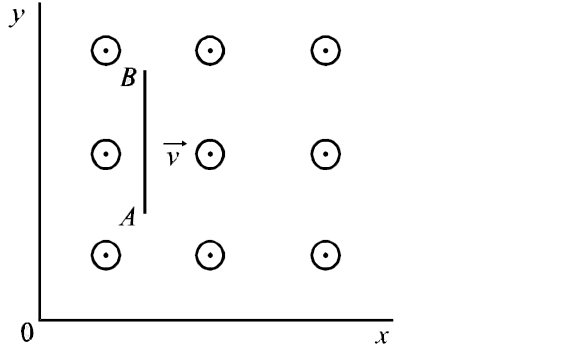
View SolutionA conducting rod AB moves parallel to the x-axis (see Fig.) in a uniform magnetic field pointing in the positive z-direction. The end A of the rod gets positively charged.
 .
.
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
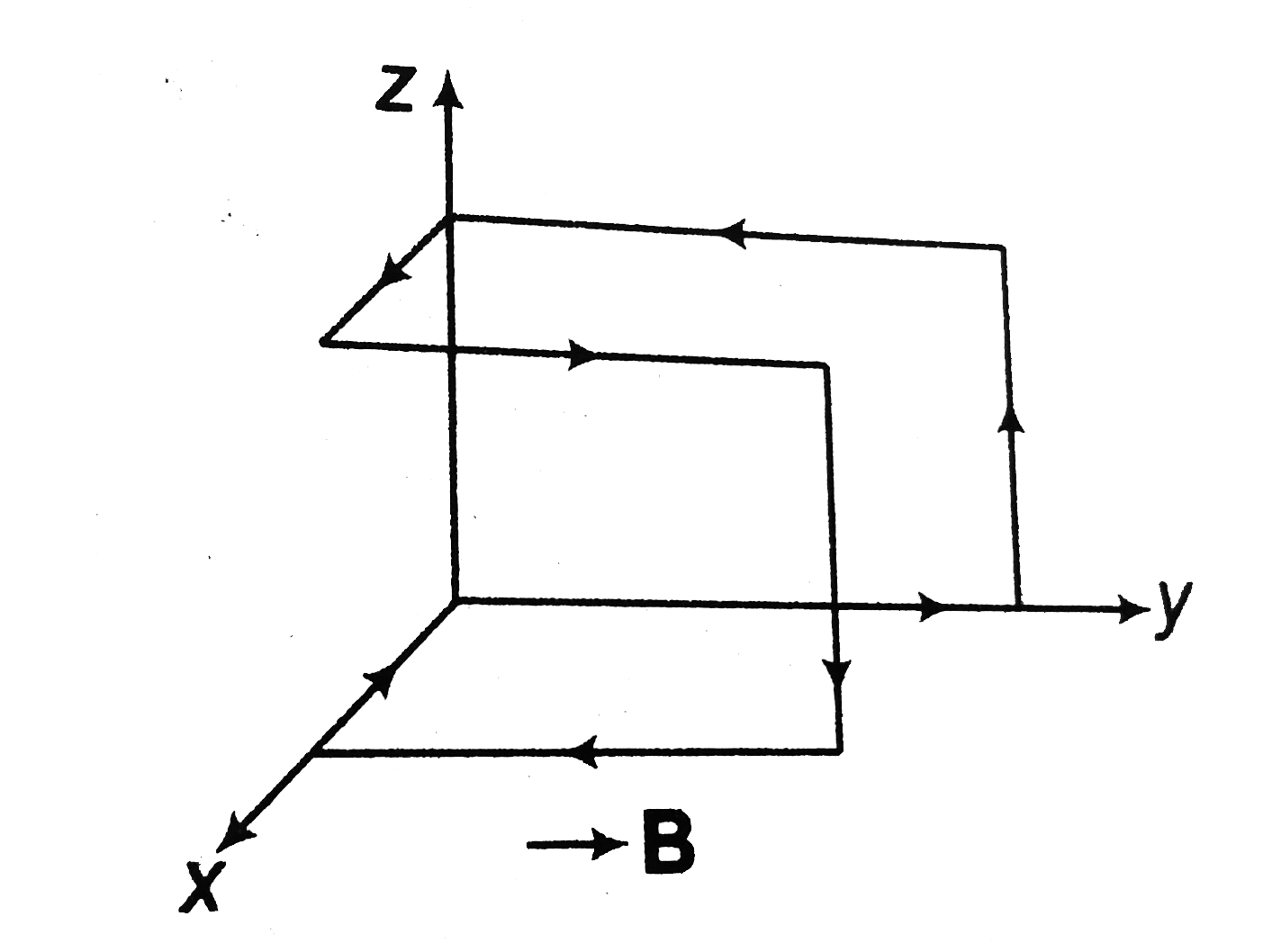
View SolutionGiven figure shows a coil bent with all edges of length 1m and carrying a current of 1A. There exists in space a uniform magnetic field of 2T in positive y-direction. Find the torque on the loop.
View SolutionA proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
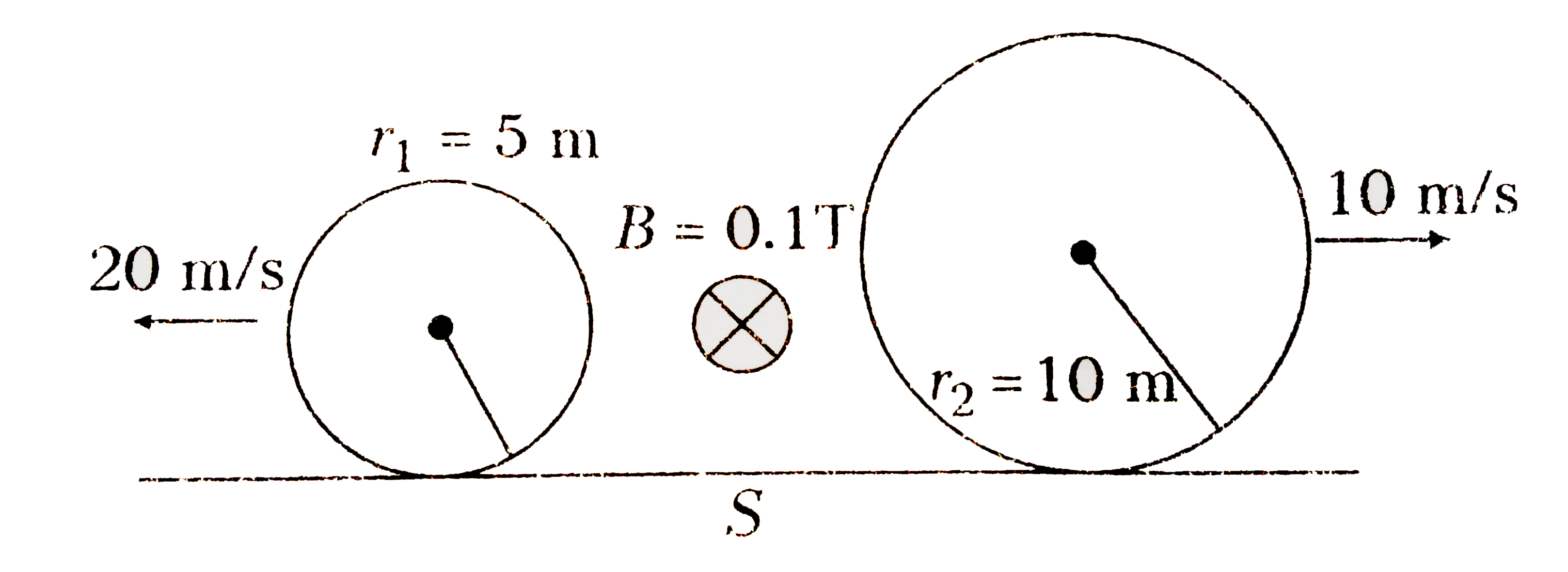
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
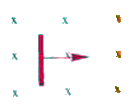
View Solution
