The Wheatstone bridge shown in Fig. here, gets balanced when the carbon resistor used as R1 has the colour code (Orange, Red, Brown). The resistors R2andR4 are 80Ω and 40Ω, respectively.
Assuming that the colour code for the carbon resistor, used as R3, would be:

Brown, Blue, Brown
Brown, Green, Black
Red, Green, Brown
Grey, Black, Brown
Step by step video & image solution for The Wheatstone bridge shown in Fig. here, gets balanced when the carbon resistor used as R_(1) has the colour code (Orange, Red, Brown). The resistors R_(2) and R_(4) are 80 Omega and 40 Omega, respectively. Assuming that the colour code for the carbon resistor, used as R_(3), would be: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A cell of e.m.f. 2V and negligible internal resistance is connected to resistor R1 and R2 as shown in the figure. The resistance of the Voltmeter R1 and R2 are 80Ω,40Ω and 80Ω respectively. The reading of the voltmeter is:-
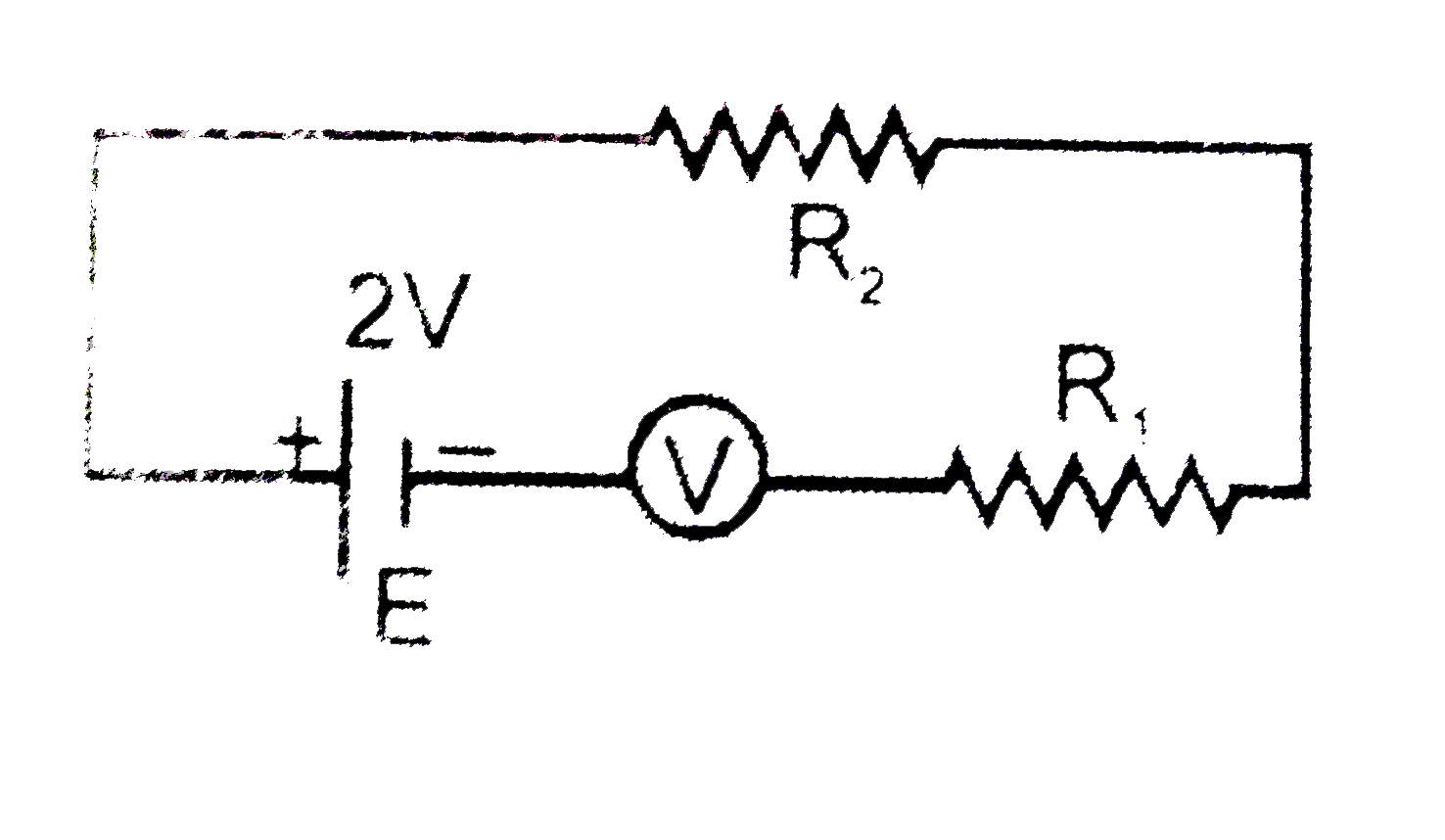
View SolutionWhat is the colour code of a carbon resistor having a resistance of 470Ω and a tolerance of 5% ?
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
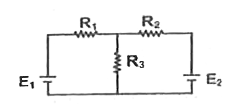
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3

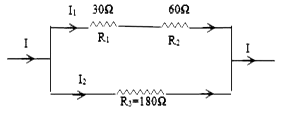
View SolutionIn Figure below, power developed in resistor R1 is 120W. Find the power developed in resistor R3.
View SolutionThe resistance of a carbon resistor of colour code Red-Red Green Silver is (in kΩ)
View SolutionDetermine the voltage drop across the resistor R1 in the circuit given below with E=65V,R1=50Ω,R2=100Ω,R3=100Ω and R4300Ω

View SolutionTwo resistor R1=(24±0.5)ΩandR2=(8±0.3)Ωare joined in series, The equivalent resistence is
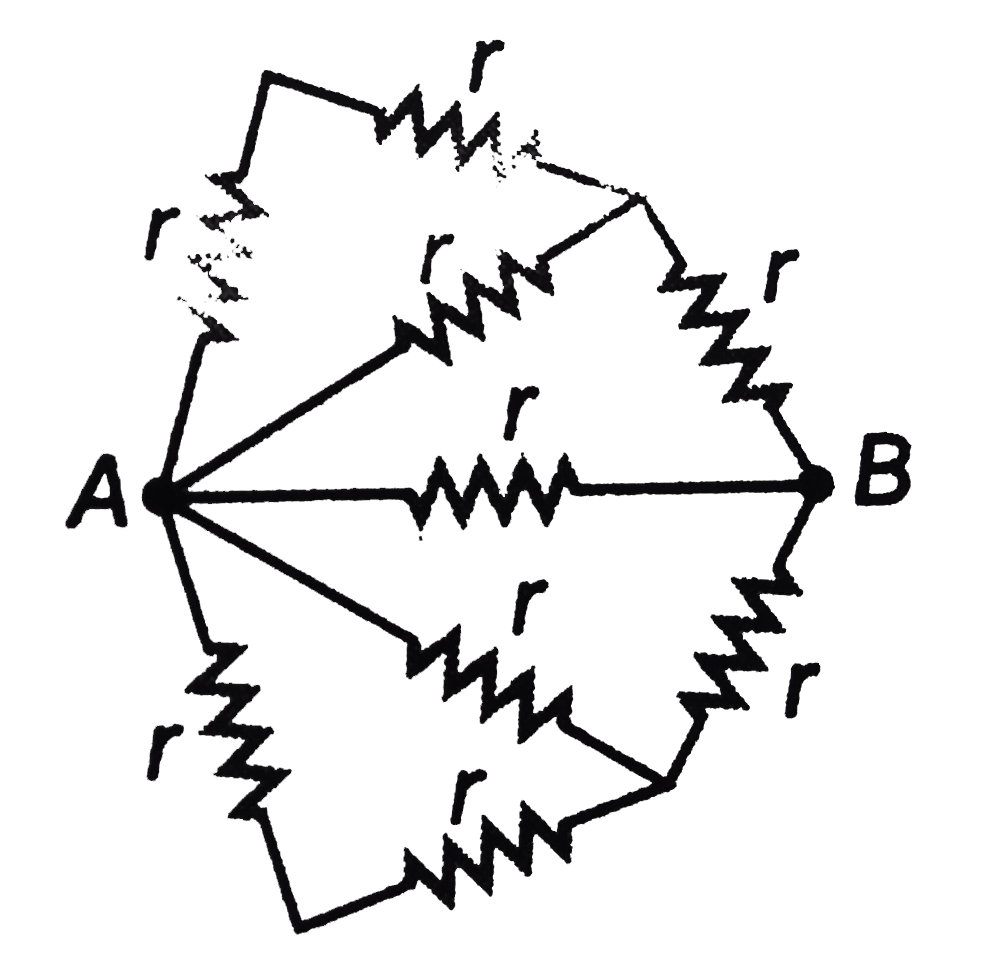
View SolutionThe network shown in figure is an arrangement of nine identical resistors. The resistance of the network between points A and B is 1.5Ω. The resistance r is
View SolutionA 2 W carbon resistor is color coded with green, black, red and brown respectively. The maximum current which can be passed through this resistor is :
View Solution
