An object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of the speed and direction of the image will be :
away from the lens
away from the lens
towards the lens
towards the lens
To solve the problem step by step, we will use the lens formula and the concept of magnification.
Step 1: Identify the given values
- Focal length of the convex lens (f) = 0.3 m
- Object distance (u) = -20 m (negative because it is on the same side as the incoming light)
- Speed of the object moving away from the lens = 5 m/s
Step 2: Use the lens formula
The lens formula is given by:
1f=1v−1u
Rearranging this, we can express 1v as:
1v=1f+1u
Step 3: Substitute the values into the lens formula
Substituting f=0.3 m and u=−20 m:
1v=10.3+1−20
Calculating 10.3 and 1−20:
10.3=103,1−20=−120
Finding a common denominator (60):
1v=10×2060−360=200−360=19760
Thus,
v=60197 m
Step 4: Calculate the magnification (m)
The magnification (m) is given by:
m=vu
Substituting the values of v and u:
m=60197−20=−603940=−3197
Step 5: Calculate the velocity of the image (v_i)
The velocity of the image with respect to the lens can be calculated using the formula:
vi=m⋅vo
Where vo is the velocity of the object (5 m/s):
vi=−3197⋅5=−15197 m/s
Step 6: Determine the direction of the image
Since the velocity of the image is negative, it means the image is moving towards the lens.
Final Result
The speed of the image is approximately 0.076 m/s (or 7.6×10−2 m/s), and it is moving towards the lens.
---
- Focal length of the convex lens (f) = 0.3 m
- Object distance (u) = -20 m (negative because it is on the same side as the incoming light)
- Speed of the object moving away from the lens = 5 m/s
The lens formula is given by:
1f=1v−1u
Rearranging this, we can express 1v as:
1v=1f+1u
Substituting f=0.3 m and u=−20 m:
1v=10.3+1−20
Calculating 10.3 and 1−20:
10.3=103,1−20=−120
Finding a common denominator (60):
1v=10×2060−360=200−360=19760
Thus,
v=60197 m
The magnification (m) is given by:
m=vu
Substituting the values of v and u:
m=60197−20=−603940=−3197
The velocity of the image with respect to the lens can be calculated using the formula:
vi=m⋅vo
Where vo is the velocity of the object (5 m/s):
vi=−3197⋅5=−15197 m/s
Since the velocity of the image is negative, it means the image is moving towards the lens.
The speed of the image is approximately 0.076 m/s (or 7.6×10−2 m/s), and it is moving towards the lens.
Topper's Solved these Questions
Similar Questions
An object is put at a distance of 5cm from the first focus of a convex lens of focal length 10cm. If a real image is formed, its distance from the lens will be
View SolutionAn object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionA point object O approaches a biconvex lens of focal length 40 cm along its optic axis with a speed of 10 m/s while the later receeds away from the former with a speed of 4 cm/s. Find the speed and direction of motion of the image when the object is at a distance of 60 cm from the lens.

View SolutionA convex lens has a focal length of 20 cm. It is used to form an image of an object placed 15 cm from lens. The image is
View SolutionA point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2 m. It is then cut into two halves each of which is displaced by 0.0005 m as shown in figure.
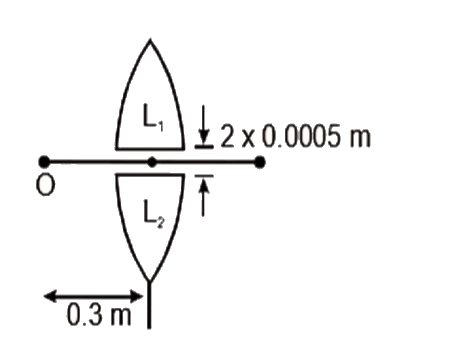
image will be formed from the lens at a distance of
View SolutionA point like object is placed at a distance of 1 m in front of a convex lens of focal length 0.5 m . A plane mirror is placed at a distance of 2 m behind the lens. The position and nature of the final image formed by the system is :
View Solution
A point object is placed at a distance of 0.3 m from a convex lens (focal length 0.2 m) cut into two halves each of which is displaced by 0.0005 m as shown in the figure. Find the position of the image . If more than one image is formed find their number and the distance between them.
View Solution
A point object is placed at a distance of 0.3 m from a convex lens (focal length 0.2 m) cut into two halves each of which is displaced by 0.0005 m as shown in the figure. Find the position of the image . If more than one image is formed find their number and the distance between them.
View Solution
A point object is placed at a distance of 0.3 m from a convex lens (focal length 0.2 m) cut into two halves each of which is displaced by 0.0005 m as shown in the figure. Find the position of the image . If more than one image is formed find their number and the distance between them.
View Solution
