In an experiment ,electrons are accelerated from rest, by applying a voltage of 500 V.Calculate the radius of the path if a magnetic field 100 m T is then applied .Charge of the electron =1.6×10−19C
Mass of the electron =9.1×10−31 Kgl
7.5×103m
7.5×102m
7.5 m
7.5×10−4m
To solve the problem, we need to calculate the radius of the path of electrons accelerated by a voltage of 500 V in a magnetic field of 100 mT. We will use the relationship between the centripetal force and the magnetic force acting on the electrons.
1. Understanding the Forces:
The centripetal force acting on the electron moving in a circular path is provided by the magnetic force. The centripetal force can be expressed as:
Fc=mv2R
where m is the mass of the electron, v is its velocity, and R is the radius of the path.
The magnetic force acting on the electron is given by:
Fm=qvB
where q is the charge of the electron and B is the magnetic field strength.
2. Setting the Forces Equal:
Since the centripetal force is provided by the magnetic force, we can set these two forces equal:
mv2R=qvB
3. Rearranging for Radius R:
Rearranging the equation gives:
R=mvqB
4. Finding the Velocity v:
The velocity of the electron can be found using the kinetic energy gained from the applied voltage. The kinetic energy KE is given by:
KE=qV
where V is the voltage. The kinetic energy can also be expressed as:
KE=12mv2
Setting these equal gives:
12mv2=qV
Solving for v:
v=√2qVm
5. Substituting v into the Radius Formula:
Now we substitute v back into the radius formula:
R=m√2qVmqB
Simplifying this gives:
R=√2mqVqB
6. Substituting Values:
Now we can substitute the known values:
- m=9.1×10−31kg
- q=1.6×10−19C
- V=500V
- B=100mT=100×10−3T
Plugging in these values:
R=√2×(9.1×10−31)×(1.6×10−19)×500(1.6×10−19)×(100×10−3)
7. Calculating the Radius:
First calculate the numerator:
2×(9.1×10−31)×(1.6×10−19)×500=7.28×10−16
Taking the square root gives:
√7.28×10−16≈8.54×10−8
Now calculate the denominator:
(1.6×10−19)×(100×10−3)=1.6×10−21
Finally, calculate R:
R=8.54×10−81.6×10−21≈5.34×1013m
Final Result:
The radius of the path of the electrons is approximately:
R≈7.54×10−4mor0.754mm
The centripetal force acting on the electron moving in a circular path is provided by the magnetic force. The centripetal force can be expressed as:
Fc=mv2R
where m is the mass of the electron, v is its velocity, and R is the radius of the path.
Fm=qvB
where q is the charge of the electron and B is the magnetic field strength.
Since the centripetal force is provided by the magnetic force, we can set these two forces equal:
mv2R=qvB
Rearranging the equation gives:
R=mvqB
The velocity of the electron can be found using the kinetic energy gained from the applied voltage. The kinetic energy KE is given by:
KE=qV
where V is the voltage. The kinetic energy can also be expressed as:
KE=12mv2
Setting these equal gives:
12mv2=qV
Solving for v:
v=√2qVm
Now we substitute v back into the radius formula:
R=m√2qVmqB
Simplifying this gives:
R=√2mqVqB
Now we can substitute the known values:
- m=9.1×10−31kg
- q=1.6×10−19C
- V=500V
- B=100mT=100×10−3T
R=√2×(9.1×10−31)×(1.6×10−19)×500(1.6×10−19)×(100×10−3)
First calculate the numerator:
2×(9.1×10−31)×(1.6×10−19)×500=7.28×10−16
Taking the square root gives:
√7.28×10−16≈8.54×10−8
(1.6×10−19)×(100×10−3)=1.6×10−21
R=8.54×10−81.6×10−21≈5.34×1013m
The radius of the path of the electrons is approximately:
R≈7.54×10−4mor0.754mm
Topper's Solved these Questions
Similar Questions
Knowledge Check
An electron of energy 1800 eV describes a circular path in magnetic field of flux density 0.4 T. The radius of path is (q=1.6×10−19C,me=9.1×10−31kg)
A2.58×10−4mB3.58×10−4mC2.58×10−3mD3.58×10−4m
Molar mass of electron is nearly : (NA=6×1023),
mass of e− = 9.1 ×10−31Kg
View SolutionCalculate the uncertainty in the position (Δx) of an electron if Δvis0.1% .Take the velocity of electron =2.2×106ms−1 and mass of electron as 9.108×10−31kg
View SolutionCalculate the product of the uncertainty of the displacement and velocity of a electron having mass 9.1×10−28g
View SolutionSuppose the an electron in the picture tube of a televisoin set is accelerated from rest through a potential differnece Vb−Va=Vba=+5000V.
(a) What is the change in electric potential energy of the electron?
(b) What is the speed of the electron (m=9.1×10−31kg) as a result of this acceleration ?
View SolutionAn electron moving along the x-axis with an initial energy of 100eV enters a region of magnetic field →B=(1.5×10−3T)ˆk at S (see figure). The field extends between x=0 and x=2cm. The electron is detected at the point Q on a screen placed 8 cm away from the point S. The distance d between P and Q (on the screen) is :
(electron's charge =1.6×10−19C, mass of electron =9.1×10−31kg).
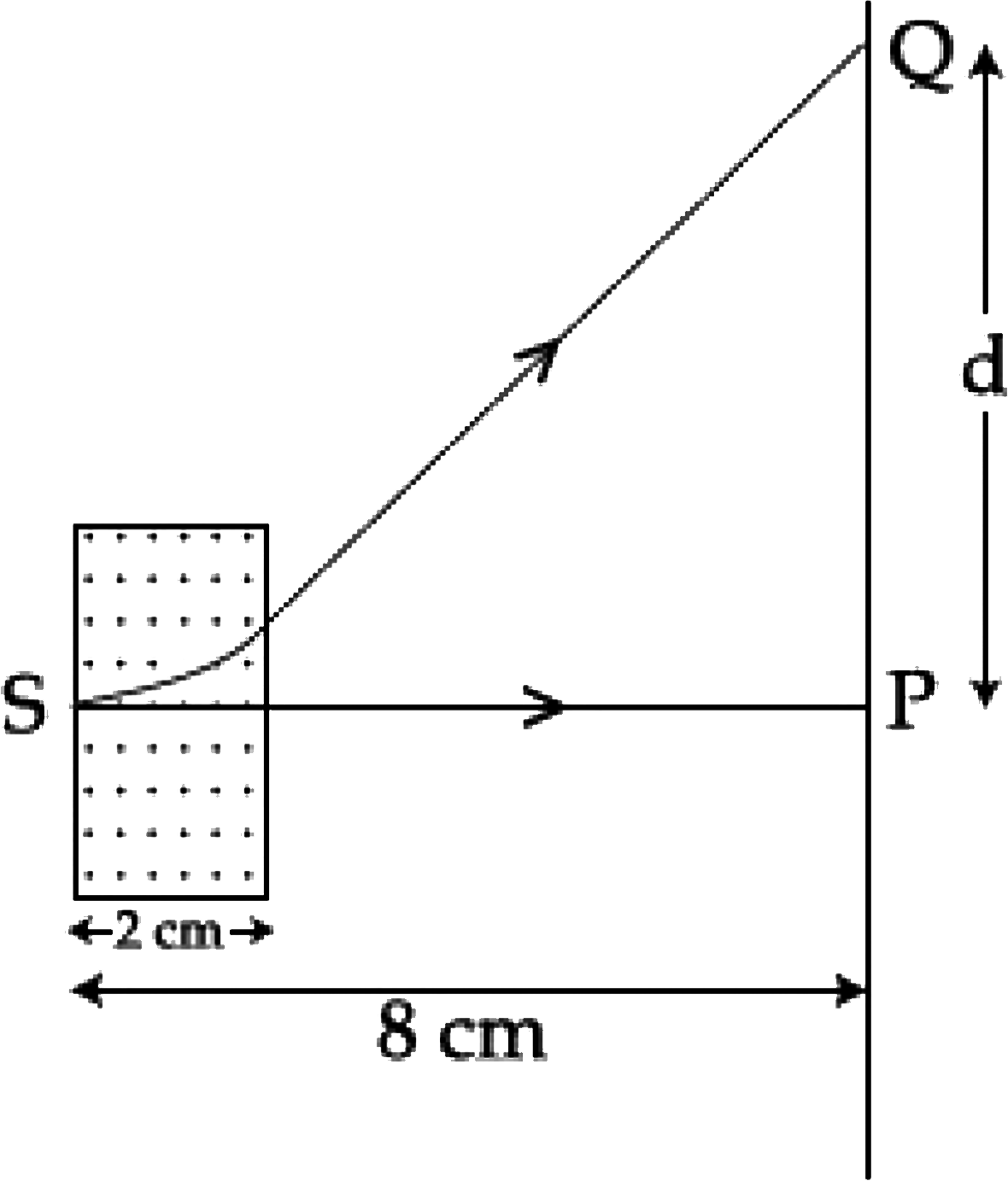 a) 11.65cm. b) 12.87 cm
c) 1.22cm
d) 2.25cm
a) 11.65cm. b) 12.87 cm
c) 1.22cm
d) 2.25cm
View SolutionAn electron accelerated through 500 V , enters a transverse uniform magnetic field of magnitude 100 mT . The radius of the circular path described by the electron is nearly
View SolutionThe kinetic energy of an electron is 4.55×10−25J .The mass of electron is 9.1×10−34kg. Calculate velocity of the electron.
View Solution
