A person standing on an open ground hears the sound of a jet aeroplane , coming from north at an angle 60∘ with ground level ,But he finds the aeroplane right vertically above his position , if V is the speed of sound , speed of the plane is :
√32v
2v√3
v
v2
To solve the problem, we need to analyze the situation described. We have a person on the ground who hears the sound of a jet airplane coming from the north at an angle of 60 degrees with the ground level. However, the airplane appears to be directly above him. We need to find the speed of the airplane in terms of the speed of sound, denoted as V.
1. Understanding the Geometry:
- The airplane is coming from the north at an angle of 60∘ with respect to the ground.
- The horizontal component of the airplane's motion can be represented as dcos(60∘), where d is the distance the airplane has traveled vertically.
2. Components of Motion:
- The vertical distance traveled by the airplane is d.
- The horizontal distance traveled by the airplane is dcos(60∘).
- Since cos(60∘)=12, the horizontal distance becomes d2.
3. Time of Travel:
- Let vp be the speed of the airplane. The time taken for the airplane to travel the horizontal distance is given by:
t=Horizontal DistanceSpeed of Plane=d2vp
4. Sound Travel Time:
- The time taken for the sound to travel the vertical distance d is given by:
t=dV
- Here, V is the speed of sound.
5. Setting the Times Equal:
- Since both the airplane and the sound reach the observer at the same time, we can set the two expressions for time equal to each other:
d2vp=dV
6. Cancelling d:
- We can cancel d from both sides (assuming d≠0):
12vp=1V
7. Solving for vp:
- Rearranging gives:
2vp=V⇒vp=V2
Final Answer:
The speed of the airplane is:
vp=V2
- The airplane is coming from the north at an angle of 60∘ with respect to the ground.
- The horizontal component of the airplane's motion can be represented as dcos(60∘), where d is the distance the airplane has traveled vertically.
- The vertical distance traveled by the airplane is d.
- The horizontal distance traveled by the airplane is dcos(60∘).
- Since cos(60∘)=12, the horizontal distance becomes d2.
- Let vp be the speed of the airplane. The time taken for the airplane to travel the horizontal distance is given by:
t=Horizontal DistanceSpeed of Plane=d2vp
- The time taken for the sound to travel the vertical distance d is given by:
t=dV
- Here, V is the speed of sound.
- Since both the airplane and the sound reach the observer at the same time, we can set the two expressions for time equal to each other:
d2vp=dV
- We can cancel d from both sides (assuming d≠0):
12vp=1V
- Rearranging gives:
2vp=V⇒vp=V2
The speed of the airplane is:
vp=V2
Topper's Solved these Questions
Similar Questions

A stone projected at an angle of 60∘ from the ground level strikes at an angle of 30∘ on the roof of a building of height h. Then the speed of projection of the stone is:
View Solution
A stone projected at an angle of 60∘ from the ground level strikes at an angle of 30∘ on the roof of a building of height h. Then the speed of projection of the stone is:
View SolutionA man standing on a platform hears the sound of frequency 604 Hz coming from a frequency 550 Hz from a train whistle moving towards the platform. If the velocity of sound is 330 m/s, then what is the speed of train?
View SolutionThe angle of elevation of an aeroplane from a point P on the ground is 60∘. After a flight of 15 seconds, the angle of elevation changes to 30∘. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the aeroplane
View SolutionThe angle of elevation of an aeroplane from a point on the ground is 45∘ . After a flight of 15 seconds, the elevation changes to 30∘ . If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
View SolutionThe angle of elevation of a jet plane from a point A on the ground is 60o . After a flight of 30 seconds, the angle of elevation changes to 30o . If the jet plane is flying at a constant height of 3600√3m , find the speed of the jet plane.
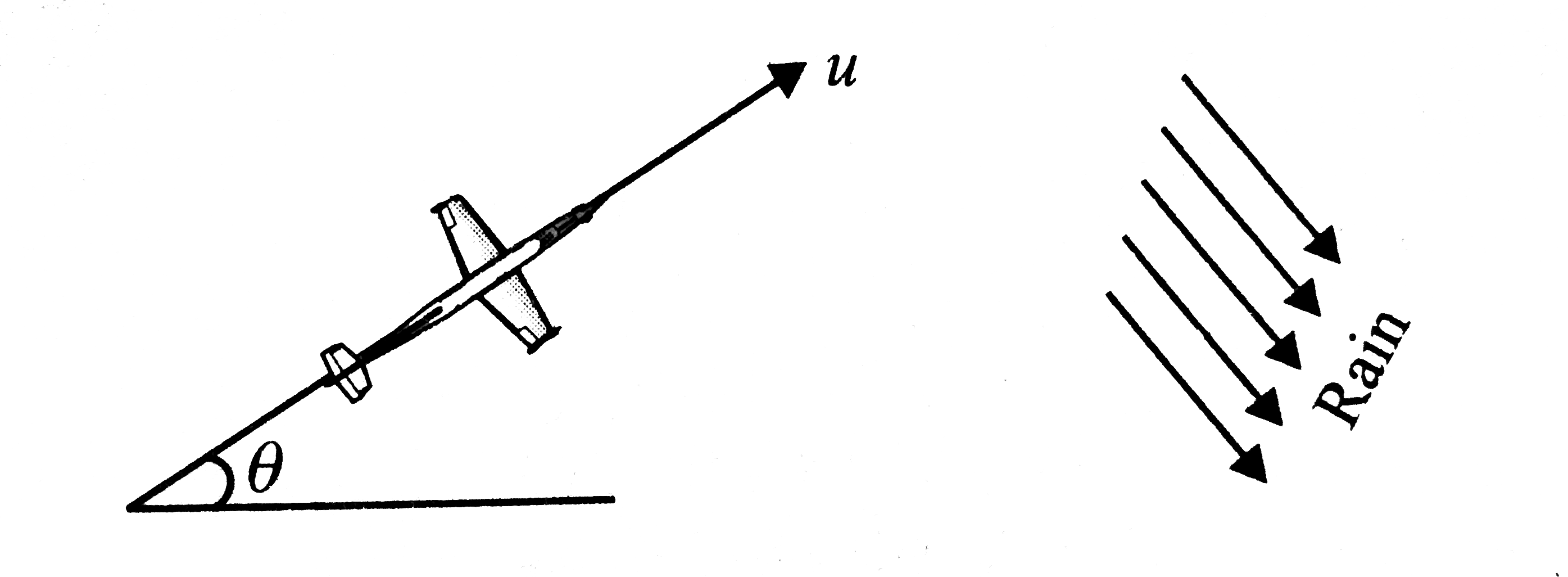
View SolutionRain is falling with a sped of 12√2m/s at an angle 45∘ with the vertical line. A man in a glider going at a speed of u at an angle of 37∘ with respect to the ground. Find the speed of the glider so that rain appears to him falling vertically. Consider the motion of the glider and rain drops in the same vertical plane.
View SolutionAn aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60o . After 10 seconds, its elevation is observed to be 30o . Find the speed of the aeroplane in km/hr.
View SolutionThe angle of elevation of an aeroplane from a point P on the ground is 60∘. After 12 seconds from the same point P, the angle of elevation of the same plane changes to 30∘. If the plane is flying horizontally at a speed of 600√3 km/h, find the height at which the plane is flying.
View SolutionA person standing near the edge of the top of a building throws two balls A and B. The ball A is thrown vertically upward and B is thrown vertically downward with the same speed. The ball A hits the ground with speed vA and the ball B hits the ground wiht a speed vB. We have
View Solution
