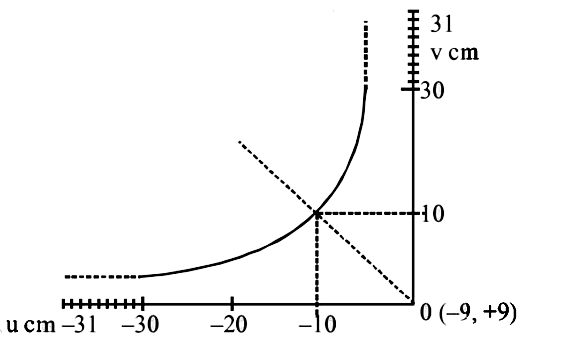
In an optics experiment, with the position of the object fixed, a student varies the position of a convex lens and for each position, the screen is adjusted to get a clear image of the object. A graph between the object distance u and the image distance v, from the lens, is plitted using the same scale for the two axes. A straight line passing through the origin and making an angle of 45∘ with x-axis meets the experimental curve at P. The coordinates of P will be.
(2f,2f)
(f2,f2)
(f, f)
(4f, 4f)
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the object distance (u) and the image distance (v) for a convex lens, and how they relate to the straight line that makes a 45-degree angle with the x-axis.
1. Understanding the Lens Formula:
The lens formula for a convex lens is given by:
1f=1v−1u
where f is the focal length of the lens, v is the image distance, and u is the object distance.
2. Setting Up the Graph:
We are plotting a graph with object distance u on the x-axis (which is negative for real objects) and image distance v on the y-axis. The line that makes a 45-degree angle with the x-axis has a slope of 1, meaning:
v=−u
(since u is negative, we take the absolute value).
3. Finding the Intersection Point:
The line v=−u intersects the experimental curve at point P. At this point, we have:
|v|=|u|
This means that the magnitudes of u and v are equal.
4. Substituting into the Lens Formula:
Since |v|=|u|, we can substitute v=−u into the lens formula:
1f=1−u−1u
This simplifies to:
1f=−1u−1u=−2u
Rearranging gives:
u=−2f
Since v=−u, we also have:
v=2f
5. Coordinates of Point P:
The coordinates of point P, where the line intersects the curve, are:
(u,v)=(−2f,2f)
Final Answer:
The coordinates of point P are:
(−2f,2f)
The lens formula for a convex lens is given by:
1f=1v−1u
where f is the focal length of the lens, v is the image distance, and u is the object distance.
We are plotting a graph with object distance u on the x-axis (which is negative for real objects) and image distance v on the y-axis. The line that makes a 45-degree angle with the x-axis has a slope of 1, meaning:
v=−u
(since u is negative, we take the absolute value).
The line v=−u intersects the experimental curve at point P. At this point, we have:
|v|=|u|
This means that the magnitudes of u and v are equal.
Since |v|=|u|, we can substitute v=−u into the lens formula:
1f=1−u−1u
This simplifies to:
1f=−1u−1u=−2u
Rearranging gives:
u=−2f
Since v=−u, we also have:
v=2f
The coordinates of point P, where the line intersects the curve, are:
(u,v)=(−2f,2f)
The coordinates of point P are:
(−2f,2f)
Topper's Solved these Questions
Similar Questions
 .
.
The graph between object distance u and image distance v from a convex lens is given .The correct option option , from the following ,is
View SolutionA convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View SolutionThe graph shown relationship between object distance and image distance for a equiconvex lens. Then focal length of the lens is
View SolutionThe object distance u, the image distance v and the magnification m in a lens follow certain linear relations.
View SolutionAn object is placed 12cm in front of a lens to form an image on a screen. The size of the image is twice that of the object. What is the distance between the object and the image?
View SolutionState the position of the object in front of a converging lens if :
It produces a real and same size image of the object.
View SolutionA convex lens produces a real image m times the size of the object. What will be the distance of the object from the lens ?
View SolutionAn object is placed at a distance of f/2 from a convex lens. The image will be
View SolutionAn extended real object is placed perpendicular to the principle axis of a concave of focal length 10cm, such that the images found is half the size of object
(a) Find the object distance from the lines
(b) Find the image distance from the lens
View SolutionIn an experiment for finding the focal length of a thin convex lens using two - pin method the position of the image .υ. is recorded for various positrons .u. of the object. Which of the following best represents object distance u versus image distance υ−graph.
View Solution
