Consider a rubber ball freely falling from a height onto a horizontally elastic plate. Assume that the duration of collision is negligible and the collisions with the plate is totally elastic .
Then the velocity as a function of time and the height as a function of time will be :
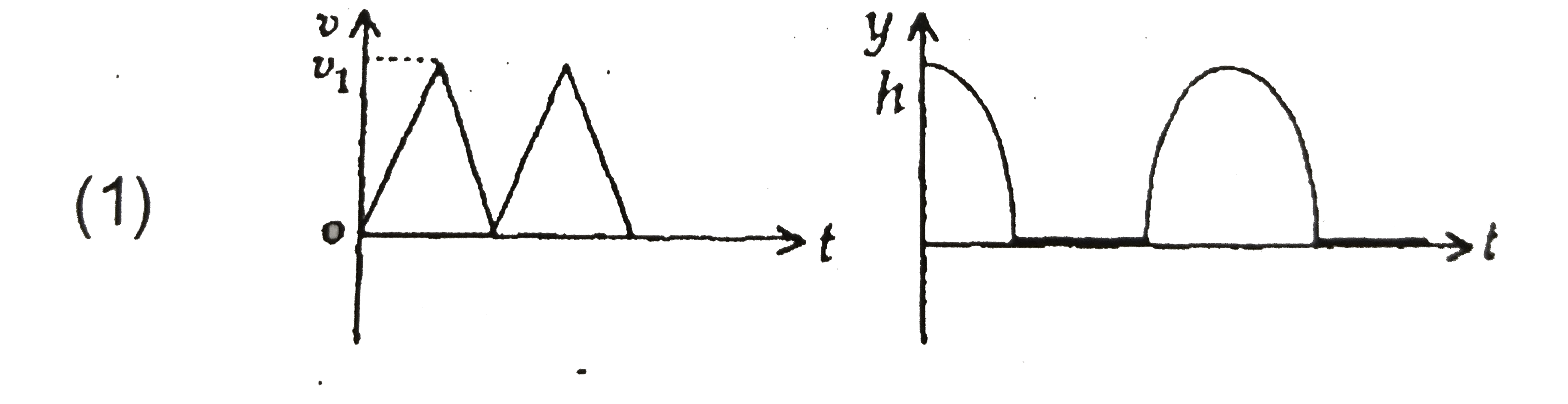
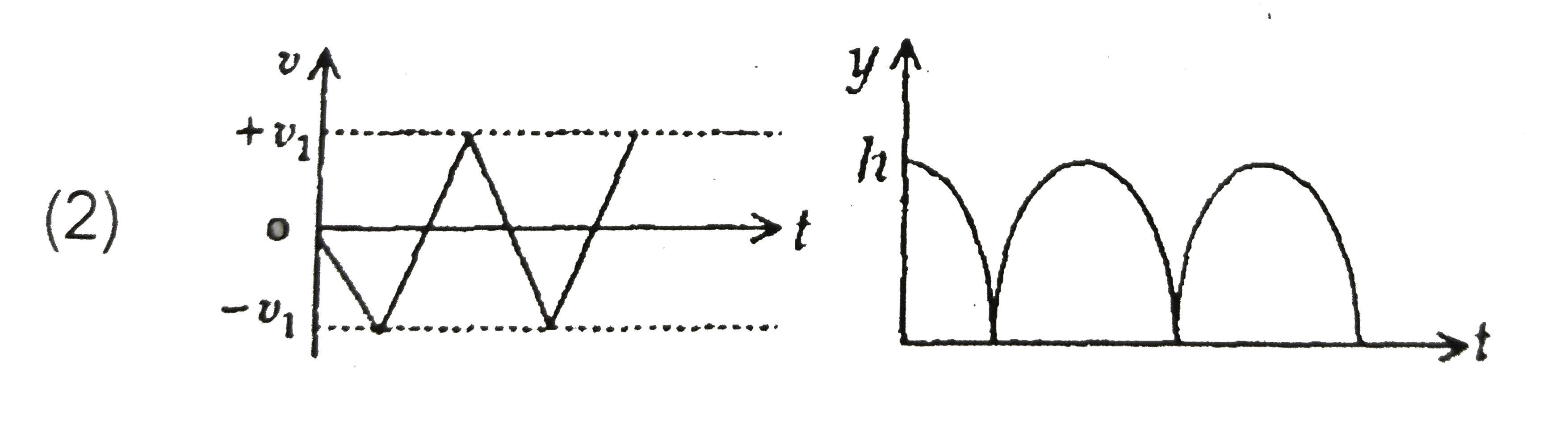
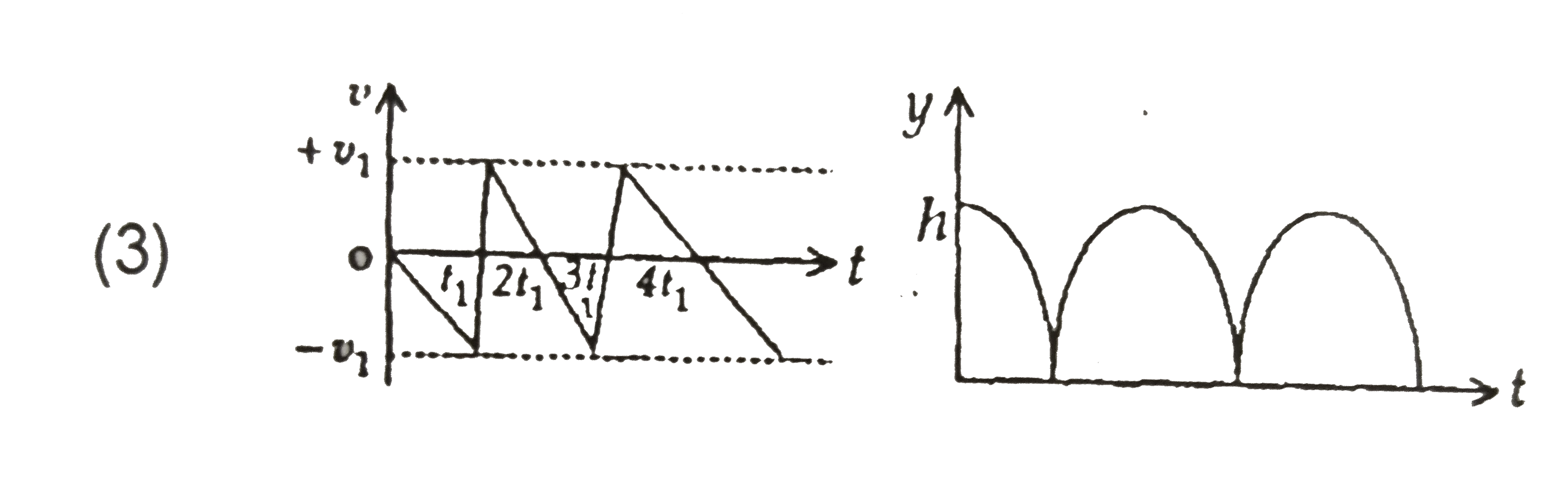
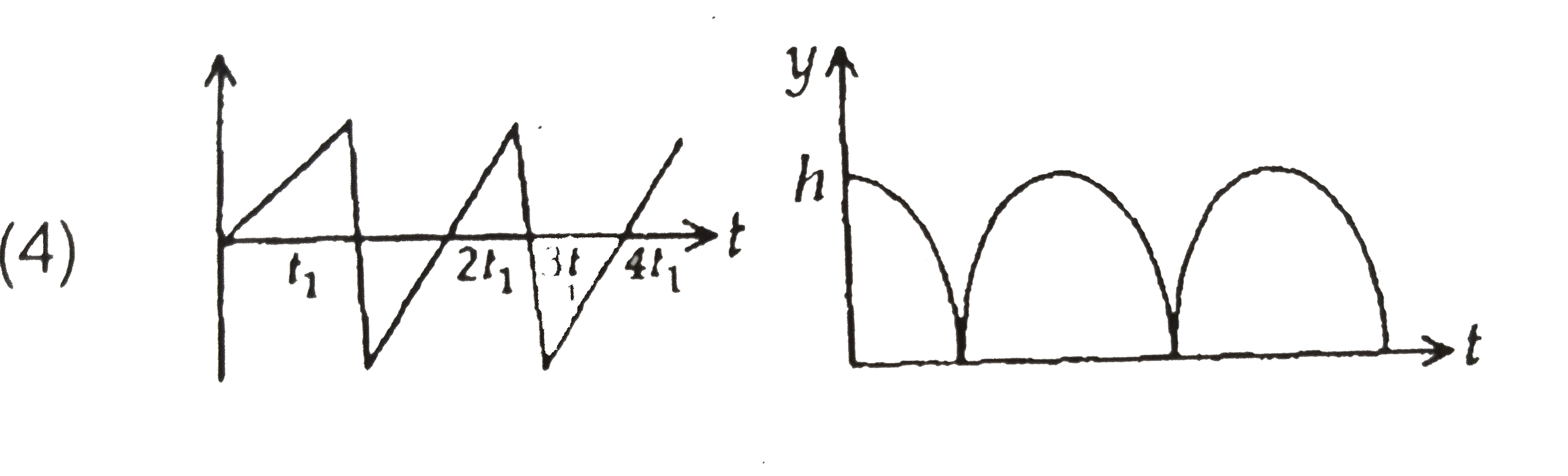
The correct Answer is:C
To solve the problem of a rubber ball falling from a height of h=4.9m onto a horizontally elastic plate, we need to determine the velocity and height of the ball as functions of time.
1. Understanding the Initial Conditions:
- The ball is dropped from rest, so its initial velocity u=0.
- The height from which it is dropped is h=4.9m.
2. Using the Kinematic Equation for Velocity:
- The equation for the velocity of an object under free fall is given by:
v=u+at
- Here, a=−g (acceleration due to gravity, negative because it is directed downwards), and g≈9.8m/s2.
- Substituting u=0:
v=0−gt=−gt
- Therefore, the velocity as a function of time is:
v(t)=−9.8t(for the downward motion)
3. Calculating the Time of Fall:
- To find the time t it takes to fall 4.9m, we use the second kinematic equation:
s=ut+12at2
- Here, s=−4.9m (since it falls down), u=0, and a=−g:
−4.9=0+12(−9.8)t2
- Simplifying gives:
−4.9=−4.9t2⇒t2=1⇒t=1s
4. Behavior During the Collision:
- Since the collision with the elastic plate is perfectly elastic, the ball will rebound with the same speed but in the opposite direction.
- Therefore, after t=1s, the velocity will be:
v=9.8m/s(upward)
5. Height as a Function of Time:
- For the upward motion after the collision, we again use the kinematic equation:
s=ut+12at2
- For the upward motion, the initial velocity u=9.8m/s and a=−g:
h(t)=4.9+9.8t−12(9.8)t2
- This will continue until the ball reaches the maximum height and then falls back down.
6. Generalizing the Motion:
- The ball will continue to bounce indefinitely, following the same pattern of falling and rebounding, maintaining the same height of 4.9m for each bounce.
Final Functions:
- Velocity as a function of time:
v(t)={−9.8tfor 0≤t<19.8(t−2n)for t in the nth bounce
- Height as a function of time:
h(t)={4.9−12gt2for 0≤t<14.9+9.8(t−2n)−12g(t−2n)2for t in the nth bounce
- The ball is dropped from rest, so its initial velocity u=0.
- The height from which it is dropped is h=4.9m.
- The equation for the velocity of an object under free fall is given by:
v=u+at
- Here, a=−g (acceleration due to gravity, negative because it is directed downwards), and g≈9.8m/s2.
- Substituting u=0:
v=0−gt=−gt
- Therefore, the velocity as a function of time is:
v(t)=−9.8t(for the downward motion)
- To find the time t it takes to fall 4.9m, we use the second kinematic equation:
s=ut+12at2
- Here, s=−4.9m (since it falls down), u=0, and a=−g:
−4.9=0+12(−9.8)t2
- Simplifying gives:
−4.9=−4.9t2⇒t2=1⇒t=1s
- Since the collision with the elastic plate is perfectly elastic, the ball will rebound with the same speed but in the opposite direction.
- Therefore, after t=1s, the velocity will be:
v=9.8m/s(upward)
- For the upward motion after the collision, we again use the kinematic equation:
s=ut+12at2
- For the upward motion, the initial velocity u=9.8m/s and a=−g:
h(t)=4.9+9.8t−12(9.8)t2
- This will continue until the ball reaches the maximum height and then falls back down.
- The ball will continue to bounce indefinitely, following the same pattern of falling and rebounding, maintaining the same height of 4.9m for each bounce.
- Velocity as a function of time:
v(t)={−9.8tfor 0≤t<19.8(t−2n)for t in the nth bounce
- Height as a function of time:
h(t)={4.9−12gt2for 0≤t<14.9+9.8(t−2n)−12g(t−2n)2for t in the nth bounce
Topper's Solved these Questions
Similar Questions
A ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 34, the ball will strike second time with the plane after
View SolutionA ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 34, the ball will strike second time with the plane after
View Solution
Knowledge Check
A ball falls under gravity from a height of 10 m with an initial downward velocity u. It collides with the ground, losses 50% of its energy in collision and then rises back to the same height. The initial velocity u is
A7ms−1B25ms−1C14ms−1D28ms−1
A ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at

View SolutionA metal ball falls from a height of 1m on to a steel plate and jumps upto a height of 81 cm. The coefficient of restitution of the ball and steel plate is
View SolutionA ball is thrown vertically downwards from a height of 20m with an intial velocity v0. It collides with the ground, loses 50% of its energy in collision and rebounds to the same height. The intial velocity v0 is (Take, g =10 ms−2)
View SolutionA ball is let fall from a height h0. There are n collisions with the earth. If the velocity of rebound after n collisions is vn and the ball rises to a height hn then coefficient of restitution e is given by
View SolutionA ball is let fall from a height h0. There are n collisions with the earth. If the velocity of rebound after n collision is vn and the ball rises to a height hn then coefficient of restitution e is given by
View SolutionA ball is dropped from height 'H' onto a horizontal surface. If the coefficient of restitution is 'e' then the total time after which it comes to rest is
View SolutionA ball is dropped from height 'H' onto a horizontal surface. If the coefficient of restitution is 'e' then the total time after which it comes to rest is
View Solution
