The anode vollage of a photocell is kept fixed . The wavelength λof the light falling on the cathode varies as follows
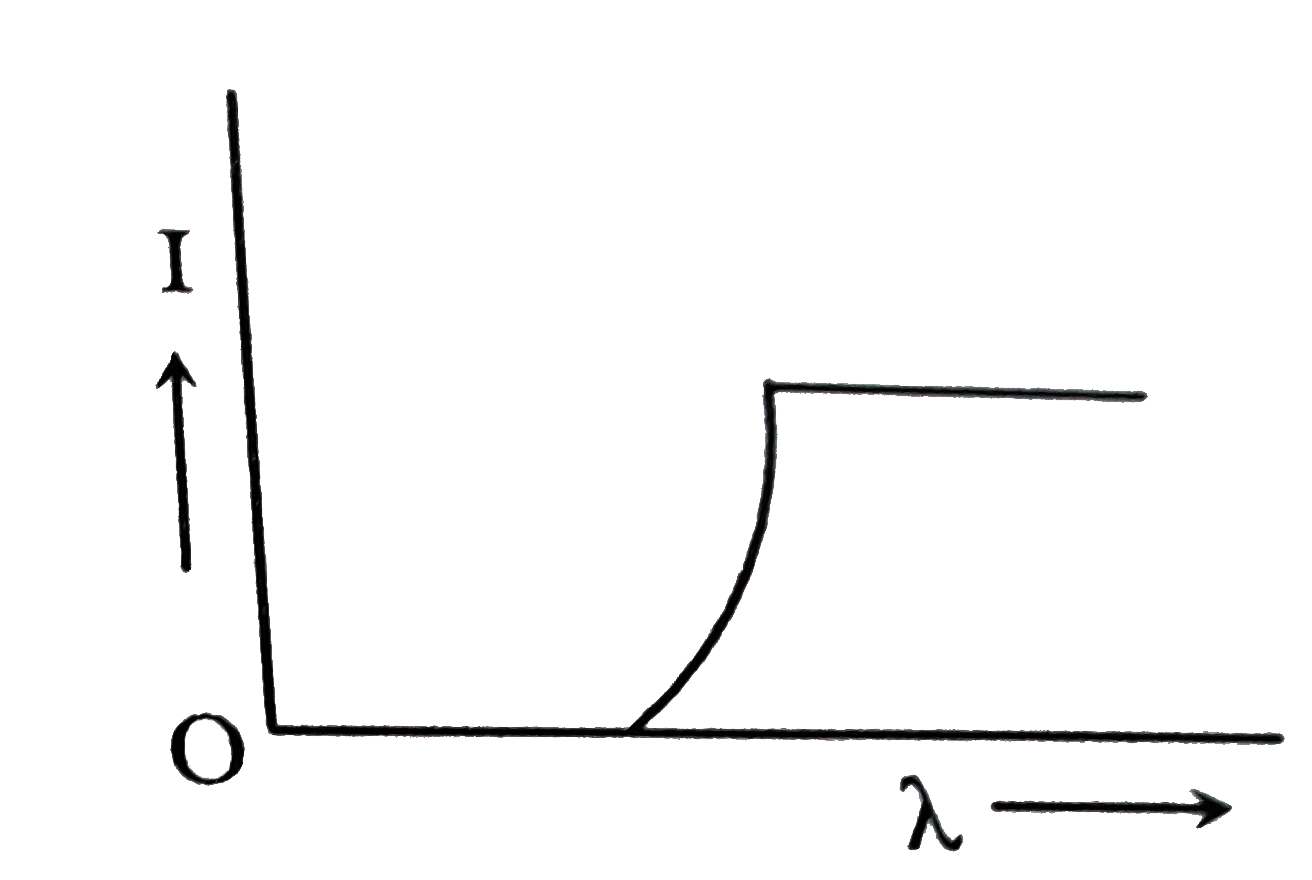
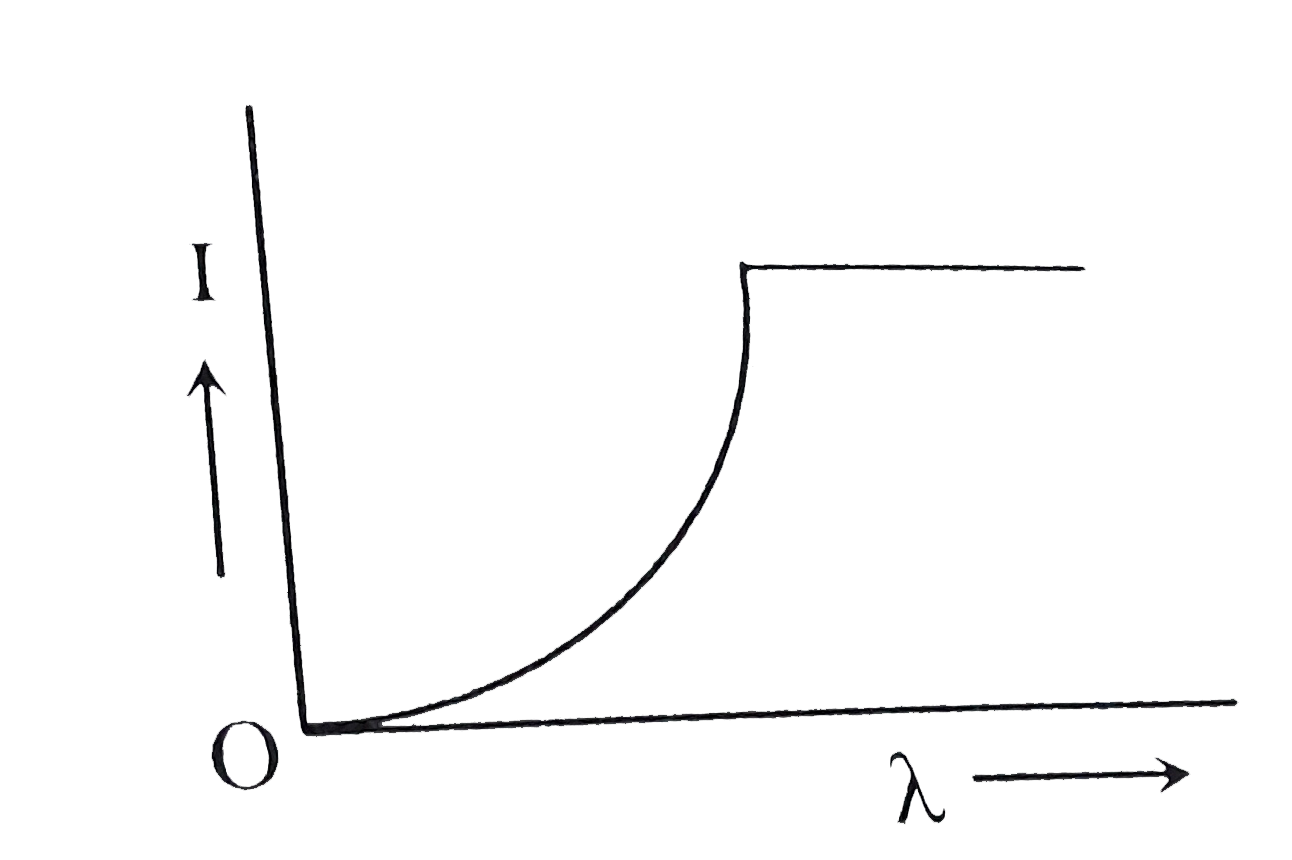
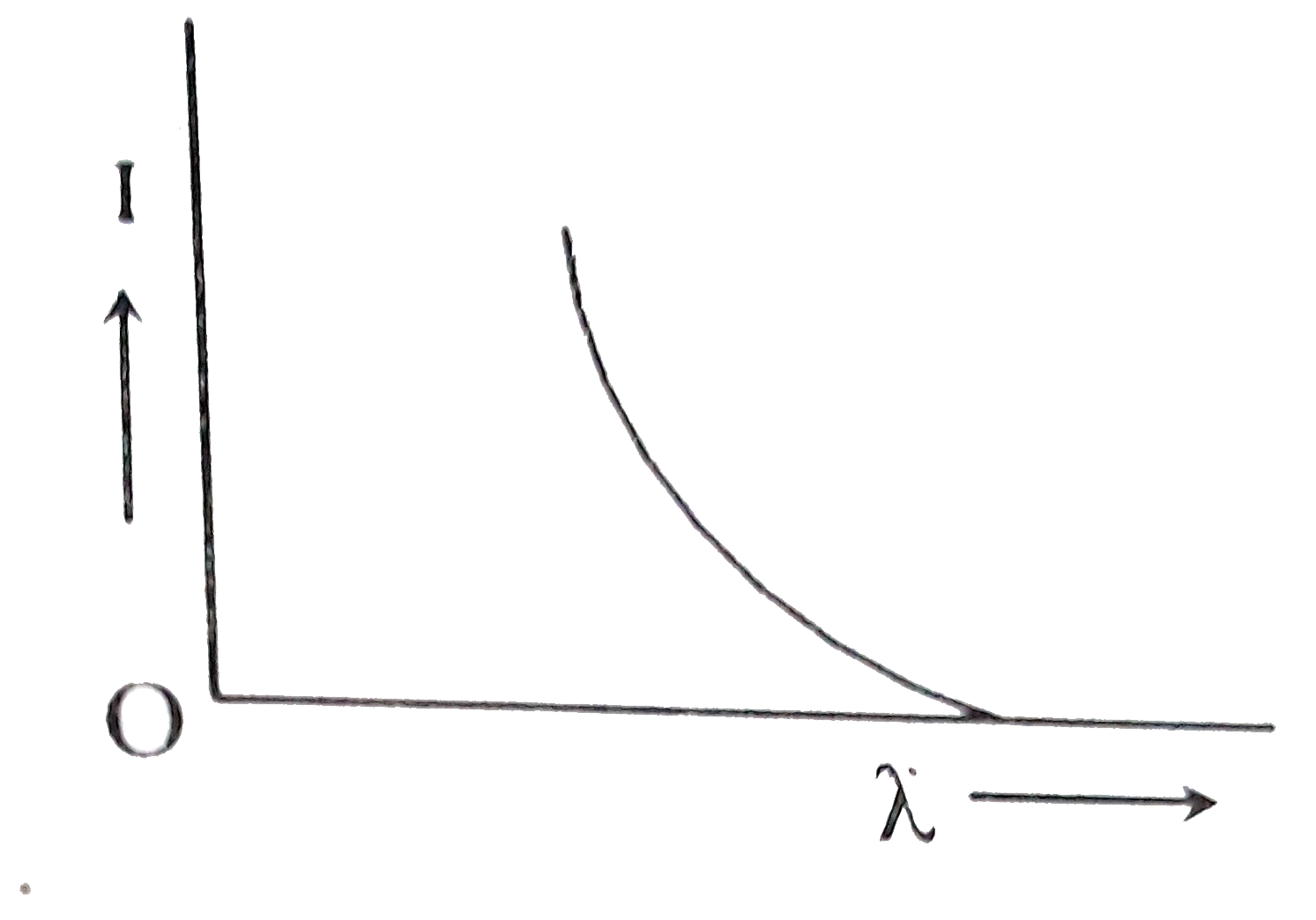
The correct Answer is:C
To solve the problem, we need to analyze how the current in a photocell varies with the wavelength of light falling on the cathode. Here’s the step-by-step solution:
Step 1: Understand the relationship between current and intensity
The current (I) in a photocell is directly proportional to the intensity (I) of the light falling on the cathode. This can be expressed as:
I∝I
Step 2: Relate intensity to wavelength
The intensity of light is defined as the energy per unit time per unit area. The energy of a photon is given by the equation:
E=hcλ
where:
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the light.
Step 3: Express intensity in terms of wavelength
If we consider the intensity (I) to be proportional to the energy, we can write:
I∝1λ
This indicates that as the wavelength increases, the intensity decreases.
Step 4: Relate current to wavelength
Since the current is directly proportional to the intensity, we can conclude:
I∝1λ
This means that the current is inversely proportional to the wavelength of the light falling on the cathode.
Step 5: Conclusion
From our analysis, we find that:
- If the wavelength (λ) increases, the current (I) decreases.
- Conversely, if the wavelength decreases, the current increases.
Thus, the correct answer is that the current is inversely proportional to the wavelength.
Final Answer:
The current in the photocell is inversely proportional to the wavelength of the light falling on the cathode.
---
The current (I) in a photocell is directly proportional to the intensity (I) of the light falling on the cathode. This can be expressed as:
I∝I
The intensity of light is defined as the energy per unit time per unit area. The energy of a photon is given by the equation:
E=hcλ
where:
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the light.
If we consider the intensity (I) to be proportional to the energy, we can write:
I∝1λ
This indicates that as the wavelength increases, the intensity decreases.
Since the current is directly proportional to the intensity, we can conclude:
I∝1λ
This means that the current is inversely proportional to the wavelength of the light falling on the cathode.
From our analysis, we find that:
- If the wavelength (λ) increases, the current (I) decreases.
- Conversely, if the wavelength decreases, the current increases.
The current in the photocell is inversely proportional to the wavelength of the light falling on the cathode.
Topper's Solved these Questions
Similar Questions
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
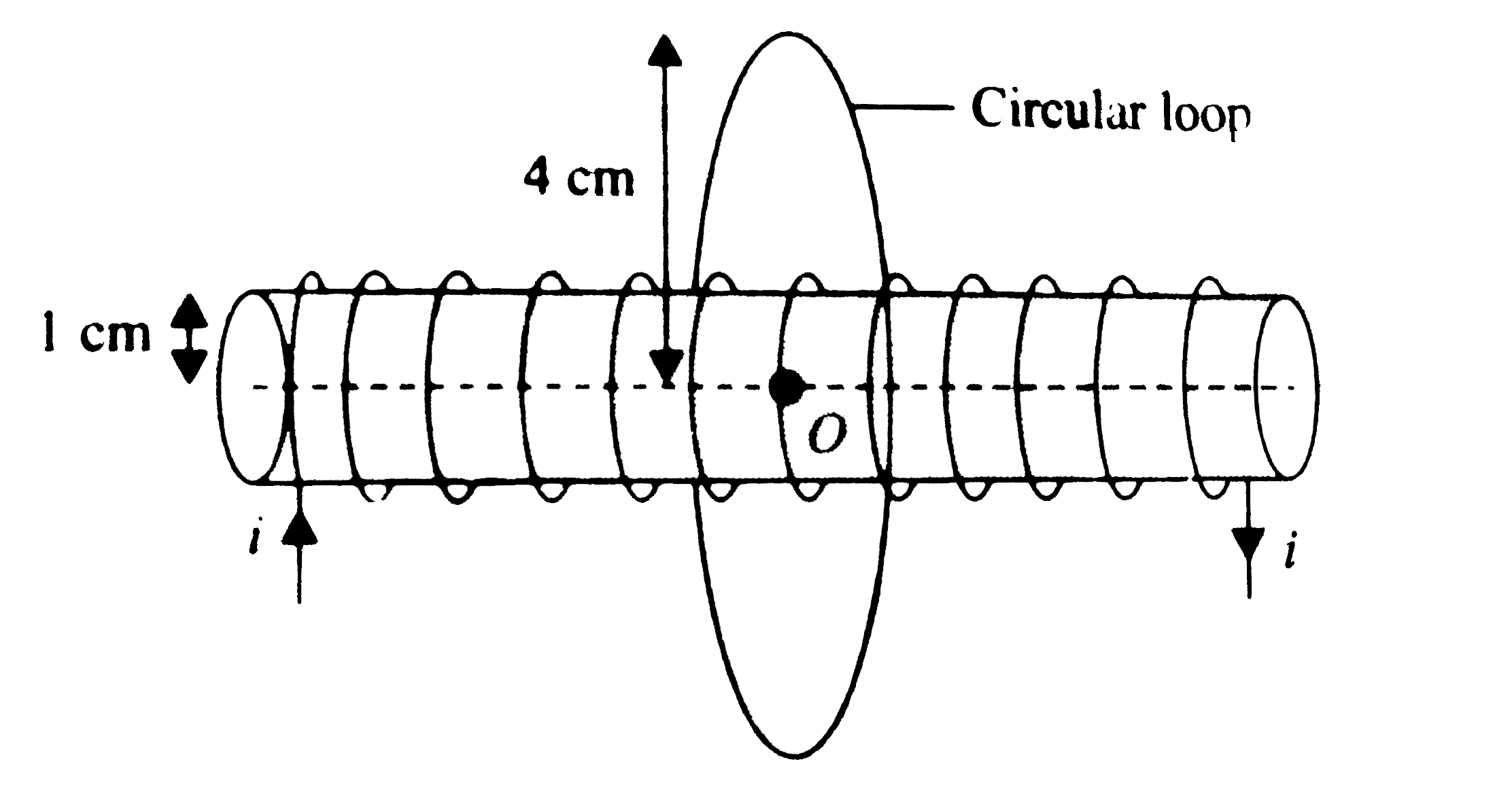
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionThe stopping potential in a photoelectric experiment is linearly related to the inverse of the wavelength (1λ) of the light falling on the cathode. The potential difference applied across an X-ray tube is linearly related to the inverse of the cutoff wavelength (1λ) of the X-ray emitted. Show that the slopes of the lines in the two cases are equal and find its value.
View Solution
Knowledge Check
In young's double slit experiment using monochromatic light of wavelengths λ, the intensity of light at a point on the screen with path difference λ is M units. The intensity of light at a point where path difference is λ/3 is
AM2BM4CM8DM16
The maximum kinetic energy of photoelectron is doubled when the wavelength of light incident on the photosensitive changes from λ1 to λ2. Deduce expression for the threshold wavelength and work function for metals in terms of λ1 and λ2
View SolutionIf λ0 is the threshold wavelength for photoelectric emission. λ wavelength of light falling on the surface on the surface of metal, and m mass of electron. Then de Broglie wavelength of emitted electron is :-
View SolutionA vacuum photocell consists of a central cathode and an anode. The internal surface is silver of work function 4.5 eV. The contact potential difference between the electrodes equals to 0.6 V. The photocell is illuminated by light of wavelength 2.3×10−7m.
a. What retrading potential difference should be applied between electrodes of the photocell for the photocurrent to drop to zero?
b. If a retarding potential of 1V is applied between electrodes at what limiting wavelength λ of light incident on the cathode will on the cathode will the photoelectric effect begin?
View SolutionElectrons are emitted from the cathode of a photocell of negligible work function, when photons of wavelength λ are incident on it. Derive the expression for the de Broglie wavelength of the electrons emitted in terms of the wavelength of the incident light
View SolutionTwo identical metal plates show photoelectric effect by a light of wavelength λA falling on plate A and λB on plate B(λA=2λB). The maximum kinetic energy is
View SolutionA source emits monochromatic light of frequency 5.5×1014 Hzat a rate of 0.1 W. Of the photons given out, 0.15% fall on the cathode of a photocell which gives a current of 6μA in an extrnal circuit.
(a) Find the enrgy of a photon.
(b) Find the number of photons leaving the source per second.
(C) Find the percentage of the photons falling on the cathode which produce photoelectrons.
View SolutionPhotoelectric work- function of a metal is 1eV. Light of wavelength λ=3000Å falls on it. The photoelectrons come out with maximum velocity
View Solution
