A green light is incident from the water to the air - water interface at the critical angle (θ). Select the correct statement.
The spectrum of visible light whose frequency is more than that of green light will come out to the air medium.
The entire spectrum of visible light will come out of the water at various angles to the normal.
The entire spectrum of visible light will come out of the water at an angle of
The spectrum of visible light whose frequency is less than that of green light will come out to the air medium.
To solve the problem of determining the correct statement regarding the behavior of green light incident from water to air at the critical angle, we can follow these steps:
Step 1: Understand the Critical Angle
The critical angle (θc) is the angle of incidence beyond which light cannot pass through the interface and is instead reflected back into the medium. For light moving from a denser medium (water) to a less dense medium (air), the critical angle can be calculated using Snell's law.
Step 2: Apply Snell's Law
Snell's law states that:
n1sin(θ1)=n2sin(θ2)
Where:
- n1 is the refractive index of water (approximately 1.33),
- n2 is the refractive index of air (approximately 1.00),
- θ1 is the angle of incidence (which will be θc at the critical angle),
- θ2 is the angle of refraction (which will be 90° at the critical angle).
At the critical angle:
n1sin(θc)=n2sin(90°)
This simplifies to:
n1sin(θc)=n2
sin(θc)=n2n1=1.001.33
Step 3: Calculate the Critical Angle
Using the above equation:
θc=sin−1(1.001.33)
Calculating this gives us the critical angle for green light transitioning from water to air.
Step 4: Analyze the Wavelength and Frequency Relationship
The refractive index (n) is related to the speed of light (c), frequency (f), and wavelength (λ) by:
n=cv=cfλ
Where:
- v is the speed of light in the medium,
- c is the speed of light in vacuum.
Since the speed of light and frequency are constant for a given monochromatic light, we can express the refractive index in terms of wavelength:
n∝1λ
Step 5: Determine the Implications for Different Colors of Light
Since the critical angle is inversely proportional to the wavelength, longer wavelengths (lower frequencies) will have a larger critical angle. Thus, for light with a wavelength greater than that of green light (like red light), it will emerge from the water at angles less than the critical angle.
Step 6: Select the Correct Statement
Based on the analysis:
- Light with a frequency lower than that of green light (longer wavelength) can exit the water at angles less than the critical angle.
- Therefore, the correct statement is that the entire spectrum of visible light whose frequency is less than that of green light will come out of the air medium.
Final Answer
The correct option is that the spectrum of visible light whose frequency is less than that of green light will come out of the air medium.
---
The critical angle (θc) is the angle of incidence beyond which light cannot pass through the interface and is instead reflected back into the medium. For light moving from a denser medium (water) to a less dense medium (air), the critical angle can be calculated using Snell's law.
Snell's law states that:
n1sin(θ1)=n2sin(θ2)
Where:
- n1 is the refractive index of water (approximately 1.33),
- n2 is the refractive index of air (approximately 1.00),
- θ1 is the angle of incidence (which will be θc at the critical angle),
- θ2 is the angle of refraction (which will be 90° at the critical angle).
n1sin(θc)=n2sin(90°)
This simplifies to:
n1sin(θc)=n2
sin(θc)=n2n1=1.001.33
Using the above equation:
θc=sin−1(1.001.33)
Calculating this gives us the critical angle for green light transitioning from water to air.
The refractive index (n) is related to the speed of light (c), frequency (f), and wavelength (λ) by:
n=cv=cfλ
Where:
- v is the speed of light in the medium,
- c is the speed of light in vacuum.
n∝1λ
Since the critical angle is inversely proportional to the wavelength, longer wavelengths (lower frequencies) will have a larger critical angle. Thus, for light with a wavelength greater than that of green light (like red light), it will emerge from the water at angles less than the critical angle.
Based on the analysis:
- Light with a frequency lower than that of green light (longer wavelength) can exit the water at angles less than the critical angle.
- Therefore, the correct statement is that the entire spectrum of visible light whose frequency is less than that of green light will come out of the air medium.
The correct option is that the spectrum of visible light whose frequency is less than that of green light will come out of the air medium.
Topper's Solved these Questions
- JEE MAINSBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINSExercise:Chemistry
Explore 1 Video
- JEE MAINBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINExercise:All Questions
Explore 452 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 250 Videos
Similar Questions
For pure water Select the correct statements :
View SolutionWhen light enters from air to water, then its
View SolutionSelect the correct statement for heavy water.
View SolutionWhite light is incident from under water on the the water-air interface. If the angle of incidence is slowly increased from zero, the emergent beam coming out into the air will turn from
View SolutionA ray of light is incident at the glass-water interface at an angle i. It merges finally parallel to the surface of water. Then, the value of μg would be
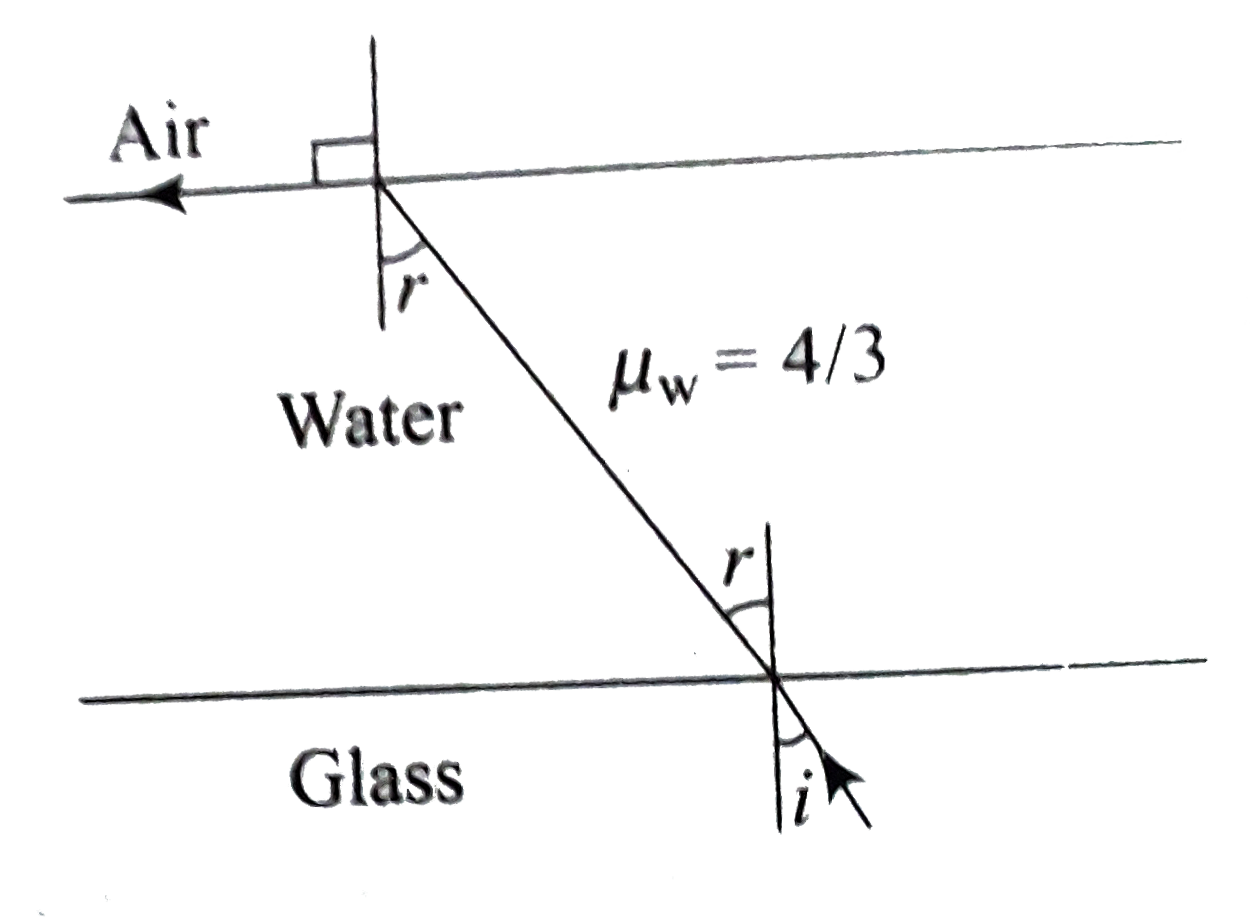
View Solution
A ray of light is incident at the glass-water interface at an angle i it emerges finnaly parallel to the surface of water, then the value of μg would be
View SolutionA ray of light enters a spherical drop of water of refractive index μ as shown in figure.
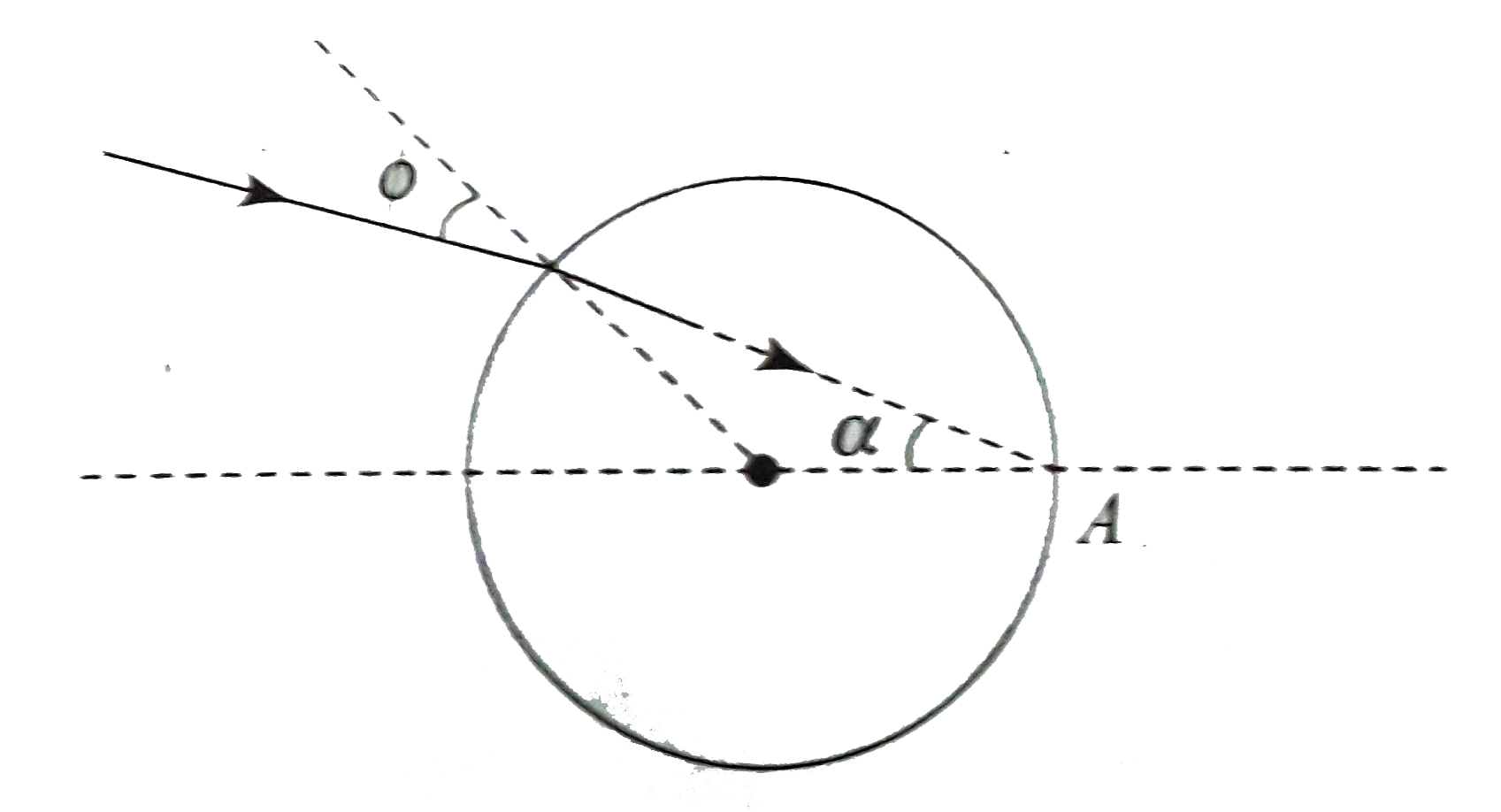
Q. Select the correct statement:
View SolutionA ray of light travelling in glass (μg=3/2) is incident on a horizontal glass-air surface at the critical angle θC. If a thin layer of water (μw=4/3) is now poured on the glass-air surface. At what angle will the ray of light emerges into water at glass-water surface?
View SolutionA ray of light travelling in glass (μ=3/2) is incident on a horizontal glass air surface at the critical angle θC. If a thin layer of water (μ=4/3) is now poured on the glass air surface, the ray of light emerge into air at the water air surface at an angle of π/k, radians find the value of k.
View SolutionIn Figure, light is incident at an angle θ which is slightly greater than the critical angle. Now, keeping the incident angle fixed a parallel slab or refractive index n3 is placed on surface AB. Which of the following statements are correct?

View Solution