A ball is dropped from a height of 320m above the ground. After every collision, the speed of ball decreases by 50%. Taking dropping point as origin, downward direction positive and collision time negligible, sketch the v-t, s-t and a-t graphs. Also calculate the total distance traveled by the ball and the total time of journey.
ωc−ωm
ωm
ωc
ωm+ωc
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the ball dropped from a height of 320 meters, considering the effects of collisions that reduce its speed by 50% after each bounce.
Step 1: Calculate the initial velocity just before the first collision
The ball is dropped from a height h=320m. Using the equation of motion:
v2=u2+2gh
where:
- u=0 (initial velocity),
- g=10m/s2 (acceleration due to gravity),
- h=320m.
Substituting the values:
v2=0+2×10×320
v2=6400⟹v=√6400=80m/s
Step 2: Calculate the height after the first collision
After the first collision, the speed of the ball decreases by 50%, so:
v1=v2=802=40m/s
Now, we calculate the height h1 it reaches after the collision using:
v2=u2+2gh1
Here, v=0 (final velocity at the peak), u=40m/s, and g=10m/s2:
0=(40)2−2×10×h1
1600=20h1⟹h1=160020=80m
Step 3: Calculate the height after the second collision
After the second collision, the speed reduces again by 50%:
v2=v12=402=20m/s
Calculating the height h2:
0=(20)2−2×10×h2
400=20h2⟹h2=40020=20m
Step 4: Calculate the height after subsequent collisions
Continuing this pattern, we find that:
- h3=h24=204=5m
- h4=h34=54=1.25m
- And so on...
Step 5: Total distance traveled
The total distance D can be calculated as:
D=320+2h1+2h2+2h3+2h4+…
This series can be expressed as:
D=320+2(h1+h2+h3+h4+…)
The heights form a geometric series:
h1+h2+h3+h4+…=80+20+5+1.25+…
This series has a first term a=80 and a common ratio r=14:
S=a1−r=801−14=8034=3203
Thus:
D=320+2×3203=320+6403=960+6403=16003m
Step 6: Total time of journey
The time taken for each segment can be calculated as follows:
- For the first fall (320 m):
t1=√2hg=√2×32010=√64=8s
- For the first rise (80 m):
t2=v1g=4010=4s
- For the second fall (80 m):
t3=4s
- For the second rise (20 m):
t4=2010=2s
Continuing this pattern, the total time can be calculated as:
T=8+4+4+2+2+1+0.5+…
This series also forms a geometric series:
T=8+8+4+2+1+0.5+…
The sum of the series is:
T=8+8(12+14+18+…)=8+8⎛⎝121−12⎞⎠=8+8=24s
Final Results
- Total distance traveled by the ball: 16003m
- Total time of journey: 24s
The ball is dropped from a height h=320m. Using the equation of motion:
v2=u2+2gh
where:
- u=0 (initial velocity),
- g=10m/s2 (acceleration due to gravity),
- h=320m.
v2=0+2×10×320
v2=6400⟹v=√6400=80m/s
After the first collision, the speed of the ball decreases by 50%, so:
v1=v2=802=40m/s
Now, we calculate the height h1 it reaches after the collision using:
v2=u2+2gh1
Here, v=0 (final velocity at the peak), u=40m/s, and g=10m/s2:
0=(40)2−2×10×h1
1600=20h1⟹h1=160020=80m
After the second collision, the speed reduces again by 50%:
v2=v12=402=20m/s
Calculating the height h2:
0=(20)2−2×10×h2
400=20h2⟹h2=40020=20m
Continuing this pattern, we find that:
- h3=h24=204=5m
- h4=h34=54=1.25m
- And so on...
The total distance D can be calculated as:
D=320+2h1+2h2+2h3+2h4+…
This series can be expressed as:
D=320+2(h1+h2+h3+h4+…)
The heights form a geometric series:
h1+h2+h3+h4+…=80+20+5+1.25+…
This series has a first term a=80 and a common ratio r=14:
S=a1−r=801−14=8034=3203
Thus:
D=320+2×3203=320+6403=960+6403=16003m
The time taken for each segment can be calculated as follows:
- For the first fall (320 m):
t1=√2hg=√2×32010=√64=8s
- For the first rise (80 m):
t2=v1g=4010=4s
- For the second fall (80 m):
t3=4s
- For the second rise (20 m):
t4=2010=2s
Continuing this pattern, the total time can be calculated as:
T=8+4+4+2+2+1+0.5+…
This series also forms a geometric series:
T=8+8+4+2+1+0.5+…
The sum of the series is:
T=8+8(12+14+18+…)=8+8⎛⎝121−12⎞⎠=8+8=24s
- Total distance traveled by the ball: 16003m
- Total time of journey: 24s
Topper's Solved these Questions
Similar Questions
A ball is dropped from a height of 10 m. If the energy of the ball reduces by 40% after striking the ground, how much high can the ball bounce back ? (g=10m/s2)
View SolutionA ball is dropped from a height of 19.6 m above the ground. It rebounds from the ground and raises itself up to the same height. Take the starting point as the origin and vertically downward as the positive X-axis. Draw approximate plots of x versus t, v versus t and a versus t. Neglect the small interval during which the ball was in contact with the ground.
View SolutionA ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View SolutionA ball is dropped from a height of 80 m on a floor. At each collision, the ball loses half of its speed. Plot the speed-time graph and velocity-time graph of its motion till two collisions With the floor. [Take g=10m/s2]
View Solution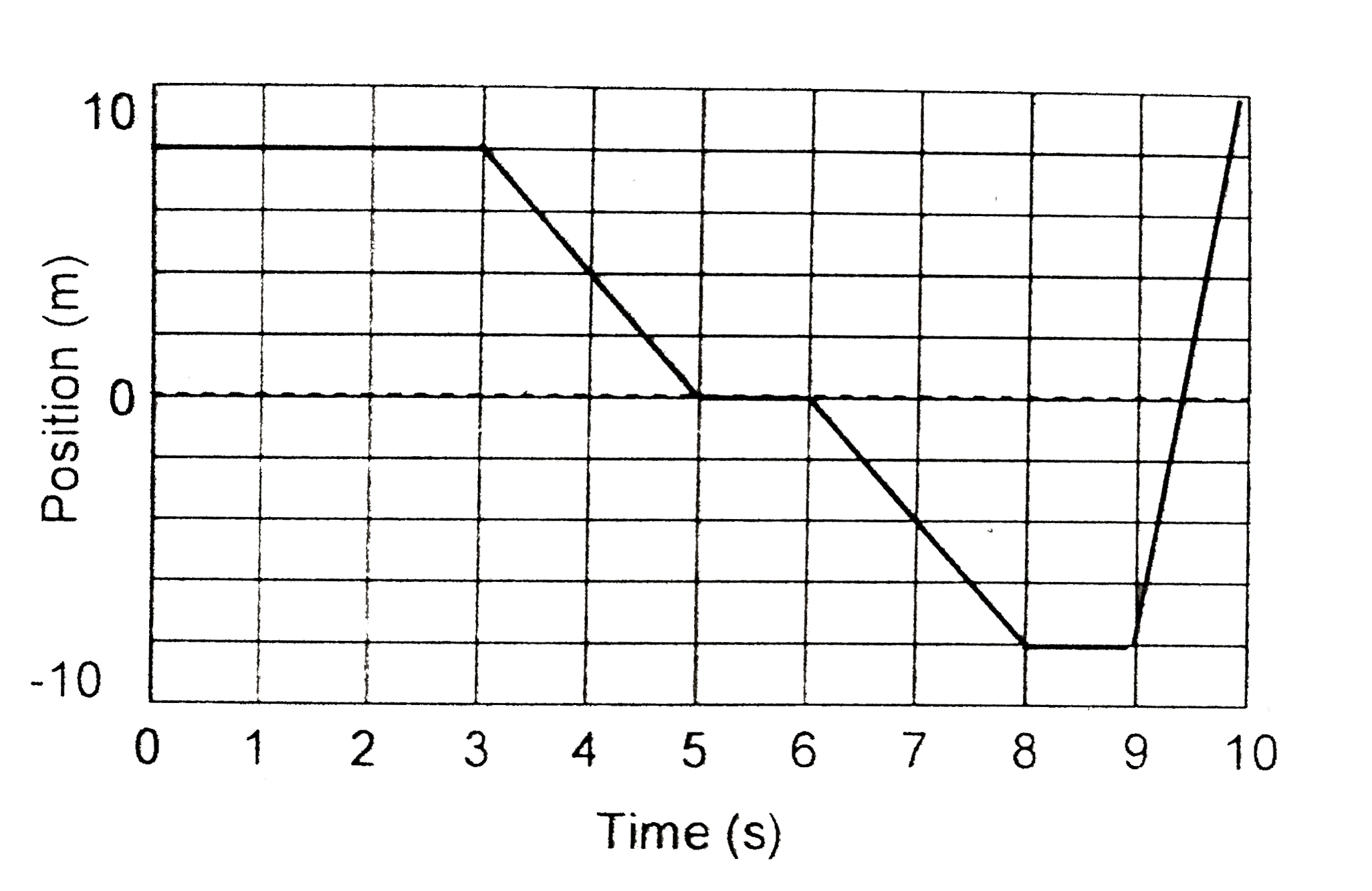
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?
View SolutionA ball is dropped from a height of 45m from the ground. The coefficient of restitution between the ball and the ground is 23. What is the distance travelled by the ball in 4th second of its motion. Assume negligible time is spent in rebounding. Let g=10ms2
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
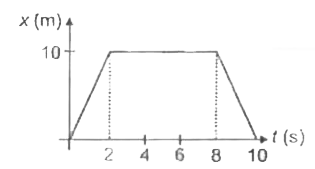
View SolutionThe speed of a train increases at a constant rate α from zero to v and then remains constant for an interval and finally decreases to zero at a constant rate β. The total distance travelled by the train is l. The time taken to complete the journey is t. Then,
View SolutionAn object is dropped from a height h from the ground. Every time it hits the ground it looses 50% of its kinetic energy. The total distance covered as t→∞ is -
View SolutionA ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
View Solution
