The maximum velocity of electrons emitted from a metal surface is v. What would be the maximum velocity if the frequency of incident lightis increased by a factor of 4?
more than √3 v
equal to √3 v
v
less than √3 v
The correct Answer is:B
To solve the problem, we need to apply the principles of the photoelectric effect, specifically Einstein's equation for the kinetic energy of emitted electrons.
1. Understanding the Photoelectric Effect:
According to Einstein's equation, the maximum kinetic energy (K.E.) of the emitted electrons can be expressed as:
K.E.=hf−ϕ
where h is Planck's constant, f is the frequency of the incident light, and ϕ is the work function of the metal.
2. Initial Condition:
Let the initial frequency of the incident light be f. The maximum kinetic energy of the emitted electrons is given as:
K.E.=12mv2=hf−ϕ
where v is the maximum velocity of the emitted electrons.
3. New Condition with Increased Frequency:
Now, if the frequency of the incident light is increased by a factor of 4, the new frequency becomes:
f′=4f
The new maximum kinetic energy can be expressed as:
K.E.′=hf′−ϕ=h(4f)−ϕ=4hf−ϕ
4. Relating the Kinetic Energies:
For the new maximum velocity v′, we can write:
K.E.′=12mv′2=4hf−ϕ
5. Setting Up the Equations:
We now have two equations:
- For the initial condition:
12mv2=hf−ϕ(1)
- For the new condition:
12mv′2=4hf−ϕ(2)
6. Dividing the Equations:
To find the relationship between v′ and v, we can divide equation (2) by equation (1):
mv′2mv2=4hf−ϕhf−ϕ
Simplifying gives:
v′2v2=4hf−ϕhf−ϕ
7. Finding the Maximum Velocity:
Let’s denote C=ϕhf. Then we can rewrite the equation:
v′2v2=4−C1−C
Taking the square root on both sides gives:
v′v=√4−C1−C
Thus, we can express v′ as:
v′=v√4−C1−C
8. Conclusion:
The maximum velocity of the emitted electrons increases when the frequency of the incident light is increased by a factor of 4. The exact relationship depends on the work function of the metal, but it is clear that v′ will be greater than v.
According to Einstein's equation, the maximum kinetic energy (K.E.) of the emitted electrons can be expressed as:
K.E.=hf−ϕ
where h is Planck's constant, f is the frequency of the incident light, and ϕ is the work function of the metal.
Let the initial frequency of the incident light be f. The maximum kinetic energy of the emitted electrons is given as:
K.E.=12mv2=hf−ϕ
where v is the maximum velocity of the emitted electrons.
Now, if the frequency of the incident light is increased by a factor of 4, the new frequency becomes:
f′=4f
The new maximum kinetic energy can be expressed as:
K.E.′=hf′−ϕ=h(4f)−ϕ=4hf−ϕ
For the new maximum velocity v′, we can write:
K.E.′=12mv′2=4hf−ϕ
We now have two equations:
- For the initial condition:
12mv2=hf−ϕ(1)
- For the new condition:
12mv′2=4hf−ϕ(2)
To find the relationship between v′ and v, we can divide equation (2) by equation (1):
mv′2mv2=4hf−ϕhf−ϕ
Simplifying gives:
v′2v2=4hf−ϕhf−ϕ
Let’s denote C=ϕhf. Then we can rewrite the equation:
v′2v2=4−C1−C
Taking the square root on both sides gives:
v′v=√4−C1−C
Thus, we can express v′ as:
v′=v√4−C1−C
The maximum velocity of the emitted electrons increases when the frequency of the incident light is increased by a factor of 4. The exact relationship depends on the work function of the metal, but it is clear that v′ will be greater than v.
Topper's Solved these Questions
Similar Questions
The maximum velocity of electrons emitted from a metal surface is v when the frequecny of light falling on it is f. The maximum velocity when the frequency becomes 4f is
View SolutionThe maximum kinetic energy of photoelectrons emitted from a metal surface increses from 0.4 eV to 1.2 eV when the frequency of the incident radiation is increased by 40% . What is the work function (in eV) of the metal surface?
View SolutionThe maximum velocity of the photoelectrons emitted from the surface is v when light of frequency n falls on a metal surface. If the incident frequency is increased to 3n, the maximum velocity of the ejected photoelectrons will be
View SolutionThe photo-electrons emitted from a surface of sodium metal are such that
View SolutionThe photo-electrons emitted from a surface of sodium metal are such that
View SolutionWhat should be the maximum velocity of an electron orbiting around a hydrogen nucleus
View SolutionWhat should be the maximum velocity of an electron orbiting around a hydrogen nucleus
View SolutionWhen a high frequency electromagnetic radiation is incident on a metallic surface, electrons are emitted from the surface. Energy of emitted photoelectrons depends only on the frequency of incident electromagnetic radiation and the number of emitted electrons depends only on the intensity of incident light.
Einstein's protoelectron equation [Kmax=hv−ϕ} correctly explains the PE, where υ= frequency of incident light and ϕ= work function.
Q. The slope of the graph between stopping potential and frequency is [here h is the Planck's constant and e is the charge of an electron] is
View Solution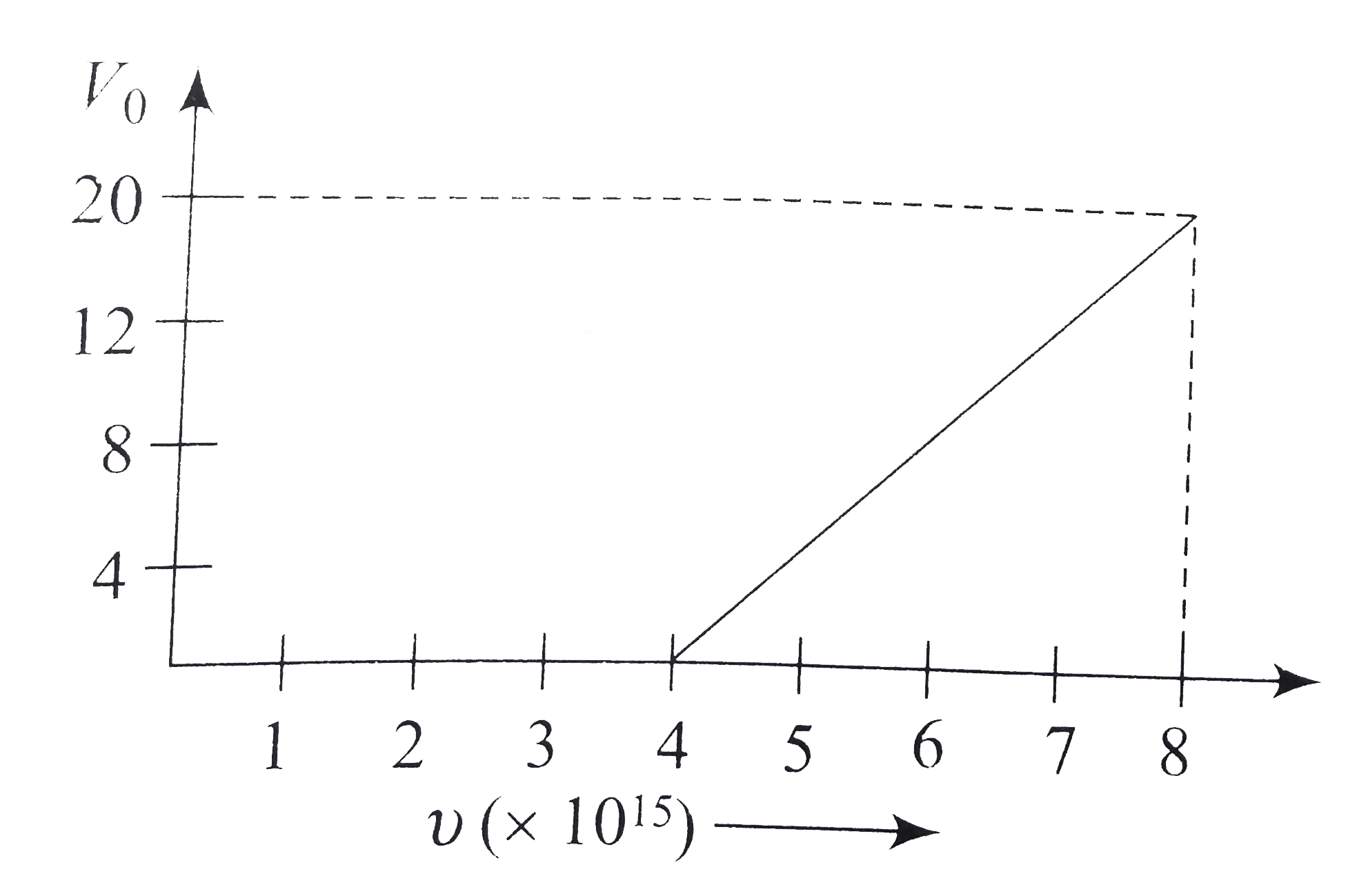
When a high frequency electromagnetic radiation is incident on a metallic surface, electrons are emitted from the surface. Energy of emitted photoelectrons depends only on the frequency of incident electromagnetic radiation and the number of emitted electrons depends only on the intensity of incident light.
Einstein's protoelectron equation [Kmax=hv−ϕ] correctly ecplains the PE, where υ= frequency of incident light and ϕ= work function.
Q. For photoelectric effect in a metal, the graph of the stopping potential V0 (in volt) versus frequency υ (in hertz) of the incident radiation is shown in Fig. The work function of the metal (in eV) is.
View SolutionThe threshold frequency for certain metal is v0. When light of frequency 2v0 is incident on it, the maximum velocity of photoelectrons is 4×106ms−1. If the frequency of incident radiation is increaed to 5v0, then the maximum velocity of photoelectrons will be
View Solution
