For a reaction, A(g)→A(l),ΔH=−3RT
The correct statement for the reaction is :
ΔH=ΔU=0
|ΔH|<|ΔU|
|ΔH|>|ΔU|
ΔH=ΔU≠0
The correct Answer is:C
To solve the problem, we need to analyze the given reaction and the relationships between the enthalpy change (ΔH) and the internal energy change (ΔU).
1. Understanding the Reaction:
The reaction given is:
A(g)→A(l)
This indicates that one mole of gas A is converting into liquid A.
2. Given Data:
The change in enthalpy (ΔH) for this reaction is given as:
ΔH=−3RT
3. Using the Thermodynamic Relationship:
We know the relationship between enthalpy change and internal energy change:
ΔH=ΔU+PΔV
where P is the pressure and ΔV is the change in volume.
4. Calculating Change in Volume (ΔV):
Since we are converting from gas to liquid, the volume of the gas will decrease significantly. For one mole of gas turning into a liquid, we can consider:
Δng=nproducts−nreactants=0−1=−1
Thus, the change in volume (ΔV) is negative.
5. Relating ΔH and ΔU:
From the ideal gas law, we can express PΔV as:
PΔV=ΔngRT
Substituting Δng=−1:
PΔV=−RT
Now, substituting this into the equation for ΔH:
ΔH=ΔU−RT
6. Substituting the Value of ΔH:
Now we substitute the value of ΔH:
−3RT=ΔU−RT
Rearranging gives:
ΔU=−3RT+RT=−2RT
7. Comparing ΔH and ΔU:
Now we have:
ΔH=−3RTandΔU=−2RT
To compare the magnitudes:
|ΔH|=3RTand|ΔU|=2RT
Therefore, we find that:
|ΔH|>|ΔU|
8. Conclusion:
The correct statement for the reaction is that the magnitude of ΔH is greater than the magnitude of ΔU.
Final Answer:
The correct statement for the reaction is:
The magnitude of ΔH is greater than the magnitude of ΔU.
---
The reaction given is:
A(g)→A(l)
This indicates that one mole of gas A is converting into liquid A.
The change in enthalpy (ΔH) for this reaction is given as:
ΔH=−3RT
We know the relationship between enthalpy change and internal energy change:
ΔH=ΔU+PΔV
where P is the pressure and ΔV is the change in volume.
Since we are converting from gas to liquid, the volume of the gas will decrease significantly. For one mole of gas turning into a liquid, we can consider:
Δng=nproducts−nreactants=0−1=−1
Thus, the change in volume (ΔV) is negative.
From the ideal gas law, we can express PΔV as:
PΔV=ΔngRT
Substituting Δng=−1:
PΔV=−RT
Now, substituting this into the equation for ΔH:
ΔH=ΔU−RT
Now we substitute the value of ΔH:
−3RT=ΔU−RT
Rearranging gives:
ΔU=−3RT+RT=−2RT
Now we have:
ΔH=−3RTandΔU=−2RT
To compare the magnitudes:
|ΔH|=3RTand|ΔU|=2RT
Therefore, we find that:
|ΔH|>|ΔU|
The correct statement for the reaction is that the magnitude of ΔH is greater than the magnitude of ΔU.
The correct statement for the reaction is:
The magnitude of ΔH is greater than the magnitude of ΔU.
Topper's Solved these Questions
Similar Questions
For the reaction
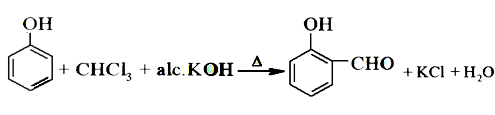
The correct statement regarding above reaction is
View SolutionFor the reaction : N2(g)+3H2(g)⇔2NH3(g), ΔH=−ve, the correct statement is :
View SolutionFor the given reaction 2A(g)+ B(g) ⇔ C(g) , ΔH = x kJ which of the following favour the reactants ?
View SolutionThe ΔH∘ for the reaction
H2(g)+I2(g)→2HI(g)
is +53.6 kJ. Mention whether the reaction is exothermic or endothermic and calculate the standard heat of formation of HI.
View SolutionIf ΔG∘>0 for a reaction then :
View SolutionFor the gas-phase reaction, 2NO ⇔N2+O2:ΔH=−43.5 keal. Which one of the following is false for the reaction N2(g)+O2(g)⇔2NO(g)
View SolutionFor the reaction,
H2O2+2H++3l−→l−3+2H2O
select the correct statement
View SolutionFor a reverisble reaction A⇔B, if pre-exponential factor is same for both forward and backward reactions, show that keq=e−ΔH/RT, where ΔH is the heat of reaction.
View SolutionConisder the chemical reaction
N2(g)+3H2(g)→2NH3(g)
The rate of this reaction can be expressed in terms of time derivatives of the concentration of N2(g),H2(g), or NH3(g). Identify the correct relationship among the rate expresisons.
View SolutionFor the reaction, A(s)+3B(g)→4C(g)+d(l)ΔHandΔU are related as :
View Solution
